JEE Advanced (One or More Correct Option): Conic Sections | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Equations of the circles concentric with the circle x2 –y2 + 2x – 4y = 0 and touching the circle x2 + y2 + 2x = 1, will be
(a) x2 + y2 – 2x – 4y = 0
(b) x2 + y2 – 2x – 4y + 3 = 0
(c) x2 + y2 – 2x – 4y – 13 = 0
(d) x2 + y2 – 2x – 4y – 1 = 0
Correct Answer is option (b, c)
Centre of the circle must be radius = r. ≡ (1, 2)
Centre of second circle = (-1, 0), radius = √2 .
The distance between centres = 2√2 which must be either r + 2 or r1 – r2. ⇒ r = √2 or 3√2
Q.2. An equation of a circle which touches the y-axis at (0, 2) and cuts off an intercept 3 from the x-axis is
(a) x2 + y2 + 4x -5y + 4 = 0
(b) x2 + y2 + 5x - 4y + 4 = 0
(c) x2 + y2 -5x - 4y + 4 = 0
(d) x2 + y2 -5x + 4y + 4 = 0
Correct Answer is option (b, c)
As the required circle touches the y-axis at (0, 2), let its equation be (x - α)2 + (y – 2)2 = α2 or x2 + y2 – 2αx - 4y + 4 = 0.
This circle meets the x-axis at the points where x2 – 2αx + 4 = 0, which gives two values of x, say x1, x2, such that x1 + x2 = 2α and x1x2 = 4. Now, we are given that |x1 – x2| = 3.
Hence the equation of the required circle is x2 + y2 ± 5x –4y + 4 = 0.
Q.3. Two circles, each of radius 5 units, touch each other at (1, 2). If the equation of their common tangent is 4x + 3y = 10, then the equations of the circles are
(a) x2 + y2 + 10x + 10y + 25 = 0
(b) x2 + y2 – 10x – 10y + 25 = 0
(c) x2 + y2 + 6x + 2y – 15 = 0
(d) x2 + y2 – 6x – 2y + 15 = 0
Correct Answer is option (b, c)
4x + 3y = 10 is equation of common tangent at P(1, 2). Equation of normal at P is
as slope of 4x + 3y = 10 is
Now radius = 5
Now put this in (2), β = 5, 1. Thus (α, (B) = (5, 5), (-3, -1).Equation of circle is (x – 5)2 + (y – 5)2 = 52 and (x + 3)2 + (y + 1)2 = 52
⇒ x2 + y2 – 10x – 10y + 25 = 0 and x2 + y2 + 6x + 2y – 15= 0 .
Q.4. C1: x2 + y2 = 25, C2 : x2 + y2 – 2x – 4y – 7 = 0 be two circles intersecting at the points A and B
(a) Equation of common chord must be x + 2y – 9 = 0
(b) Equation of common chord must be x + 2y + 7 = 0.
(c) Tangents at A and B to the circle C1 intersect at 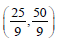
(d) Tangents at A and B to the circle C1 intersect at (1, 2).
Correct Answer is option (a, c)
Let tangents intersect at (α, (B) then the line joining the two points at which tangents are drawn is
(i) common chord of C1 and C2 is C1 - C2 = 0 ⇒ 2x + 4y -18 = 0.
(ii) chord of contact when tangents are drawn from (α, (B) to C1
⇒ Equations 2x + 4y – 18 = 0 and αx + βy – 25 = 0 must be identical on comparing,
we get,
Q.5. The equation of a tangent to the circle x2 + y2 = 25 passing through the point (-2, 11) is
(a) 4x + 3y = 25
(b) 7x – 24y = 320
(c) 3x + 4y = 38
(d) 24x – 7y + 125 = 0
Correct Answer is option (a, d)
Let the tangent be y - 11 = m(x + 2)
Its distance from centre (0, 0) should be the radius 5.
Q.6. The line y = mx + c intersects the circle x2 + y2 = r2 at two real distinct points if
(a) 
(b) 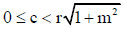
(c) 
(d) 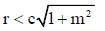
Correct Answer is option (a, b)
The x-coordinates of the points of intersection of the line y= mx + c and the circle x2 + y2 = r2 are given by x2 + (mx +(C)2 = r2
or (1 + m2)x2 + 2mcx + c2 – r2 = 0 ….(i)
which, being quadratic in x, gives two values of x and hence two points of intersection. These points will be real and distinct if the discriminant of (i) is positive i.e.,
4m2c2 – 4(1 + m2) (c2 – r2) > 0 ⇒ c2 < r2 (1 + m2)
⇒
Q.7. Equation of common tangent(s) to the circles x2 + y2 - 6x = 0 , x2+ y2 + 2x = 0 is (are)
(a) x = 0
(b) y = 0
(c) √3y = x +3
(d) x + y√3 +3 = 0
Correct Answer is option (a, c, d)
Centre A = (3,0) centre B = (-1,0)
Radius = 3 radius = 1
C1 and C2 touch at (0,0) externally
∴ x = 0 is a tangent to both C1 and C2. The others are x ± √3y + 3 = 0 which can be easily verified.
Q.8. If the line y = x + c intersects the circle x2 + y2 = r2 in two real distinct points then
(a) -r√2 < c ≤ 0
(b) 0 ≤ c < r√2
(c) -c√2 < r
(d) r < c√2
Correct Answer is option (a, b)
Solving the line and circle simultaneously,we get x2 + (x + (C)2 = r2 ⇒ 2x2 + 2cx + c2 – r2 = 0
For real intersections
Q.9. If a chord of the circle x2 + y2 – 4x – 2y – c = 0 is trisected at the point (1/3, 1/3) and (8/3, 8/3), then
(a) Length of the chord = 7√2
(b) c = 20
(c) Radius of the circle = 25
(d) c = 25
Correct Answer is option (a, b, c)
Equation of the line joining the given points is y = x and the distance between them is
If PQ is the chord of the given circle which is trisected at these points then equation of PQ is y = x and the length of this chord isLet C(2, 1) be the centre of the
given circle and CL be the perpendicular from C to PQ, then the radius of the given circle is
Q.10. If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to the same circle, then
(a) radius of the circle = 3/4
(b) radius of the circle = 3/2
(c) centre of the circle lies on 12x – 16y + 1 = 0
(d) centre of the circle lies on 12x – 16y + 31 = 0
Correct Answer is option (a, c)
The given lines being parallel tangents to a circle, the diameter of the circle is equal to the distance between these lies, so that the required radius is
The centre of the circle lies on the line parallel to the given lines at a distance of 3/4 from each of them. So let the equation be 3x – 4y + k = 0 ..…(i)
Then,
For k=1/4 distance of (i) from the other line is 3/4.
Thus the centre lies on the line 12x – 16y + 1 = 0
Q.11. The coordinates of an end-point of the latus rectum of the parabola (y – 1)2 = 2(x + 2) are
(a) (-2, 1)
(b) (-3/2, 1)
(c) (-3/2, 2)
(d) (-3/2, 0)
Correct Answer is option (c, d)
Equation of the parabola is of the form Y2 = 4aX, where Y =y – 1, a=1/2 , X = x+2The coordinates of the end–points of the latus rectum are (a, 2(A) and (a, –2(A)
i.e., X = a ⇒ x + 2 = 1/2 ⇒ x = –3/2
Y = ± 2a ⇒ y – 1 = ± 2 × 1/2 ⇒ y = 0 or y = 2.
Q.12. Equation of the tangent to the parabola y2 = 4x which makes an angle θ with its axis is
(a) y = x tanθ + cotθ
(b) y = x tanθ + secθ
(c) x = y cotθ - cot2θ
(d) x = y cotθ + tanθ
Correct Answer is option (a, c)
Q.13. The equation of a tangent to the parabola y2 = 8x which makes an angle 45° with the line y = 3x + 5 is
(a) 2x + y + 1 = 0
(b) y = 2x + 1
(c) x – 2y + 8 = 0
(d) x + 2y – 8 = 0
Correct Answer is option (a, c)
Equation of tangent in terms of slope of y2 = 8x is y = mx + 2/m ...(i)
∴ Angle between equation (1) and y = 3x + 5 is 45°, then
⇒ Equation of tangent are 2x + y + 1 = 0 and x – 2y + 8 = 0.
Q.14. The locus of mid-point of chord of parabola x2 = 4y passing through a end point of latus rectum will be
(a) x2 = 2 (x + y - 1)
(b) x2 = 2(x - y + 1)
(c) x2 = 2 (-x + y - 1)
(d) none of these
Correct Answer is option (a, c)
Let P(h, k) be the mid-point of chord, its equation will be xh - 2(y + k) = h2 - 4k
it passes through (2, 1) on (-2, 1), so lotus of p will be x2 = 2(±x + y - 1).
Q.15. If a normal chord of y2 = 4ax subtends an angle π/2 at the vertex of the parabola then it’s slope is equal to
(a) 2
(b) √ 2
(c) 1
(d) – 1
Correct Answer is option (a, b)
Q.16. The normal y = mx - 2am - am3 to the parabola y2 = 4ax subtends a right angle at the vertex if
(a) m = 1
(b) m = √2
(c) m = -√2
(d) m = 1/√2
Correct Answer is option (b, c)
Making y2 = 4ax homogeneous with the help of y = mx -2am - am3
We get, (2m + m3) y2 - 4mx2 + 4xy = 0 ... (i)
⇒ Angle between the lines represented by equation (i) is π/2.∴ Coefficient of x2 + coefficient of y2 = 0.
⇒ 2m + m3 - 4m = 0
⇒ m2 = 2, m≠ 0⇒ m = ±√2 .
Q.17. A circle touches the parabola 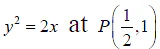 and cuts the parabola at its vertex V. If the centre of the circle is Q, then
and cuts the parabola at its vertex V. If the centre of the circle is Q, then
(a) The radius of the circle is 5/√2
(b) The radius of the circle is the maximum value of 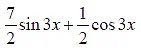
(c) Area of ΔPVQ is 15/16
(d) Slope of PQ is -2
Correct Answer is option (a, b, c)
Equation of the circle will be of the form
Where 2x - 2y +1 = 0 is tangent to parabola at
Q.18. If from P(-1, 2) tangents PA and PB are drawn to the parabola y2 = 4x then
(a) Equation of AB must be y = x – 1
(b) Length of AB must be 8
(c) Length of AB must be 4
(d) All the above
Correct Answer is option (a, b)
Equation of chord of contact is yy1 = 2a(x + x1) Now, length of the chord joining
Since, tangents intersect at (-1, 2)
Hence, length (i) is evaluated as 8,
∴ Equation of AB is y = x -1 and length of AB = 8
Q.19. Normal drawn to the parabola y2 = 4ax meet the curve again at Q such that the angle subtended by PQ at vertex is 90° then co-ordinates of P can be
(a) (a, 2a)
(b) (2a, 2√2a )
(c) (2a, -2√2a )
(d) 2a - a)
Correct Answer is option (b, c)
Q.20. A circle having its centre at (2, 3) is cut orthogonally by the parabola y2 = 4x . The possible intersection point(s) of these curves, can be
(a) (3,2 3)
(b) (2,2 2 )
(c) (1,2)
(d) (4,4)
Correct Answer is option (a,b, d)
Any tangent to the parabola y2 = 4x at (t2, 2t) is yt2 = x + t2
If it passes through the centre (2,3) of the circle, then t2 -3t + 2 = 0 ⇒t =1,2∴ The point can be (1,2) or (4,4)
|
446 docs|930 tests
|

|
Explore Courses for JEE exam
|

|














 Let C(2, 1) be the centre of the
Let C(2, 1) be the centre of the































