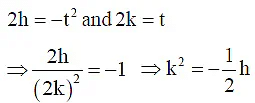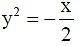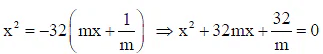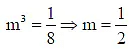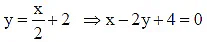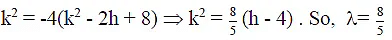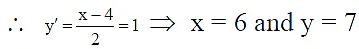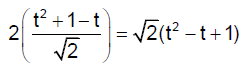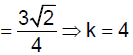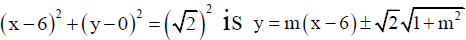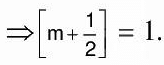Integer Answer Type Questions for JEE: Conic Section | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. A line passing through (21,30) and normal to the curve y = 2√x .If m is slope of the normal then m+6 =

Ans. 1
Equation of the normal is 3 y = mx - 2m-m³
If it pass through (21,30) we have
30 = 21m- 2m-m³ ⇒ m³ -19m+ 30 = 0
Then m = -5, 2,3
But if m= 2 or 3 then the point where the normal meets the curve will be ( am², -2am)  where the curve does not exist.
Therefore m= -5
∴ m+6 =1

Q.2. The locus of mid points of a system parallel chords with slope = 4 to the parabola 7y²=25x. is 56y=k² then k =

Ans. 5
It is locus of Mid-point of system of parallel chords.

Q.3. If L be the shortest distance between parabola y² = 100x and circle (x – 26)² + y² = 1, then 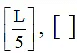 denotes the G.I.F. is

Ans. 5

Shortest distance between two non-intersecting curves occurs along a common normal.

Q.4. If any tangent to parabola y2 = 4x cut the co-ordinate axes at A and B respectively, The locus of mid point of AB is 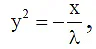 then λ is

Ans. 2
Let any tangent to parabola y² = 4x is yt = x + t²
Let R is (h, k)

Locus is

Q.5. The equation of the line touching both the parabolas y² = 4x and  x² = -32y is x - 2y + λ = 0, then λ is

Ans. 4
Equation of tangent of parabola y² = 4x is

Equation (i) is also a tangent of x² = -32y
then

Condition of tangency (D = 0)

From Equation (i), 

Q.6. Tangents are drawn from the points on the parabola y² = -8(x+4) to the parabola y2 = 4x, if local of mid point of chord of contact is again a parabola, with length of latus rectum λ, then 5λ is ....... .

Ans. 8

Let (x₁, y₁) be a point on y² = -8(x + 4)

Equation of chord of contact is

2x - y₁ y + 2x₁ = 0, if p(h, k) be its mid-point, then its equation will be

2x - ky + k² - 2h = 0

Compare both k = y₁ , 2x₁ = k² - 2h
So,

Q.7. Minimum distance between the parabolas y² – 4x – 8y + 40 = 0 and x² – 8x – 4y + 40 = 0 is√λ. Then the value of λ is

Ans. 2

Since two parabolas are symmetrical about y = x
Minimum distance is distance between tangents to the parabola and parallel to y = x.
Differentiating x² - 8x - 4y + 40 = 0 w.r.t x, we get 2x - 8 - 4y' = 0

Corresponding point on (y - 4)2 = 4(x - 6) is (7, 6) so minimum distance = 2 .

Q.8. The shortest distance between the parabolas y² = x – 1 and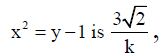
then the value of numerical quantity k must be.

Ans. 4

Since both curves are symmetrical about the line y = x distance between any pair of

points = 2(distance of (t, t² + 1) on the parabola y = x² + 1 from y – x = 0)

The minimum value of  ⇒ Minimum distance

Q. 9. If a focal chord of y² =16x is a tangent to the circle (x-6)² + y² = 2, then the positive value of the slope of this chord is

Ans. 1

Equation of parabola  y² =16x, focus (4, 0).

The equation of tangents of slope m to the circle

If this tangents pass through the focus i.e. (4,0), then
2m² = 2⇒m = ±1

∴ the positive value of m = +1.

Q.10. Circle (x - 1)² + (y - 1)² = 1 touches X and Y axis at A and B respectively. A line y = mx intersects this circle at P and Q. If area of ΔPQB is maximum then find the value of 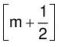.(where [.] denotes the greatest integer function).

Ans. 1
Area of  which is maximum where m = 1/√3