JEE Advanced (One or More Correct Option): Probability | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. A drawer contains red and black balls.  When two balls are drawn at random, the probability that they both are red is 1/2.  The number of balls in the drawer can be
(a) 21
(b) 11
(c) 4
(d) 3

Correct Answer is options (a, c)
Let the drawer contain p balls of which ‘m’ are red.
Probability of drawing two red balls at random is
⇒ 2m(m -10 = p (p -1) ⇒ 2m² - 2m - p² + p = 0
⇒
⇒ 1- 2p + 2p² should be an odd perfect square.
i.e., p = 21, 4 but p ≠ 3
When 3 balls out of 4 are red
15 balls out of 21 are red.

Q.2. In a gambling between Mr.  A and Mr. B a machine continues tossing a fair coin until the two consecutive throws either HT or TT are obtained for the first time.  If it is HT, Mr, A wins and if it is  TT, Mr, B wins.  Which of the following is (are) true?
(a) probability of winning Mr.A is 3/4
(b) Probability of Mr. B winning is 1/4
(c) Given first toss is head probability of Mr. A winnings is 1
(d) Given first toss is tail, probability of Mr. A winning is 1/2

Correct Answer is options (a, b, c, d)
If T comes in first toss then Mr. B can win in only one case that is TT.
⇒ Probability of Mr. B winning = 1/4
⇒ Probability of Mr.A winning = 3/4
Given first toss is head, Mr. A can win is successive tosses are T, HT, HHT, …..
Probability =
Given first toss is head, Mr.A can win is successive tosses are HT, HHT, HHHT, …..
Probability =

Q.3. If A and B are two events such that P ( A) = 1/ 2 and P ( B) = 2 / 3, then

(a) P(A ∪ B)³ 2 / 3

(b) P(A ∩ B')≤ 1/ 3
(c) 1/ 6 ≤ P(A ∩ B) ≤1/ 2
(d) 1/ 6 ≤ P (A' ∩ B) ≤ 1/ 2

Correct Answer is options (a, b, c, d)

∴ P ( A) = 0.8, P ( B) = 0.7
∴ Required probability  =
= 0.02 x  0.7 + 0.8 x 0.3 + 0.2 x 0.3 = 0.44

Q.4. An urn contains fair tickets with numbers 112, 121, 211, 222 and one ticket is drawn. Let

Ai(i = 1, 2, 3) be the event that the i^th digit of the number of ticket drawn is 1 then
(a) P(A₁) = P(A₂₎ = P(A₃) = 1/2
(b) P(A_{1 ∩} A2) = P(A₁ .P(A₂)
(c) A₁, A₂, A₃ are pairwise independent events
(d)    P(A_{1 ∩} A_{2 ∩} A₃) ≠ P(A₁ P(A₂)P(A₃)

Correct Answer is options (a, b, c, d)
P(A_{1 ∩} A₂) = 1/4
P(A₁) = 2/4
P(A₂) = 12 .
Thus, P(A_{1 ∩} A₂) = P(A₁) P(A₂).
Similarly other are true.  

Q.5. The letter of the word PROBABILITY are written down at random in a row. Let E₁ denotes the event that two I’s are together and E₂ denotes the event that two B’s are together, then
(a)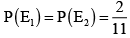
(b)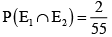
(c)
(d)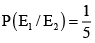

Correct Answer is options (a, b, c, d)
The total number of ways = 2n
A person is odd man out if he is alone is getting head or a tail.
The number of favourable ways = The number of ways in which there is exactly one tail (head) and the rest are heads (tails)
= ⁿC₁ + ⁿC₁ = 2n
∴
⇒ n =2^n-2 
By trial, n = 4

Q.6. Let us define the events A and B as
A: An year chosen at random contains 29 days in the February month.
B: An year chosen at random has does not contain 53 Fridays.
If P(E) denotes the probability of happening of event E then
(a)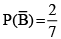
(b) P(B) = 23/28
(c)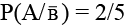
(d) P(A/(B) = 5/23

Correct Answer is options (b, c, d)
P(A) = 1/4, P(B/(A) =  = 6/7

= 23/28

Q.7. For any two random events A,B with 0 < P (A)< 1,0 < P (B)<1, which of the following is/are always true ?
(a) P(A/ B) > P( A) ⇒ P (B / A) > P (B)
(b) P(B / A) + P ( Bc / Ac )= 1
(c) P(B / A) = P ( B / Ac ) only when A,B are independent
(d) P( A / B) = P ( Ac / B ) only when A,B are mutually exclusive 

Correct Answer is options (a, c)
P A/ B > P(A)⇒ P(A ∩ B)> P(A)P(B)
⇒
(B)  is false. In the experiment of rolling a die consider A= {2, 4, 6} and B = {2, 3, 5}.
Then ( B/A ) = 1/3
P(B^c / A^c) =  1/3
(C)
⇒ [1- P( A)] P( A ∩ B) = [P(B) - P( A∩ B)] P( A)
⇒ P A ∩ B = P( A) P(B)
(D) In example (B), consider A = {2, 4, 6} and B = {3, 6} Then ( A/B ) 1/2 P(A^c/ B) = 1/2
But A ∩ B = {6} ≠  f

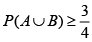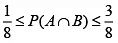 Q.8. Let A,B be two events such that  and . Then
(a)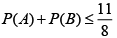
(b)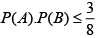
(c)
(d)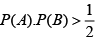

Correct Answer is options (a, c)

⇒
∴  and

Q.9. One card is missing from a pack of cards. Let A be the event that missing card is a king. Then two cards are drawn and S be the event that they are spades then -
(a)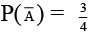
(b)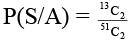
(c)
(d) P(A) = P(A/S)

Correct Answer is options (a, c)
(A)  (Event missing card is not a spade)
(B)  (Only 12 spades left when missing card is spade)
(C)  =
= 11/50

Q.10. If 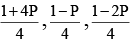 are probabilities of three mutually exclusive and exhaustive events, then the possible value of P belongs to set -
(a) (0, 2/3)
(b) [0, 1/2]
(c) [-1/4, 1/2]
(d) [-2/3, 2/3]

Correct Answer is options (b, c)

The events are mutually exclusive so,

⇒ - 3 ≤  P ≤  1
Intersection of all four intervals of P
We get