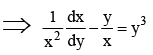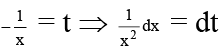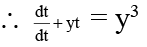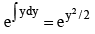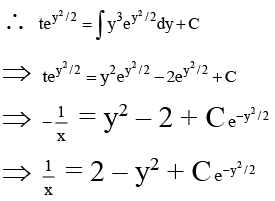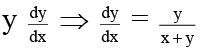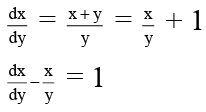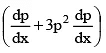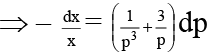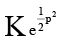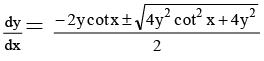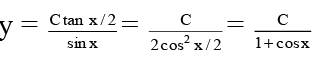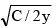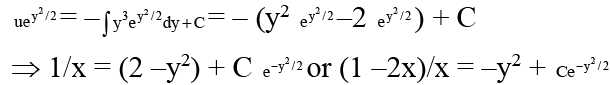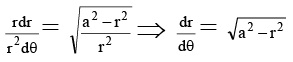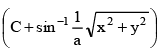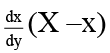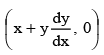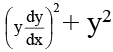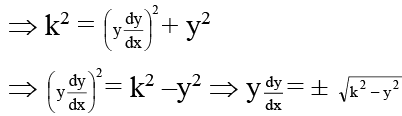JEE Advanced (One or More Correct Option): Differential Equations | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. The solution (s) of 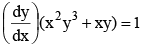is/are-

(a) 1/x = 2 – y² + C_e^-y2/2 
(b) the solution of an equation which is reducible to linear equation
(c) 2/x = 1 – y² + e^–y/2
(d) 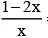= -y² + Ce^-y2/2

Correct Answer is option (a, b, d)

Given, dy/dx = xy + x²y³

Put,

Integrated Factor =

Q.2. The solution of 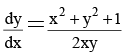satisfying y(1) = 1 is given by
(a) a system of hyperbola
(b) a system of circles
(c) y² = x(1 + x) – 1
(d) (x – 2)² + (y – 3)² = 5

Correct Answer is option (a, c)

Rewriting the given equation as
 
The I.F. of this equation is 1/x, so

⇒ y² = (x² - 1) + Cx. Since y(1) = 1 so C = 1,
Hence, y² = x(1 + x) -1 which represents a system of hyperbola.

Q.3. The differential equation of the curve for which intercept cut by any tangent on y-axis is equal to the length of the sub normal:
(a) is linear
(b) is homogeneous of first degree
(c) has separable variables
(d) is of first order

Correct Answer is option (a, b, d)

Let y = f(x) be the curve
Equation of tangent at (x, y) will be
Y – y = f '(x) (X – x)
Intercept cut by the tangent on y axis will be
y – x f '(x)
So y – xf '(x) =
This is homogeneous equation of first degree & first order Rewriting this equation = 1 which is a linear equation.

Q.4. The differential equation of the curve for which the initial ordinate of any tangent is equal to the corresponding subnormal –
(a) is linear
(b) is homogeneous of first degree
(c) has separable variables
(d) is second degree

Correct Answer is option (a, b)
y = f(x) is a curve
y – y = f ' (x) (X – x) is tangent at (x, y)
f ' (x) = dy/dx  X = 0

initial ordinate of tangent y – x f '(x).
The subnormal at this point is given by y dy/dx.
y dy/dx = y – x dy/dx

dy/dx = y/x + y

This is homogeneous equation

This is linear equation also.

Q.5. The solutions of y = x 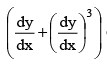are given by -
(a) The constant function y = 0
(b) y = 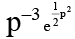(p + p³)
(c) y = 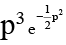(p + p³)
(d) = p^–2 + 1 

Correct Answer is option (a, b)
Clearly the constant function y = 0 is a solution. Differentiating the give equation w.r.t. x, we get
p = dy/dx  = (p + p³) + x
⇒ –p³ = x( 1 + 3p²) dp/dx

⇒ log xp³ = (1/2)p² + C ⇒ xp³ =
Putting value of x is in the given equation, we have
y = (p + p³)

Q.6. The solution of (dy/dx)² + 2y cot x dx/dy = y² is-
(a) y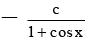= 0
(b) y = c/1 - cos x
(c) x = 2 sin^–1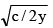 
(d) None of these 

Correct Answer is option (b, c)
Solving for dy/dx , we obtain

= y (–cot x ± cosec x)
Thus, we have y dy/y = (– cot x + cosec x) dx
⇒ log y =  – log sin x + log tan x/2 + log c
⇒
Solving dy/y = – (cot x + cosec x) dx, we get
y = 1/ 1 - cos x
⇒ x = 2 sin^–1

Q.7. The solution of y₁ (x²y³ + xy) = 1 is
(a) 1/x = 2 –y² +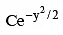
(b) the solution of an equation which is reducible to linear equation
(c) 2/x = 1 - y² + e^-y/2
(d)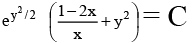

Correct Answer is option (a, b, d)

Re-writing the given equation, we have
dx/dy = x²y³ + xy
⇒ x^-2 dx/dy –x^–1 y = y³, which is reducible to linear form.
Putting x–1 = u. We have du/dy + yu = –y³
The I.F. of this equation is. So the solution is

Q.8. The solution of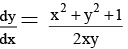satisfying y (1) = 1 is given by
(a) a system of hyperbola
(b) a system of circles
(c) y² = x (1 + x) –1
(d) (x –2)² + (y –3)² = 5

Correct Answer is option (a, c)
Re-writing, the given equation as
Putting y² = u, we have= 1/x + x.
The I.F. of this equation is 1/x, so u.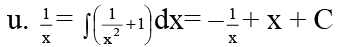
 
⇒ y² = (x² –1) + Cx.
Since, y(1) = 1 so C = 1,
Hence, y² = x (1 + x) –1 which represents a system of hyperbola.

Q.9. The solution of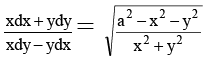is.
(a) 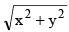= a (sin (tan^–1 y/x) + C
(b) = a ( cos (tan^–1 y/x) + C
(c) 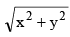= a (tan (sin–1 y/x) + const)
(d) y = x tan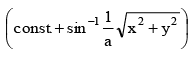

Correct Answer is option (a, d)
Taking, x = r cos θ and y = r sin θ so that x² + y² = r² and y/x = tan θ, we have  x dx + y dy = r dr and xdy - ydx = x² sec² θ d θ = r² d θ. The given equation can be transformed into

⇒ C + sin^–1 r/a = θ = tan^–1 y/x
⇒ y = x tan
or a sin (const + tan^–1 y/x)

Q.10. A normal is drawn at a point P(x, y) of a curve. It meets the x- axis at Q. If PQ is of constant length k. Such a curve passing through (0, k) is
(a) a circle with centre (0, 0)
(b) x² + y² = k²
(c) (1+ k)x² + y² = k²
(d) x² + (1 + k²) y² = k²

Correct Answer is option (a, b)
The equation of normal at P(x, y) is

Y – y = –
So, the coordinates of Q are
Thus PQ² = (X – x)² + (0 –y)² =

To find the equation of the curve we rewrite it as

Integrating, we get
...(3)
As the curve passes through (0, k), we get
= ± (0) + c ⇒ c = 0
Therefore, (3) can be written as

= ± x ⇒ ± k² – y² = x² or x² + y² = k²