GMAT Exam > GMAT Notes > Data Insights for GMAT > The Basic Principles of Data Sufficiency
The Basic Principles of Data Sufficiency | Data Insights for GMAT PDF Download
| Table of contents |

|
| Know How to Eliminate Data Sufficiency Answer Choices |

|
| The Statements are Always True |

|
| It’s All About the Question Stem |

|
| Think About Sufficiency, Not Calculation |

|
Know How to Eliminate Data Sufficiency Answer Choices
- As you’ve already learned, the directions and answer choices for Data Sufficiency questions never change, so it’s to your advantage to memorize them. But you can take this approach one step further by learning how to eliminate answer choices as you work through Data Sufficiency problems.

- As you evaluate the two statements, use your erasable notepad to keep track of which choices you have ruled out as incorrect. Use the following patterns to guide your elimination:

- Eliminating choices after evaluating each statement will allow you to attack the question more efficiently, without considering a choice you’ve already ruled out.
- You also want to avoid a common mistake on Data Sufficiency: choosing (C) when the answer is actually (A), (B), or (D).
Remember: if either statement by itself is sufficient, then of course the two statements together will also be sufficient since the statements are always true and never contradict each other. But (C) can be correct only when each statement alone is insufficient and combining the statements is necessary to obtain sufficiency. - You should consider the statements together only if each is insufficient on its own. When you evaluate the statements together, keep in mind that each statement is true. So if you’re picking numbers to evaluate the statements combined, you must choose values that are permitted by both statements.
The Statements are Always True
- The statements are new pieces of data that apply to the problem and are always true. Don’t waste time trying to verify a statement.
- The fact that the statements are always true has an important corollary that will help you catch careless errors: the statements will never contradict each other. Although they won’t always be sufficient to answer the question, they’ll never be mutually exclusive. If it appears that two statements are in disagreement with each other, you should recheck your work, because you have made an error.
Example: What is the value of t?
(1) t2 = t
(2) t + 6 = 6
~ This is a straightforward Value question for which you need a value of t.
~ Let’s say that you made an error in your analysis of Statement (1) and thought that t had to equal 1. You’d think that Statement (1) was sufficient.
~ Then you’d look at Statement (2). Simplifying, you’d learn that t equals 0.
~ That’s also sufficient. So you’d think that the answer would be (D).
~ However, according to your analysis, the statements contradict each other:
(1) t = 1
(2) t = 0
~ That isn’t possible. So you’d know to go back and recheck your work. Statement (2) pretty obviously says that t = 0, so you would recheck your work on Statement (1). Is 1 the only number that equals itself when squared? Substitute the 0 from Statement (2) and you get 02 = 0 × 0 = 0. So Statement (1) actually permits two values and is therefore insufficient.
(1) t = 0 or 1
(2) t = 0
The correct answer is (B), not (D).
It’s All About the Question Stem
- In Data Sufficiency questions, if you rush past the question and dive into the statements, you risk doing a whole bunch of unnecessary—and possibly misleading—math. You must understand the question stem before you analyze the statements. There’s a huge difference between a question that asks for a value (a Value question) and a question that asks for an answer of yes or no (a Yes/No question).
Consider this identical pair of statements:
(1) x3 = x
(2) x2 = x
(1) x3 = x
(2) x2 = x
Here’s how they evaluate:
(1) x = −1, 0, or 1
(2) x = 0 or 1
(1) x = −1, 0, or 1
(2) x = 0 or 1
But you still have no idea what the answers are without seeing the question stems:
What is the value of x? Is x < −1?
(1) x = −1, 0, or 1
(2) x = 0 or 1
(1) x = −1, 0, or 1
(2) x = 0 or 1 - For the question on the left, a Value question, Statement (1) is insufficient because there are three possible values of x. Statement (2) is also insufficient because it permits two possible values. Even when the statements are considered together, x could be either 0 or 1. That’s two values, which is insufficient for a Value question. The answer is (E).
- But the question on the right is a Yes/No question, so you will need to evaluate it differently. This question asks whether x is less than −1. First, look at Statement (1). Is −1 < −1? No. Is 0 < −1? No. Is 1 < −1? No. Always no: this statement is sufficient. The same for Statement (2): both values answer the question with a no, so it’s sufficient, as well. The answer is (D).
- That’s as different as two Data Sufficiency answers can be, and it had nothing to do with the statements, which were identical. It’s all about the question stem.
- But as you begin to attack a Data Sufficiency question, you want to look for more than just whether the question is a Value or a Yes/No question. You saw how Problem-Solving questions get much easier with some analysis and simplification before an approach is chosen. So too with Data Sufficiency.
Example: If w ≠ x, w ≠ z, and x ≠ y, is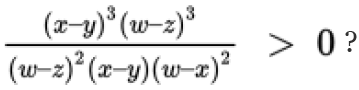
(1) x > y
(2) w > z
~ This is a Yes/No question that asks about a fraction containing multiple variable expressions as factors. At first glance, this may look like a scary question stem. But take a closer look at that fraction. There are a lot of shared terms in the numerator and the denominator. Using the laws of exponents, you can cancel the (w − z)2 and the (x − y) in the denominator:
If w ≠ x, w ≠ z, and x ≠ y, is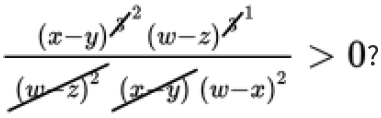
That simplifies the question to this:
If w ≠ x, w ≠ z, and x ≠ y, is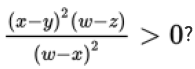
~ This is looking better already. You can simplify even further by thinking logically about the question. You aren’t asked for the value of anything, just whether this complicated fraction is positive. Without knowing anything about the values of w, x, y, and z, what can you already know about the answer to this question stem? Well, for one thing, you know that a squared term cannot be negative.
~ So there’s no way that (x − y)2 or (w − x)2 is negative. In fact, since w ≠ x and x ≠ y, they can’t be zero, either. So those two terms are both positive, which is the only thing that matters to the question. You can simplify the question even further, to this: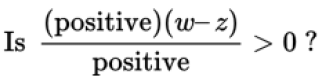
~ Since multiplying and/or dividing (w − z) by anything positive will not change its sign, you have this:
Is w − z > 0?
~ Now that’s a much simpler question. Look at how much easier the statements have become to evaluate:
(1) x > y
(2) w > z
Statement (1) is totally irrelevant to whether w − z > 0. This statement is insufficient.
Statement (2) tells you that w is bigger than z, so w − z must be positive. (Subtract z from both sides of the inequality, and you get w − z > 0.) That’s a definite yes. This is sufficient, so (B) is correct.
~ The more analysis and simplification you do with the question stem, the easier dealing with the statements will become.
Think About Sufficiency, Not Calculation
Get into the habit of thinking about what’s needed for sufficiency, rather than doing arithmetic calculations. One of the ways that the GMAT makes a Data Sufficiency question harder is to make the numbers scarier.
But if you aren’t worrying about arithmetic, you won’t be fazed by this. Let’s take a look at two important math concepts that can help you avoid number crunching in Data Sufficiency.
The N-Variables, N-Equations Rule
- Perhaps one of the most powerful tools to evaluate sufficiency is the N-variables, N-equations rule. If you have at least as many distinct, linear equations as you have variables, you will be able to solve for the unique numerical values of all the variables. If there are two variables, you need at least two equations to solve for all the values.
- If you have three variables, you need at least three equations. If you have four variables, you need at least four equations, and so on.
- Note that when you apply the n-variables, n-equations rule, you must be alert to the exact definition of the word distinct: each equation must provide new, different information. For instance, even though the equations x + 3y = 5 and 2x + 6y = 10 look different, they are not in fact distinct—the second equation is merely the first equation multiplied by 2.
- Another example is the following system of equations: x + 2y − 3z = 8, 2y + 6z = 2, and x + 4y + 3z = 10. These may also initially seem to be distinct, but a closer look reveals that the third equation is merely the sum of the first two. It therefore adds no new information, so this system of equations cannot be solved for unique numerical values for each variable.
Example: A souvenir shop made $2,400 in revenue selling postcards. If a large postcard costs twice as much as a small postcard, the shop sold 950 large postcards, and it sold no other type of postcard besides these two sizes, then how many small postcards did it sell?
(1) A large postcard costs $2. If the shop had sold 20 percent fewer small postcards, its revenue would have been reduced by 4 1/6 percent. - There are four factors that affect the outcome of this problem: (1) the price of a small postcard, (2) the price of a large postcard, (3) the number of small postcards sold, and (4) the number of large postcards sold.
- That’s four variables, so four distinct linear equations would enable you to solve for any of the variables. How many equations do you have already? Well, something-or-other equals $2,400 (that’s one), there’s a relationship between the prices (that’s two), and you get the number of large postcards (that’s three). With three equations for four variables, any new equation will be sufficient, as long as it is distinct and it doesn’t introduce a new variable.
- Statement (1) is a new equation and is therefore sufficient. Statement (2) is a more complicated equation, and it would likely be time-consuming to calculate. But it is still a new, distinct equation, and it is therefore sufficient. (D) is correct.
- Imagine how much time it would take to work through these equations. Using the n-variables, n-equations rule, it need take no longer than a minute. One word of caution, though: having the same number of distinct linear equations guarantees sufficiency, but having fewer does not guarantee insufficiency.
- The GMAT will set up equations so that you can sometimes solve for what’s asked even though you can’t solve for every variable individually.
Example: A fruit stand sells apples, pears, and oranges. If oranges cost $0.50 each, then what is the cost of 5 oranges, 4 apples, and 3 pears?
(1) The cost of 1 apple is $0.30.
(2) The cost of 8 apples and 6 pears is $3.90. - There are three variables in this problem (the cost of an orange, the cost of an apple, and the cost of a pear), so three distinct equations could solve for everything. You’re given only one (the exact price of an orange).
- So two additional distinct equations will guarantee sufficiency. But you should keep your eyes open for a way to answer your question with fewer. Since you already know the price of an orange, the only thing you’d need to answer your question is the price of 4 apples and 3 pears.
- Statement (1) is insufficient, as you still do not know anything about the price of a pear. Statement (2) is only one equation, but if you divided it by 2, you’d get the cost of 4 apples and 3 pears, which is exactly what you need. This statement is sufficient, so (B) is correct.
The document The Basic Principles of Data Sufficiency | Data Insights for GMAT is a part of the GMAT Course Data Insights for GMAT.
All you need of GMAT at this link: GMAT
|
24 videos|28 docs|21 tests
|
FAQs on The Basic Principles of Data Sufficiency - Data Insights for GMAT
| 1. What is data sufficiency on the GMAT exam? |  |
Ans. Data sufficiency is a unique question type found in the GMAT exam. In this type of question, you are given a problem followed by two statements labeled (1) and (2). Your task is to determine whether the information provided in these statements is sufficient to answer the problem, without relying on any additional data or calculations.
| 2. Are the statements always true in data sufficiency questions? |  |
Ans. No, the statements in data sufficiency questions may or may not be true. The key is to evaluate the sufficiency of the information provided in the statements, rather than focusing on their truthfulness. The statements can be true, false, or even provide contradictory information.
| 3. Why is it important to focus on the question stem in data sufficiency questions? |  |
Ans. The question stem provides the specific problem that needs to be answered. It is crucial to understand the requirements of the question stem before evaluating the sufficiency of the statements. By focusing on the question stem, you can determine the specific information needed to solve the problem and evaluate whether the given statements provide that information.
| 4. What should I consider when evaluating the sufficiency of the statements in data sufficiency questions? |  |
Ans. When evaluating the sufficiency of the statements, you should consider whether each statement alone is sufficient to answer the question, whether both statements together are sufficient, or whether additional information is needed. It is important to remember that you are not required to actually solve the problem or perform calculations. You only need to determine whether the given statements provide enough information to solve the problem.
| 5. How can I improve my performance in data sufficiency questions on the GMAT exam? |  |
Ans. To improve your performance in data sufficiency questions, practice is key. Familiarize yourself with the common question types and strategies for evaluating sufficiency. Learn to quickly identify the information needed from the question stem and effectively analyze the statements. Additionally, reviewing the basic principles and guidelines for data sufficiency questions can help you develop a systematic approach and avoid common pitfalls.
Related Searches















