Phase Difference & Phase Shift | Network Theory (Electric Circuits) - Electrical Engineering (EE) PDF Download

Phase Difference is used to describe the difference in degrees or radians when two or more alternating quantities reach their maximum or zero values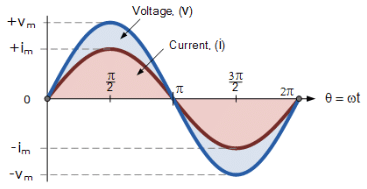

• Phasors are an effective way of analysing the behavour of elements within an AC circuit when the circuit frequencies are the same. The result of adding together two phasors depends on their relative phase, whether they are “in-phase” or “out-of-phase” due to some phase difference.
• A sinusoidal waveform is an alternating quantity that can be presented graphically in the time domain along a horizontal axis. As a time-varying quantity, sinusoidal waveforms have a positive maximum value at time π/2, a negative maximum value at time 3π/2, with zero values occurring along the baseline at 0, π and 2π points.
• However, not all sinusoidal waveforms will pass exactly through the zero axis point at the same time, but may be “shifted” to the right or to the left of 0o by some value when compared to another sine wave.
• For example, comparing a voltage waveform to that of a current waveform. This then produces an angular shift or Phase Difference between the two sinusoidal waveforms. Any sine wave that does not pass through zero at t = 0 has a phase shift.
• The difference or phase shift as it is also called of a Sinusoidal Waveform is the angle Φ (Greek letter Phi), in degrees or radians that the waveform has shifted from a certain reference point along the horizontal zero axis. In other words phase shift is the lateral difference between two or more waveforms along a common axis and sinusoidal waveforms of the same frequency can have a phase difference.
• The difference between phases, Φ of an alternating waveform can vary from between 0 to its maximum time period, T of the waveform during one complete cycle and this can be anywhere along the horizontal axis between, Φ = 0 to 2π (radians) or Φ  = 0 to 360^o depending upon the angular units used.
• Phase difference can also be expressed as a time shift of τ in seconds representing a fraction of the time period, T for example, +10mS or – 50uS but generally it is more common to express phase difference as an angular measurement.
• Then the equation for the instantaneous value of a sinusoidal voltage or current waveform we developed in the previous Sinusoidal Waveform will need to be modified to take account of the phase angle of the waveform and this new general expression becomes.

Phase Difference Equation

Where:
A_m – is the amplitude of the waveform.
ωt – is the angular frequency of the waveform in radian/sec.
Φ (phi) – is the phase angle in degrees or radians that the waveform has shifted either left or right from the reference point.

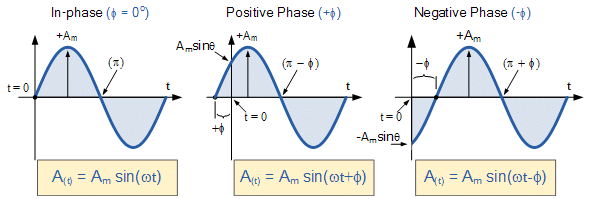
If the positive slope of the sinusoidal waveform passes through the horizontal axis “before” t = 0 then the waveform has shifted to the left so Φ >0, and the phase angle will be positive in nature, +Φ giving a leading phase angle. In other words it appears earlier in time than 0^o producing an anticlockwise rotation of the vector.

Likewise, if the positive slope of the sinusoidal waveform passes through the horizontal x-axis some time “after” t = 0 then the waveform has shifted to the right so Φ <0, and the phase angle will be negative in nature -Φ producing a lagging phase angle as it appears later in time than 0^o producing a clockwise rotation of the vector. Both cases are shown below.

Phase Relationship of a Sinusoidal Waveform

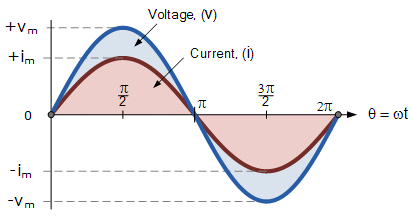
Firstly, lets consider that two alternating quantities such as a voltage, v and a current, i have the same frequency ƒ in Hertz. As the frequency of the two quantities is the same the angular velocity, ω must also be the same. So at any instant in time we can say that the phase of voltage, v will be the same as the phase of the current, i.

Then the angle of rotation within a particular time period will always be the same and the phase difference between the two quantities of v and i will therefore be zero and Φ = 0. As the frequency of the voltage, v and the current, i are the same they must both reach their maximum positive, negative and zero values during one complete cycle at the same time (although their amplitudes may be different). Then the two alternating quantities, v and i are said to be “in-phase”.

Two Sinusoidal Waveforms – “in-phase”

Now lets consider that the voltage, v and the current, i have a phase difference between themselves of  30^o, so (Φ  = 30^o or π/6 radians). As both alternating quantities rotate at the same speed, i.e. they have the same frequency, this phase difference will remain constant for all instants in time, then the phase difference of  30^o between the two quantities is represented by phi, Φ as shown below.

Phase Difference of a Sinusoidal Waveform

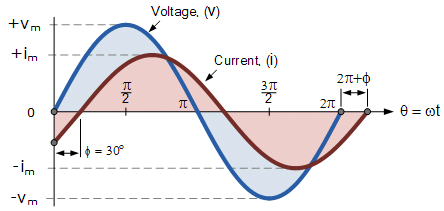
• The voltage waveform above starts at zero along the horizontal reference axis, but at that same instant of time the current waveform is still negative in value and does not cross this reference axis until 30^o later. Then there exists a difference in the phases between the two waveforms as the current cross the horizontal reference axis reaching its maximum peak and zero values after the voltage waveform.
• As the two waveforms are no longer “in-phase”, they must therefore be “out-of-phase” by an amount determined by phi, Φ and in our example this is 30^o. So we can say that the two waveforms are now 30^o out-of phase. The current waveform can also be said to be “lagging” behind the voltage waveform by the phase angle, Φ. Then in our example above the two waveforms have a Lagging Phase Difference so the expression for both the voltage and current above will be given as.
  Where current, i “lags” voltage, v by phase angle Φ
• Likewise, if the current, i has a positive value and crosses the reference axis reaching its maximum peak and zero values at some time before the voltage, v then the current waveform will be “leading” the voltage by some phase angle. Then the two waveforms are said to have a Leading Phase Difference and the expression for both the voltage and the current will be.
  
  Where current, i “leads” the voltage v by phase angle Φ
• The phase angle of a sine wave can be used to describe the relationship of one sine wave to another by using the terms “Leading” and “Lagging” to indicate the relationship between two sinusoidal waveforms of the same frequency, plotted onto the same reference axis. In our example above the two waveforms are out-of-phase by 30^o. So we can correctly say that i lags v or we can say that v leads i by 30^o depending upon which one we choose as our reference.
• The relationship between the two waveforms and the resulting phase angle can be measured anywhere along the horizontal zero axis through which each waveform passes with the “same slope” direction either positive or negative.
• In AC power circuits this ability to describe the relationship between a voltage and a current sine wave within the same circuit is very important and forms the bases of AC circuit analysis.

The Cosine Waveform

So we now know that if a waveform is “shifted” to the right or left of 0^o when compared to another sine wave the expression for this waveform becomes A_m sin(ωt ± Φ). But if the waveform crosses the horizontal zero axis with a positive going slope 90^o or π/2 radians before the reference waveform, the waveform is called a Cosine Waveform and the expression becomes.

Cosine Expression

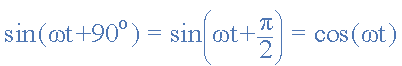
The Cosine Wave, simply called “cos”, is as important as the sine wave in electrical engineering. The cosine wave has the same shape as its sine wave counterpart that is it is a sinusoidal function, but is shifted by +90^o or one full quarter of a period ahead of it.

Difference between a Sine wave and a Cosine wave

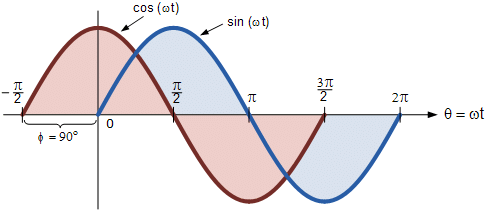
Alternatively, we can also say that a sine wave is a cosine wave that has been shifted in the other direction by -90^o. Either way when dealing with sine waves or cosine waves with an angle the following rules will always apply.

Sine and Cosine Wave Relationships

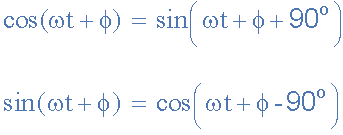
When comparing two sinusoidal waveforms it more common to express their relationship as either a sine or cosine with positive going amplitudes and this is achieved using the following mathematical identities.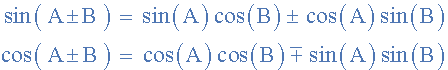

Therefore: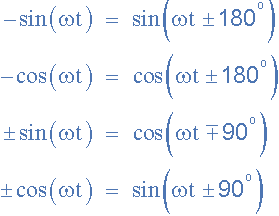

By using these relationships above we can convert any sinusoidal waveform with or without an angular or phase difference from either a sine wave into a cosine wave or vice versa.