Fast Decoupled Load Flow | Power Systems - Electrical Engineering (EE) PDF Download
The fast decoupled power flow method is a very fast and efficient method of obtaining power flow problem solution. In this method, both, the speeds as well as the sparsity are exploited. This is actually an extension of Newton-Raphson method formulated in polar coordinates with certain approximations which result into a fast algorithm for power flow solution.
This method exploits the property of the power system where in MW flow-voltage angle and MVAR flow-voltage magnitude are loosely coupled. In other words a small change in the magnitude of the bus voltage does not affect the real power flow at the bus and similarly a small change in phase angle of the bus voltage has hardly any effect on reactive power flow.
Because of this loose physical interaction between MW and MVAR flows in a power system, the MW- δ and MVAR-V calculations can be decoupled. This decoupling results in a very simple, fast and reliable algorithm. As we know, the sparsity feature of admittance matrix minimizes the computer memory requirements and results in faster computations. The accuracy is comparable to that of the N-R method.
The earlier equation of power flow studies [i.e. Eq. (6.119)] using N-R method can be written in polar coordinates as –
 ........(6.131)
........(6.131)
where H, N, M and L are the elements (viz., J1, J2, J3 and J4) of the Jacobian matrix.
Since changes in real power (i.e., ΔP) are less sensitive to the changes in voltage magnitude (i.e., ΔV) and changes in reactive power (i.e., ΔQ) are less sensitive to the changes in phase angle of voltage (i.e., Δδ), Eq. (6.131) can be reduced to – ........(6.132)
........(6.132)
The Eq. (6.132) is decoupled equation and can be expanded as – ........(6.133)
........(6.133) .......(6.134)
.......(6.134)
The next step in deriving the algorithm is to make suitable assumptions in deriving the expressions for H and L.
Off-diagonal element of H is –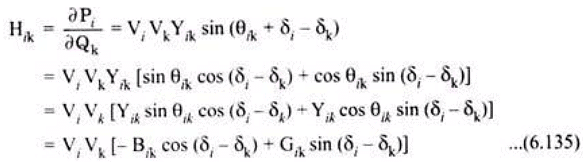
Similarly off-diagonal element of L is –
From Eqs. (6.135) and (6.136), we have –
The diagonal elements of H are given as –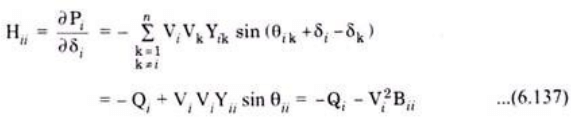
Similarly diagonal elements for the matrix are given as –
In the case of fast decoupled power flow method of power flow studies the following approximations are made for evaluating Jacobian elements.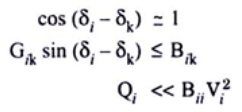 ........(6.139)
........(6.139)
With the above assumptions the Jacobian elements become – ........(6.140)
........(6.140)
With these Jacobian elements Eqs. (6.133) and (6.134) become – ........(6.141)
........(6.141) ........(6.142)
........(6.142)
Where Bik and Bik are elements of- Bik matrix.
Further decoupling and final algorithm for the fast-decoupled power-flow studies are obtained by:
(i) Omitting from B’, the representation of those network elements that affect MVAR flows, i.e., shunt reactances and off-nominal in phase transformer taps.
(ii) Omitting from B”, the angle shifting affects of phase shifters.
(iii) Dividing Eqs. (6.141) and (6.142) by Vi and assuming Vk = 1.0 pu and also neglecting series resistance in calculating the elements of B’.
With the above assumptions, Eqs. (6.141) and (6.142) for the power flow studies become: ........(6.143)
........(6.143) ........(6.144)
........(6.144)
In the above equations B’ and B” are real and sparse and have similar structures as those of H and L respectively. Since, they contain only network admittances, they are constant and do not change during successive iterations for solution of power flow problem, they need to be evaluated only once and inverted once during the first iteration and then used in all successive iterations.
It is due to the nature of Jacobian matrices B’ and B” and the sparsity of these matrices that the method is fast. In this method of power flow studies, each cycle of iteration consists of one solution for Δδ to update δ and one solution for ΔV to update V. The iterations are continued till ΔP and ΔQ at all load buses and Δ P at all generation buses are within prescribed (or assumed) tolerances.
|
21 videos|67 docs|45 tests
|

|
Explore Courses for Electrical Engineering (EE) exam
|

|
















