Measurement of Resistance | GATE Notes & Videos for Electrical Engineering - Electrical Engineering (EE) PDF Download
What is the Measurement of Resistance?
Resistance is one of the most basic elements encountered in electrical and electronics engineering. The value of resistance in engineering varies from very small value like, resistance of a transformer winding, to very high values like, insulation resistance of that same transformer winding. Although a multimeter works quite well if we need a rough value of resistance, but for accurate values and that too at very low and very high values we need specific methods. For this purpose we categories the resistance into three classes.
Measurement of Low Resistance (<1Ω)
The major problem in measurement of low resistance values is the contact resistance or lead resistance of the measuring instruments, though being small in value is comparable to the resistance being measured and hence causes serious error.Thus to eliminate this issue small valued resistance are constructed with four terminals. Two terminals are current terminals and other two are potential terminals.
Figure below shows the construction of low resistance.
 Low Resistance
Low Resistance
The current is flown through current terminals C1 and C2 while the potential drop is measured across potential terminals V1 and V2. Hence we can find out the value of resistance under experiment in terms of V and I as indicated in the above figure. This method helps us to exclude the contact resistance due to current terminals and though contact resistance of potential terminals still comes into picture, it is very small fraction of high resistance potential circuit and hence induces negligible error.
The methods employed for measurement of low resistances are:-
- Kelvin’s Double Bridge Method
- Potentiometer Method
- Ducter Ohmmeter.
Kelvin’s Double Bridge
Kelvin’s double bridge is a modification of simple Wheatstone bridge. Figure below shows the circuit diagram of Kelvin’s double bridge. Kelvin’s Double Bridge
Kelvin’s Double Bridge
As we can see in the above figure there are two sets of arms, one with resistances P and Q and other with resistances p and q. R is the unknown low resistance and S is a standard resistance. Here r represents the contact resistance between the unknown resistance and the standard resistance, whose effect we need to eliminate. For measurement we make the ratio P/Q equal to p/q and hence a balanced Wheatstone bridge is formed leading to null deflection in the galvanometer. Hence for a balanced bridge we can write

Putting eqn 2 in 1 and solving and using P/Q = p/q, we get-
 Hence we see that by using balanced double arms we can eliminate the contact resistance completely and hence error due to it. To eliminate another error caused due to thermo-electric emf, we take another reading with battery connection reversed and finally take average of the two readings. This bridge is useful for resistances in range of 0.1µΩ to 1.0 Ω.
Hence we see that by using balanced double arms we can eliminate the contact resistance completely and hence error due to it. To eliminate another error caused due to thermo-electric emf, we take another reading with battery connection reversed and finally take average of the two readings. This bridge is useful for resistances in range of 0.1µΩ to 1.0 Ω.
Ducter Ohmmeter
It is an electromechanical instrument used for measurement of low resistances. It comprises of a permanent magnet similar to that of a PMMC instrument and two coils in between the magnetic field created by the poles of the magnet. The two coils are at right angles to each other and are free to rotate about the common axis. Figure below shows a Ducter Ohmmeter and the connections required to measure an unknown resistance R.
One of the coil called current coil, is connected to current terminals C1 and C2, while the other coil called, voltage coil is connected to potential terminals V1 and V2. Voltage coil carries current proportional of the voltage drop across R and so is its torque produced. Current coil carries current proportional to the current flowing through R and so is its torque too. Both the torque acts in opposite direction and the indicator come to halt when the two are equal. This instrument is useful for resistance in range 100µΩ to 5Ω.
Measurement of Medium Resistance (1Ω – 100kΩ)
Following are the methods employed for measuring a resistance whose value is in the range 1Ω – 100kΩ –- Ammeter-Voltmeter Method
- Wheatstone Bridge Method
- Substitution Method
- Carey- Foster Bridge Method
- Ohmmeter Method
Ammeter Voltmeter Method
This is the most crude and simplest method of measuring resistance. It uses one ammeter to measure current, I and one voltmeter to measure voltage, V and we get the value of resistance as
Now we can have two possible connections of ammeter and voltmeter, shown in the figure below.
 Ammeter Voltmeter Method
Ammeter Voltmeter Method
Now in figure 1, the voltmeter measures voltage drop across ammeter and the unknown resistance, hence

Hence, the relative error will be,

For connection in figure 2, the ammeter measures the sum of current through voltmeter and resistance, hence

The relative error will be,

It can be observed that the relative error is zero for Ra = 0 in first case and Rv = ∞ in second case. Now the questions stand that which connection to be used in which case. To find out this we equate both the errors

Hence for resistances greater than that given by above equation we use the first method and for less than that we use second method.
Wheatstone Bridge Method
This is the simplest and the most basic bridge circuit used in measurement studies. It mainly consists of four arms of resistance P, Q; R and S. R is the unknown resistance under experiment, while S is a standard resistance. P and Q are known as the ratio arms. An EMF source is connected between points a and b while a galvanometer is connected between points c and d. Wheatstone Bridge
Wheatstone Bridge
A bridge circuit always works on the principle of null detection, i.e. we vary a parameter until the detector shows zero and then use a mathematical relation to determine the unknown in terms of varying parameter and other constants. Here also the standard resistance, S is varied in order to obtain null deflection in the galvanometer. This null deflection implies no current from point c to d, which implies that potential of point c and d is same. Hence

Combining the above two equations we get the famous equation –

Substitution Method
The figure below shows the circuit diagram for resistance measurement of an unknown resistance R. S is a standard variable resistance and r is a regulating resistance. Substitution Method
Substitution Method
First the switch is place at position 1 and the ammeter is made to read a certain amount of current by varying r. The value of ammeter reading is noted. Now the switch is moved to position 2 and S is varied in order to achieve the same ammeter reading as it read in the initial case. The value of S for which ammeter reads same as in position 1, is the value of unknown resistance R, provided the EMF source has constant value throughout the experiment.
Measurement of High Resistance (>100kΩ)
Following are few methods used for measurement of high resistance values-- Loss of Charge Method
- Megger
- Megohm bridge Method
- Direct Deflection Method
We normally utilize very small amount of current for such measurement, but still owing to high resistance chances of production of high voltages is not surprising. Due to this we encounter several other problems such as-
- Electrostatic charges can get accumulated on measuring instruments
- Leakage current becomes comparable to measuring current and can cause error
- Insulation resistance is one of the most common in this category; however a dielectric is always modeled as a resistor and capacitor in parallel. Hence while measuring the insulation resistance (I.R.) the current includes both the component and hence true value of resistance is not obtained. The capacitive component though falls exponentially but still takes very long time to decay. Hence different values of I.R. are obtained at different times.
- Protection of delicate instruments from high fields.
Hence to solve the problem of leakage currents or capacitive currents we use a guard circuit. The concept of guard circuit is to bypass the leakage current from the ammeter so as to measure the true resistive current. Figure below shows two connections on voltmeter and micro ammeter to measure R, one without guard circuit and one with guard circuit.
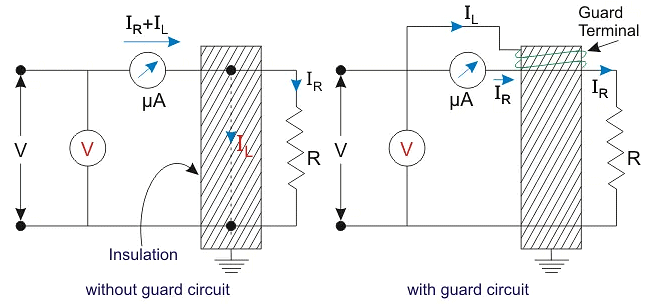
In the first circuit the micro ammeter measures both capacitive and the resistive current leading to error in value of R, while in the other circuit the micro ammeter reads only the resistive current.
Loss of Charge Method
In this method we utilize the equation of voltage across a discharging capacitor to find the value of unknown resistance R. Figure below shows the circuit diagram and the equations involved are- Loss of Charge Method
Loss of Charge Method

However the above case assumes no leakage resistance of the capacitor. Hence to account for it we use the circuit shown in the figure below. R1 is the leakage resistance of C and R is the unknown resistance.
We follow the same procedure but first with switch S1 closed and next with switch S1 open. For the first case we get

For second case with switch open we get

Using R1 from above equation in equation for R’ we can find R.
Megohm Bridge Method
In this method we use the famous Wheatstone bridge philosophy but in a slightly modified way. A high resistance is represented as in the figure below.
G is the guard terminal. Now we can also represent the resistor as shown in the adjoining figure, where RAG and RBG are the leakage resistances. The circuit for measurement is shown in the figure below.
 Megohm Bridge
Megohm Bridge
It can be observed that we actually obtain the resistance which is parallel combination of R and RAG. Although this causes very insignificant error.
Megger
Megger is one of the most important measuring device used by electrical engineers and is essentially used for measuring insulation resistance only. It consists of a generator which can be hand driven or nowadays we have electronic megger.
|
27 videos|328 docs
|
|
27 videos|328 docs
|

|
Explore Courses for Electrical Engineering (EE) exam
|

|

















