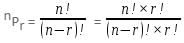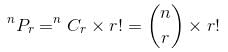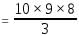This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Permutation & Combination (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:How many three-lettered passwords can be formed using the English alphabet, such that the three letters are different?
Explanation
There are 26 English alphabet and we need to find three-lettered passwords in which three letters are different, so
The number of passwords with different letters = 26 × 25 × 24
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:If three dice are rolled, find the number of possible outcomes in which at least one die shows 4.
Explanation
otal number of outcomes = 6 × 6 × 6 = 216 … (1)
Number of outcomes in which no die shows 4 = 5 × 5 × 5 = 125 … (2)
Number of outcomes in which at least 1 die shows 4 = (1) - (2)
= 216 - 125 = 91
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:There are 10 lamps in a hall. Each lamp can be switched on independently. The number of ways in which the hall can be illuminated is
Explanation
The hall can be illuminated by switching on at least one of the 10 lamps.
Therefore, the required number of ways is 210 - 1 = 1023.
Hence, option (2) is the correct answer.
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:A committee of five is to be chosen from among six men and four ladies. In how many ways can this be done in order to include at least one lady?
Explanation
Since we require at least 1 lady on the committee, we could have 1, 2, 3 or 4 ladies on the committee. A committee of 5 from among 10 people can be chosen in 10C5 ways = 252 ways. These ways include committees where there are no ladies. A committee with no ladies on it will have 5 men from among 6, i.e. 6C5 ways = 6 ways. So, the required number of ways = 252 - 6 = 246
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:A 5-character code is made from digits 0-9, such that they always exist in decreasing order in the code, e.g. 97530. How many such codes are possible?
Explanation
We just have to select 5 digits from the 10 available digits. When these five digits are selected, there is only one way in which these can exist in decreasing order.
Number of ways to select 5 digits out of 10 digits = 10C5
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:Which of the following is the relation between permutation and combination?
Explanation
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:How many 4-letter words can be formed using the letters of the word COLLEGE, if each letter has to be distinct?
Explanation
Distinct letters = C, O, L, E, G
Number of distinct 4-letter words = 5P4 = 5 × 4 × 3 × 2 = 120
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:The number of circular arrangements of 10 different things taken 3 at a time is
Explanation
Formula for number of circular arrangements of n different things taken r = nPr/r
Here, n = 10, r = 3
Total number of arrangements
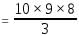
= 720/3
= 240
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:In a shopping mall, 7 elevators are installed exclusively for moving between the ground and first floors (4 moving upwards, 3 downwards) and 5 between the first and second floors (2 upwards, 3 downwards). Considering that Liza has to shop on every floor, in how many ways can she perform her journey to the top floor and back?
Explanation
Number of ways for going from ground floor to 1st floor = 4
Number of ways for going from 1st to 2nd floor = 2
Number of ways for going from 2nd to 1st floor = 3
Number of ways for going from 1st to ground floor = 3
∴ Total number of ways = 4 × 2 × 3 × 3
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 1
Try yourself:In how many ways can we select 6 men and 5 women from 10 men and 12 women?
Explanation
6 men can be chosen from 10 men in 10C6 ways.
5 women can be chosen from 12 women in 12C5 ways.
So, 6 men and 5 women can be chosen in 10C6 × 12C5 ways.
Report a problem