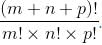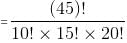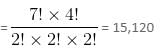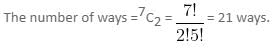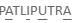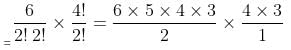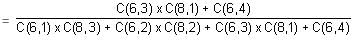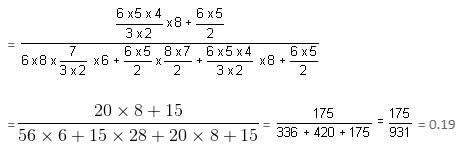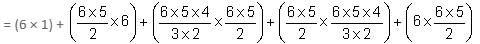This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Permutation & Combination (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Permutation & Combination - 1
Try yourself:In how many ways can 45 men be allotted to 3 different districts, if the districts are to be covered by 10, 15 and 20 men?
Explanation
The number of ways is the same as the number of ways in which m + n + p things can be divided into three groups containing m, n and p, which is 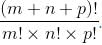
∴ The required number of different allotments 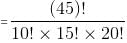
Report a problem
Question for Practice Questions Level 2: Permutation & Combination - 1
Try yourself:In the word 'MATHEMATICS', the positions of vowels and consonants are kept unchanged. How many different words can be formed by using different arrangements of the remaining letters?
Explanation
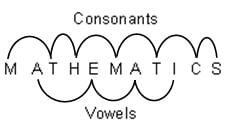
Different ways of arranging letters so that the positions of vowels and consonants remain unchanged
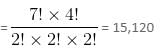
Report a problem
Question for Practice Questions Level 2: Permutation & Combination - 1
Try yourself:In how many ways can 8 identical balls be distributed in 3 distinct boxes so that none of the boxes remains empty?
Explanation
Suppose there are 3 boxes B1, B2, B3
In total there are 8 boxes we are going to put 1 ball in each box
So, the remaining number of balls after putting 1 ball in each box = 8 - 3 = 5
so number of remaining balls n = 5
the number of boxes r = 3
The number of ways for arranging the balls in boxes without any condition = (n + r - 1)Cr-1
n + r - 1 = 5 + 3 - 1 = 7
r - 1 = 3 - 1 = 2
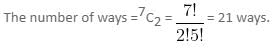
Report a problem
Question for Practice Questions Level 2: Permutation & Combination - 1
Try yourself:How many words can be formed with the letters of the word PATLIPUTRA without changing the relative positions of vowels and consonants?
Explanation
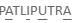
AIUA -- Vowels and 'PTLPTR' -- Consonants
Number of words that can be formed without changing the relative positions of vowels and consonants
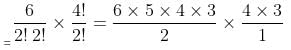
= 2160
Report a problem
Question for Practice Questions Level 2: Permutation & Combination - 1
Try yourself:In how many ways can two dice be rolled, so that the sum of the values on the upper faces is divisible by three?
Explanation
Out of the 36 possible outcomes, 12 outcomes will yield a score divisible by 3, i.e. a score of either 3, 6, 9 or 12.
The 12 outcomes will be various arrangements of (1, 2), (2, 1), (2, 4), (4, 2), (3, 3), (3, 6), (6, 3), (4, 5), (5, 4), (5, 1),(1, 5) and (6, 6).
Report a problem
Question for Practice Questions Level 2: Permutation & Combination - 1
Try yourself:A store carries four styles of pants. For each type, there are ten different possible waist sizes, six different pant lengths and four colour choices. How many different types of pants could the store have?
Explanation
Using the fundamental principle of multiplication, total number of types = 10 × 6 × 4 × 4 = 960
Report a problem
Question for Practice Questions Level 2: Permutation & Combination - 1
Try yourself:What is the number of words that can be formed by using the letters A, B, C, D, E and F, taken three at a time, if each word contains at least one vowel?
Explanation
Since we are taking three letters at a time, the total number of three letter words is 6P4 = 6 × 5 × 4 = 120. The number of words not containing A and E is 4P3 = 4 × 3 × 2 = 24. Therefore, the required number of words is 96.
Report a problem
Question for Practice Questions Level 2: Permutation & Combination - 1
Try yourself:In how many ways can 5 different coins be placed in small squares of a chess board (8 × 8), such that no two coins should be in the same row or column?
Explanation
The first coin can be placed in any box out of 64 boxes.
Second coin cannot be in the same row or column. So, there should be 64 - (8 + 7) = 49 squares left, and so on.
Required number of ways = 64 × 49 × 36 × 25 × 16 = (6720)2
Report a problem
Question for Practice Questions Level 2: Permutation & Combination - 1
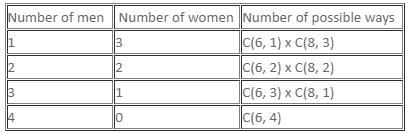
Try yourself:A group consists of 6 men and 8 women. A committee of 4 has to be formed with at least one man. The probability that the committee so formed has a greater number of men than women is
Explanation
Report a problem
Question for Practice Questions Level 2: Permutation & Combination - 1
Try yourself:8 men and 6 women are working in an office. 9 of them are to be chosen for a meeting that should include at least 3 men and 2 women. 2 men present in the last meeting must attend this meeting as well. The number of ways in which they can be selected is
Explanation
There are 8 men and 6 women. Two men are fixed, so we have 6 men and 6 women for selection. Now, out of 9 persons, 2 men are fixed, so we have to select the rest 7 persons, including at least 1 man and 2 women.
Possible cases are as follows.
(1) 1 man, 6 women = C(6, 1) × C(6, 6)
(2) 2 men, 5 women = C(6, 2) × C(6, 5)
(3) 3 men, 4 women = C(6, 3) × C(6, 4)
(4) 4 men, 3 women = C(6, 4) × C(6, 3)
(5) 5 men, 2 women = C(6, 5) × C(6, 2)
So, total number of ways = [C(6, 1) × C(6, 6) + C(6, 2) × C(6, 5) + C(6, 3) × C(6, 4) + C(6, 4) × C(6, 3) + C(6, 5) × C(6, 2)]
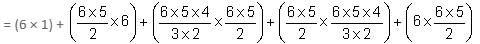
= 6 + 90 + 300 + 300 + 90 = 786
Report a problem