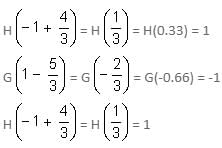This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Functions (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Functions
Try yourself:If f : A → B is defined such that f(x) = 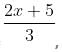 then f -1(x) = ?
then f -1(x) = ?
Explanation
f(x) = 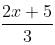
Let f(x) be y.
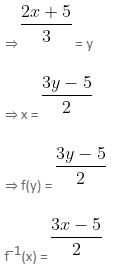
Report a problem
Question for Practice Questions Level 3: Functions
Try yourself:If f(x) = xa + ax and g(x) = xa - ax , then find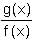 , when x = 2 and a = 3.
, when x = 2 and a = 3.
Explanation
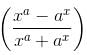
For x = 2 and a = 3
We have,
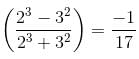
Report a problem
Question for Practice Questions Level 3: Functions
Try yourself:When f(x) - f(-x) = 0, the function f(x) is called an even function. Which of the following functions is an even function?
Explanation
Report a problem
Question for Practice Questions Level 3: Functions
Try yourself:A function satisfies f(0, n) = n + 1 and f(m + 1, n) = f(m, f(m, n)). What is the value of f(4, 100)?
Explanation
f(4, 100) = f[3, f(3, 100)] …………(1)
f(3, 100) = f[2, f(2, 100)] ……….. (2)
f(2, 100) = f[1, f(1, 100)] …………(3)
f(1, 100) = f[0, f(0, 100)] ……….. (4)
f(0, 100) = 100 + 1 = 101.
f(1, 100) = f(0, 101) = 102
f(2, 100) = f(1, 102) …………. (5)
f(1, 102) = f[0, f(0, 102)] = f(0, 103) = 104
Put in (5) = f(2, 100) = 104
Put this value in (2),
f(3, 100) = f(2, 104) …………… (6)
Now, f(2, 104) = f[1, f(1, 104)] …………… (7)
f(1, 104) = f[0, f(0, 104)] = f(0, 105) = 106
Put in (7)... and so on
f(4, 100) = 116
Report a problem
Question for Practice Questions Level 3: Functions
Try yourself:If f(x) satisfies 2f(x) + f(1 – x) = x2 for all x, then f(x) is equal to
Explanation
The given equation 2f(x) + f(1 – x) = x2 holds for all x.
2f(x) + f(1 – x) = x2.......(i)
In particular, the equation holds, if we replace x with 1 – x.
Thus, we deduce that 2f(1 – x) + f(x) = (1 – x)2.
2f(1 – x) + f(x) = (1 – x)2..............(ii)
Multiply equation (i) by 2 and then subtract equation (ii) from equation (i).
Thus, we get:
3f(x) = 2x2 – (1 – x)2 = x2 + 2x – 1
f(x) = (x2 + 2x – 1)/3
Report a problem
Question for Practice Questions Level 3: Functions
Try yourself:Let f(x) be a polynomial with integer coefficients, for which 3 and 13 are the roots. Which of the following could possibly be the value of f(10)?
Explanation
The given information implies that f(x) = (x – 3) (x – 13) g(x), where g(x) is a polynomial with integer coefficients. Hence, f(10) = – 21g(10), so that 21 must be a divisor of f(10). The only choice divisible by 21 is 42, so the correct answer is 42. To check if f(x) exists, consider f(x) = – 2(x – 3) (x – 13).
Report a problem
Question for Practice Questions Level 3: Functions
Try yourself:A function f(x) is called even if f(-x) = f(x) for all x and it is called odd if f(-x) = -f(x) for all x. Which of the following statements is/are true?
(i) The product of an even function and an odd function is even.
(ii) The sum of two even functions is even.
(iii) The product of two odd functions is even.
Explanation
Statement (i): Let F(x) be an even function and G(x) be odd.
H(x) = Product of an even function and an odd function
H(x) = F(x) G(x)
Now, H(-x) = F(-x) G(-x) = F(x) (-G(x)) = -F(x) G(x) = -H(x)
Hence, H(x) is an odd function. Statement (i) is not true.
Statement (ii): Let F(x) and G(x) be even functions.
H(x) = F(x) + G(x)
H(-x) = F(-x) + G(-x) = F(x) + G(x) = H(x)
It is an even function; hence, statement (ii) is true.
Statement (iii): Let F(x) and G(x) be odd functions.
H(x) = F(x) G(x)
H(-x) = F(-x) G(-x) = (-F(x))(-G(x)) = F(x) G(x) = H(x)
It is an even function. Hence, statement (iii) is true.
So, statements (ii) and (iii) are true.
Report a problem
Question for Practice Questions Level 3: Functions
Try yourself:For all real numbers x, a function f(x) satisfies 2f(x) + f(1 - x) = x2. Find the value of f(5).
Explanation
Given: 2f(x) + f(1 - x) = x2 ... (A)
Put x = 5 in (i).
2f(5) + f(-4) = 25
Multiply by 2
4f(5) + 2f(-4) = 50 ... (1)
Put x = -4 in (A).
2f(-4) + f(5) = 16 ... (2)Subtract (2) from (1):
4f(5) - f(5) = 50 - 16
3f(5) = 34
f(5) = 34/3
Report a problem
Question for Practice Questions Level 3: Functions
Try yourself:Which of the following is the graph of f(x) = 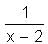 ?
?
Explanation
f(x) = 1/(x - 2)
When x = 1, f(x) = -1
When x = 2, f(x) = ∞
When x = 3, f(x) = 1, and so on
Therefore, option d is correct.
Report a problem
Question for Practice Questions Level 3: Functions
Try yourself:Refer to the following data to answer the question that follows.
F(x) = Modulus of x
G(x) = The largest integer less than or equal to x
H(x) = The smallest integer greater than or equal to x
I(x) = x, a real number
Find the value of H
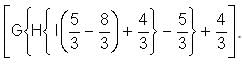
Explanation
I 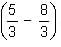 = I (-1) = -1
= I (-1) = -1
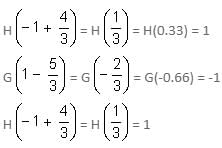
Report a problem
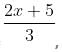 then f -1(x) = ?
then f -1(x) = ?
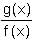 , when x = 2 and a = 3.
, when x = 2 and a = 3.
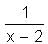 ?
?
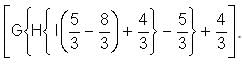

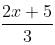
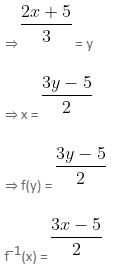
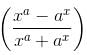
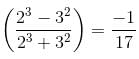
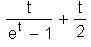 … (1)
… (1)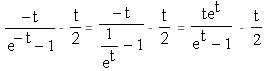
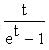 (1 - et) + t = -t + t = 0
(1 - et) + t = -t + t = 0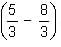 = I (-1) = -1
= I (-1) = -1