This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Inequalities (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:N is a negative real number. Which of the following is not true?
Explanation
The absolute value of any number N is always non-negative.
|N| = N, when N > 0 and |N| = -N, when N < 0.
Since N is a negative number, therefore |N| = N is not true.
Report a problem
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:The number of solutions of the equation |x2 - 4| = 4 + x2 is
Explanation
|x2 - 4| = 4 + x2
Case I: If x2 - 4 ≥ 0
i.e. x ≤ -2 and x ≥ 2
Then, |x2 - 4| = x2 - 4
⇒ The given equation becomes x2 - 4 = 4 + x2.
⇒ -4 = 4; which is not possible.
Case II: If x2 - 4 < 0
⇒ -2 < x < 2
Then, |x2 - 4| = - (x2 - 4)
Thus, the given equation becomes - (x2 - 4) = 4 + x2.
Or 2x2 = 0
⇒ x = 0
Hence, the given equation has only one solution.
Report a problem
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:Which of the following is not true at all?
Explanation
Take x = 2, then option (1), (2) will become true and hence those are not the answers.
Take x = – 2, option (4) will be true and hence not the answer.
But for any value of x, 2x > x.
So option (3) is not true at all. It is always false.
Report a problem
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:A, B, C and D are four friends and they are having w, x, y and z amount, respectively, such that w - z > 0, x - z < 0 and y - z < 0. Which of the following is necessarily true?
Explanation
w - z > 0
x - z < 0; this means z - x > 0
y - z < 0; this means z - y > 0
The product of cubes of three positive numbers will also be positive.
Report a problem
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:If a < b, then the solution of x2 - (a + b) x + ab < 0 is
Explanation
x2 - (a + b) x + ab < 0
(x - a) (x - b) < 0
a < x < b
Report a problem
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:What values of 'm' satisfy the inequality 3m2 - 21m + 30 < 0?
Explanation
3m2 - 21m + 30 < 0
m2 - 7m + 10 < 0
⇒ (m - 5)(m - 2) < 0
⇒ 2 < m < 5
Report a problem
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:What is the best description of 'x' which satisfies the inequality x2 - 5x + 6 ≤ 0 ?
Explanation
x2 - 5x + 6 ≤ 0
⇒ (x - 3)(x - 2) ≤ 0
⇒ x ∈ [2, 3] or 2 ≤ x ≤ 3
Therefore, option 4 is the correct answer.
Report a problem
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:x – |x| is always
Explanation
|x| is always positive.
If x is positive, x – |x| = 0.
If x is negative, x – |x| < 0.
Report a problem
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:Solve the system of inequalities:
5x + 2 > 3x - 1
3x + 1 > 7x - 4
Explanation
(i) 5x + 2 > 3x - 1 or 2x > -3
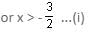
(ii) 3x + 1 > 7x - 4
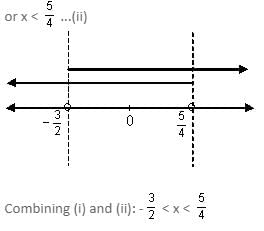
Report a problem
Question for Practice Questions Level 1: Inequalities - 1
Try yourself:3x2 – 7x + 4 ≤ 0
Explanation
At x = 0, inequality is not satisfied. Thus, option (c) is rejected. Also x = 0 is not a solution of the equation. Since, this is a continuous function, the solution cannot start from 0. Thus options (a) and (b) are not right. Further, we see that the given function is quadratic with real roots. Hence, option (d) is also rejected.
Report a problem