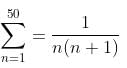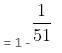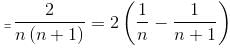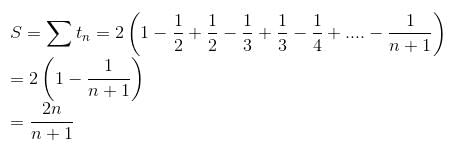This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Progressions, Sequences & Series (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself:The interior angles of a polygon are in A.P. If the least angle is 42° and common difference is 33°, the number of sides is
View Solution
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself:If the sum of the series 1 + 3/x +9/x2 + 27/x3 + … to infinity exists, then which of the following must be true?
(Given that x is not less than or equal to zero)
(Given that x is not less than or equal to zero)
View Solution
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself:If x, y, z are in A.P, then (x + 2y - z)(2y + z - x)(z + x - y) equals
View Solution
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself:In a GP, the third term is 10 more than the second term and the second term is 6 more than the first term. What is the fifth term?
View Solution
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself:If the sum of the first 8 terms of an AP is exactly half of the sum of the next 8 terms, what is the ratio of the 16th term to the 8th term of the AP?
View Solution
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself:Sweety purchased a box of chocolates. She ate 1 chocolate on the first day, 3 on the second day, 6 on the third day, 10 on the fourth day and so on. Finally, she finished all the chocolates in exactly 20 days. How many chocolates were there in the box?
View Solution
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself:The sums of odd and even numbered terms of an infinite GP are in the ratio of 3 : 2. What is the common ratio (r)?
View Solution
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself:If log3 2, log3 (2x - 5) and log3 (2x - 7/2) are in arithmetic progression, then the value of x is equal to
View Solution
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself: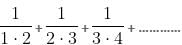 up to 50 terms is equal to
up to 50 terms is equal to
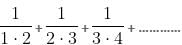 up to 50 terms is equal to
up to 50 terms is equal to
View Solution
Question for Practice Questions Level 2: Progressions, Sequences & Series - 1
Try yourself: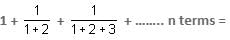
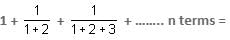
View Solution
Download as PDF
Related Searches

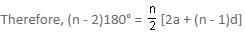
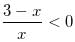
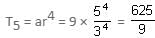
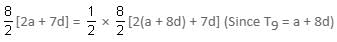
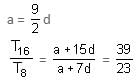
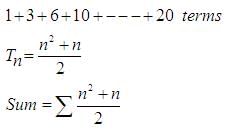
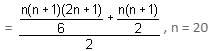
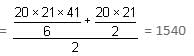
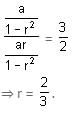
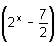 are in AP, therefore we can write:
are in AP, therefore we can write: