Understanding Quadrilaterals Class 8 Notes Maths Chapter 3
| Table of contents |

|
| Introduction |

|
| Sum of the Measures of the Exterior Angles of a Polygon |

|
| Kinds of Quadrilaterals |

|
| Some Special Parallelograms |

|
Introduction
Imagine you’re building a giant puzzle, and each piece has four sides. Some pieces are tall and narrow, others are wide and flat, but they all share one thing in common—they each have four sides. These special puzzle pieces are called quadrilaterals.
Quadrilaterals are like the four-sided heroes of geometry, with each one having its own unique personality. Some have all sides equal, some have just a pair of sides that are parallel, and others might look a little lopsided but are still important in their own way.
What is Plane Surface?
A plane surface is a flat surface that extends in all directions without curving or bending. It is characterized by the property that any two points on the surface can be connected by a straight line that lies entirely on the surface.
Imagine a sheet of paper. It is perfectly flat, which means if you place a ruler or any straight object on it, it will touch the surface at every point along its length without leaving any gaps. Plane surfaces that are two-dimensional, meaning they have length and width, but no thickness.
What is Plane Curve ?
A curve is a flat shape created by connecting multiple points without lifting the pencil from the surface.
Types of Curves
- Open Curve: A curve that does not start and end at the same point.
 Open Plane Curve
Open Plane Curve
- Closed Curve: A curve that starts and ends at the same point.
 Closed Plane Curve
Closed Plane Curve
- Simple Closed Curve: A closed curve is a simple closed curve, if it does not pass through a point more than once.
 Simple Closed Curve
Simple Closed Curve
What is a Polygon?
A polygon is a simple closed curve made up of line segments only. Polygons are classified according to the number of sides they have.
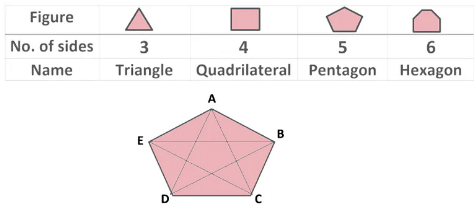
Some Important Terms
- Adjacent Sides: If the two sides of a polygon have a common vertex (or corner) then they are called the adjacent sides of the polygon. In the given figure above, AE and AB are adjacent sides of the Polygon ABCDE as they have the common vertex A.
- Adjacent Vertices: The two endpoints of the same side of the polygon are called adjacent vertices. In the given figure, A and E are adjacent vertices as they are the two endpoints of the side AE.
- Diagonals: The line segment joining two non-adjacent vertices are called diagonals of the polygon. In the figure, AD, AC, EB, EC, and BD are the diagonals of the polygon ABCDE.
Concave and Convex Polygon
1. Concave Polygons
A polygon is a concave polygon if a line segment joining two different points does not lie completely inside the polygon.

2. Convex Polygons
A polygon is a convex polygon if the line segment joining any two points lies completely inside the polygon.
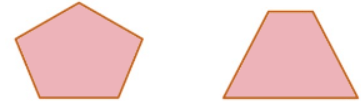
Regular and Irregular Polygons
1. Regular Polygons:
A polygon whose all sides and all angles are equal is called a Regular Polygon. A square has sides of equal length and angles of equal measure, i.e., 90° Regular Polygons
Regular Polygons
Equiangular means 'equal angles', and equilateral means 'equal sides'. Regular polygons have both of these properties.
Similarly, an Equilateral Triangle has sides of equal length and angle of equal measure i.e., 60°.
Therefore, a square and an equilateral triangle are Regular Polygons.
2. Irregular Polygons:
Polygons which do not have all the sides and angles of equal measure is called an Irregular Polygon. For examples a right angled triangle and a rectangle. Irregular Polygons
Irregular Polygons
Note: A rectangle is equiangular, i.e., it has equal angles, but it is does not have equal sides. Therefore, it is an irregular polygon.
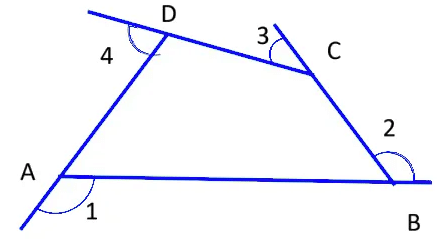
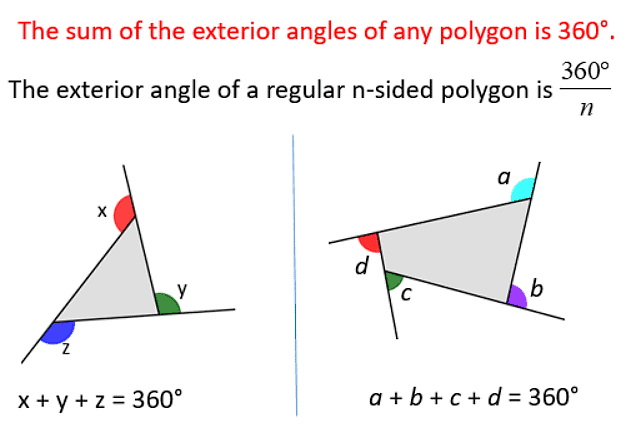
Sum of the Measures of the Exterior Angles of a Polygon
Let, the exterior angles of the quadrilateral ABCD be ∠1, ∠2, ∠3 and ∠4.
∠1 and ∠DAB forms a linear pair and the sum of the angles of a linear pair is 180°
∠1+∠DAB=180° (1)
Similarly, we can find out the sum of all linear pairs in the polygon:
∠2+∠CBA =180° (2)
∠3 + ∠DCB = 180° (3)
∠4 +∠ADC = 180° (4)
Adding the equations (1), (2), (3) and (4)
∠1+∠DAB + ∠2+∠CBA+∠3 + ∠DCB +∠4 +∠ADC =
180° + 180° +180° +180°Grouping the interior and exterior angles together:
(∠1+∠2+∠3+∠4) + (∠DAB+∠CBA+∠DCB+∠ADC)
(∠1+∠2+∠3+∠4) + 360° = 720°
(Sum of the interior angles of the quadrilateral is equal to 360°)
∠1+∠2+∠3+∠4 = 720° – 360°
∠1+∠2+∠3+∠4 = 360°
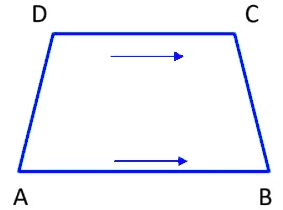
Kinds of Quadrilaterals
1. Trapezium
Trapezium is a quadrilateral with a pair of opposite parallel sides, while the other pair of sides are not parallel.
- ABCD is a trapezium, where AB ‖CD
- AD and BC are its non-parallel sides.
2. Kite
Kite is a special type of quadrilateral in which the two pairs of adjacent sides are equal.
- The opposite sides are unequal.
- Diagonals of a kite intersect each other at right angles.
ABCD is a kite, where AB = AD and BC = CD.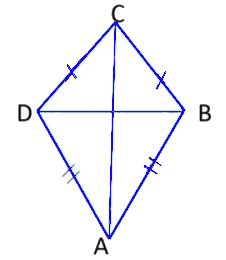
3. Parallelograms
A parallelogram is a quadrilateral whose opposite sides are parallel.
Properties of Parallelograms
(a) The opposite sides of a parallelogram are of equal length.
(b) The opposite angles of a parallelogram are of equal measure.
(c) The adjacent angles in a parallelogram are supplementary.
(d) The diagonals of a parallelogram bisect each other.
Each diagonal divides parallelogram into a set of congruent triangles.
Congruent triangles, as you know, are triangles that are exactly the same in size and shape. They have the exact same sides and the same angles, even though they might be rotated or flipped.
Let us prove the above property
In the parallelogram ABCD,
AB = CD and BC = AD
(Opposite sides are equal)
∠A =∠C and ∠B =∠D (Opposite angles are equal)
AO = OC and BO = OD (Diagonals bisect each other)
ΔABC ≅ ΔCDA and ΔBCD ≅ ΔDAB (Each diagonal divides a parallelogram into two congruent triangles)
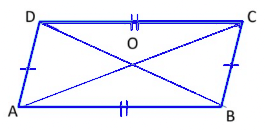 A Parallelogram
A Parallelogram
Some Special Parallelograms
1. Rhombus
- It is a parallelogram with all sides of equal length.
- Opposite angles are equal.
- Diagonals are perpendicular to each other.
- Diagonals bisect each other at right angles.
In Rhombus ABCD,
AB = BC = CD = DA (All the sides of a rhombus are equal)
∠A =∠C and ∠B =∠D (Opposite angles are equal)
AO = OC and BO = OD (Diagonals bisect each other)
∠AOB = ∠BOC = 90° (Diagonals bisect each other at right angles)
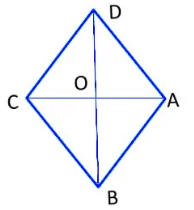 Rhombus
Rhombus
2. A Rectangle
- A rectangle is a parallelogram whose each angle is a right angle.
- The diagonals of a rectangle are equal and bisect each other, but not at right angles.
In rectangle ABCD,
∠A = ∠B = ∠C = ∠D = 90°
(Each angle of a rectangle is a right angle)
AC = BD (Diagonals of a rectangle are equal)
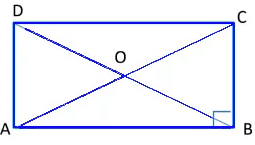
3. A Square
- A square is similar to a rectangle but it has equal sides.
- The diagonals are of equal length.
- The diagonals bisect each other perpendicularly.
In square ABCD,
∠A = ∠B = ∠C =∠D = 90°
(Each angle of a square is a right angle)
AC = BD (Diagonals of a rectangle are equal)
∠AOB = ∠BOC = 90° (Diagonals bisect each other at right angles)
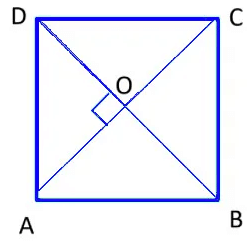
|
81 videos|423 docs|31 tests
|
FAQs on Understanding Quadrilaterals Class 8 Notes Maths Chapter 3
| 1. What is the sum of the measures of the exterior angles of a polygon? |  |
| 2. How do you classify different types of quadrilaterals? |  |
| 3. What are the properties of a parallelogram? |  |
| 4. What distinguishes a rectangle from a square? |  |
| 5. Can you explain the characteristics of a rhombus? |  |