JEE Main Previous year questions (2021-22): Properties of Triangle | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. Let PQRS be a quadrilateral in a plane, where QR = 1, ∠ PQR = ∠QRS = 70∘, ∠PQS = 15∘ and ∠PRS = 40∘. If ∠RPS = θ∘, PQ = α and PS = β, then the interval(s) that contain(s) the value of 4αβsinθ∘ is/are (JEE Advanced 2022)
(a) (0, √2)
(b) (1, 2)
(c) (√2, 3)
(d) (2√2, 3√2)
Ans. a and b
Applying sine rule in △PQR,
Applying sine rule in △PRS,
⇒ β sinθ = sin 40°
From (i) and (ii),
Using cos 0∘ = 1, cos 30∘ = (√3/2), cos 45∘ = 1√2 and cos 60∘ = 12
Only Options (A) and (B) are correct.
Q.2. The angle of elevation of the top of a tower from a point A due north of it is α and from a point B at a distance of 9 units due west of A is cos−1(3/√13). If the distance of the point B from the tower is 15 units, then cotα is equal to : (JEE Main 2022)
(a) 6/5
(b) 9/5
(c) 4/3
(d) 7/3
Ans. a
h = 10 units
Q.3. A horizontal park is in the shape of a triangle OAB with AB = 16. A vertical lamp post OP is erected at the point O such that ∠PAO = ∠PBO = 15° and ∠PCO = 45°, where C is the midpoint of AB. Then (OP)2 is equal to (JEE Main 2022)
(a) 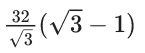
(b) 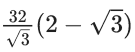
(c) 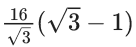
(d) 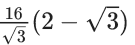
Ans. b
OP = OAtan15 = OBtan15 ...... (i)
OP = OCtan45 ⇒ OP = OC ...... (ii)
OA = OB ....... (iii)
OC2 + 82 = OA2
OP2 + 64 = OP2((√3+1)/(√3−1))2
Q.4. The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d,α) is : (JEE Main 2022)
(a) (10(√3 - 1), 25)
(b) (10(√3 - 1), (25/2))
(c) (10(√3 + 1), 25)
(d) (10(√3 + 1), (25/2))
Ans. a
Let BR = x
2x = 10(√3 − 1)
x = 5(√3 − 1)
d = 2x = 10(√3 − 1)
α = (1/2)(x + 10)(10 − x√3) = Area (PQRB)
Q.5. Let a vertical tower AB of height 2h stands on a horizontal ground. Let from a point P on the ground a man can see upto height h of the tower with an angle of elevation 2α. When from P, he moves a distance d in the direction of 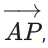 he can see the top B of the tower with an angle of elevation α. If
he can see the top B of the tower with an angle of elevation α. If 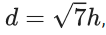 then tanα is equal to (JEE Main 2022)
then tanα is equal to (JEE Main 2022)
(a) (√5) - 2
(b) (√3) - 1
(c) (√7) - 2
(d) (√7) - (√3)
Ans. c
ΔAPM gives
tan 2α = (h/x) ..... (i)
ΔAQB gives
From (i) and (ii)
Let t = tan α
⇒ t2 - 2√7 t + 3 = 0
t = (√7) - 2
Q.6. A tower PQ stands on a horizontal ground with base Q on the ground. The point R divides the tower in two parts such that QR =15 m. If from a point A on the ground the angle of elevation of R is 60° and the part PR of the tower subtends an angle of 15° at A, then the height of the tower is : (JEE Main 2022)
(a) 5(2√3 + 3)m
(b) 5(√3 + 3)m
(c) 10(√3 + 1)m
(d) 10(2√3 + 1)m
Ans. a
For ΔAQR,
tan60° = (15/x) ....... (1)
From ΔAQP,
tan 75° = (h/x)
Q.7. The lengths of the sides of a triangle are 10 + x2, 10 + x2 and 20 − 2x2. If for x = k, the area of the triangle is maximum, then 3k2 is equal to : (JEE Main 2022)
(a) 5
(b) 8
(c) 10
(d) 12
Ans. c
⇒ 10−x2 = 2x2
3x2 = 10
x = k
3k2 = 10
Q.8. Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let (π/8) and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then tan2θ is equal to (JEE Main 2022)
(a) 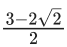
(b) 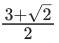
(c) 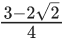
(d) 
Ans. c
From (i) and (ii)
Q.9. From the base of a pole of height 20 meter, the angle of elevation of the top of a tower is 60°. The pole subtends an angle 30° at the top of the tower. Then the height of the tower is : (JEE Main 2022)
(a) 15√3
(b) 20√3
(c) 20 + 10(√3)
(d) 30
Ans. d
Here AB is a tower and CD is a pole.
In triangle ABC,
In triangle BED,
tan30° = (h/x) ...... (2)
Divide equation (1) by equation (2), we get
⇒ 3h = 20 + h
⇒ h = 10m
∴ Height of tower = 20 + 10 = 30m
Q.10. Consider a triangle PQR having sides of lengths p, q and r opposite to the angles P, Q and R, respectively. Then which of the following statements is (are) TRUE? (JEE Advanced 2021)
(a) 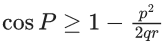
(b) 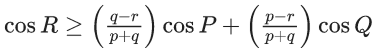
(c) 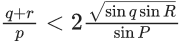
(d) If p < q and p < r, then cos Q > (p/r) and cos R > (p/q)
Ans. a and b
For option (a)
⇒ q2 + r2 ≥ 2qr
From Eq. (i), we get
⇒ cos P ≥ 1 − (p2/2qr) → option (a) is correct.
For option (b)
⇒ 4λ2 − 2λ = 0
⇒ u.v = 0 (Rejected)
or u.v = (1/2)
∴ u.v = (1/2)
∴ |3u+5v|2 = 9|u|2 + 25|v|2 + 3 × 5 × 2 × u.v
= 9 + 25 + 30 × (1/2)
= 49 (∵ |u| = |v| = 1, given)
∴ |3u + 5v| = 7
Hence, option (b) is correct.
For option (c)
→ option (c) is incorrect.
For option (d)
If p < q and p < r, then p is the smallest side and hence one of Q or R can be obtuse.
So, one of cos Q and cos R can be negative.
Therefore, cos Q > (p/r) and cos R >(p/q) cannot hold always.
Option (d) is incorrect.
Q.11. In a triangle ABC, let AB = √23, BC = 3 and CA = 4. Then the value of 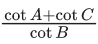
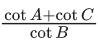 is _________. (JEE Advanced 2021)
is _________. (JEE Advanced 2021)
Ans. 2
Given,
AB = √23 = c
BC = 3 = a
CA = 4 = b
Now,
Q.12. A vertical pole fixed to the horizontal ground is divided in the ratio 3 : 7 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a point on the ground 18 m away from the base of the pole, then the height of the pole (in meters) is : (JEE Main 2021)
(a) 12√15
(b) 12√10
(c) 8√10
(d) 6√10
Ans. b
Let height of pole = 10l
use tanα = l/6 ⇒ l =
height of pole =
Q.13. Two poles, AB of length a metres and CD of length a + b (b ≠ a) metres are erected at the same horizontal level with bases at B and D. If BD = x and tan∠ACB = (1/2), then: (JEE Main 2021)
(a) x2 + 2(a + 2b)x − b(a + b) = 0
(b) x2 + 2(a + 2b)x + a(a + b) = 0
(c) x2 − 2ax + b(a + b) = 0
(d) x2 − 2ax + a(a + b) = 0
Ans. c
tanθ = 1/2
⇒ x2 − 2ax + ab + b2 = 0
Q.14. Let 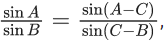 where A, B, C are angles of triangle ABC. If the lengths of the sides opposite these angles are a, b, c respectively, then : (JEE Main 2021)
where A, B, C are angles of triangle ABC. If the lengths of the sides opposite these angles are a, b, c respectively, then : (JEE Main 2021)
(a) b2 − a2 = a2 + c2
(b) b2, c2, a2 are in A.P.
(c) c2, a2, b2 are in A.P.
(d) a2, b2, c2 are in A.P.
Ans. b
As A, B, C are angles of triangle.
A + B + C = π
A = π − (B + C) ...... (1)
Similarly sinB = sin(A + C) ..... (2)
From (1) and (2)
sin(C+B).sin(C−B) = sin(A−C)sin(A+C)
sin2C − sin2B = sin2A − sin2C
∵ {sin(x + y)sin(x − y) = sin2x − sin2y}
2sin2C = sin2A + sin2B
By sine rule
2c2 = a2 + b2
⇒ b2, c2 and a2 are in A.P.
Q.15. A 10 inches long pencil AB with mid point C and a small eraser P are placed on the horizontal top of a table such that PC = √5 inches and ∠PCB = tan-1(2). The acute angle through which the pencil must be rotated about C so that the perpendicular distance between eraser and pencil becomes exactly 1 inch is : (JEE Main 2021)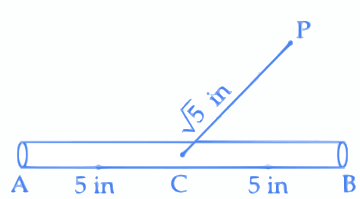
(a) tan-1 (3/4)
(b) tan-1 (1)
(c) tan-1 (4/3)
(d) tan-1 (1/2)
Ans. a
From figure,
sin β = 1/√5
∴ tanβ = 1/2tan(α+β) = 2
tan α = (3/4)
α = tan-1(3/4)
Q.16. A spherical gas balloon of radius 16 meter subtends an angle 60° at the eye of the observer A while the angle of elevation of its center from the eye of A is 75°. Then the height (in meter) of the top most point of the balloon from the level of the observer's eye is : (JEE Main 2021)
(a) 8(2 + 2√3 + 2)
(b) 8(√6 + √2 + 2)
(c) 8(√2 + 2 + √3)
(d) 8(√6 − √2 + 2)
Ans. b
→ centre of sphere
P, Q → point of contact of tangents from A
Let T be top most point of balloon & R be foot of perpendicular from O to ground.
From triangle OAP, OA = 16cosec30° = 32
From triangle ABO, OR = OA sin75° =So level of top most point = OR + OT
= 8(√6 + √2 + 2)
Q.17. Let in a right angled triangle, the smallest angle be θ. If a triangle formed by taking the reciprocal of its sides is also a right angled triangle, then sinθ is equal to : (JEE Main 2021)
(a) 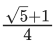
(b) 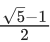
(c) 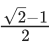
(d) 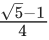
Ans. b
Let a ΔABC having C = 90° and A = θ
Also for triangle of reciprocals
⇒ 1 + sec2θ = cosec2θ
⇒ 1 − cos22θ = 4cos2θ
cos22θ + 4cos2θ − 1 = 0
cos2θ = −2 ± √5
cos2θ = √5 − 2 = 1 − 2sin2θ
⇒ 2sin2θ = 3 − √5
Q.18. If in a triangle ABC, AB = 5 units, ∠B = cos−1(3/5) and radius of circumcircle of ΔABC is 5 units, then the area (in sq. units) of ΔABC is : (JEE Main 2021)
(a) 10 + 6√2
(b) 8 + 2√2
(c) 6 + 8√3
(d) 4 + 2√3
Ans. c
As, cosB = (3/5) ⇒ B = 53°
As, R = 5 ⇒ (c/sinc) = 2R
⇒ (5/10) = sinc ⇒ C = 30°
Now, (b/sinB) = 2R ⇒ b =2(5)(4/5)= 8
Now, by cosine formula
⇒ a2 − 6a − 3g = 0
⇒ 3 + 4√3 (Reject a = 3 − 4√3)
Now,
⇒ Δ = (6 + 8√3)
⇒ Option (3) is correct.
Q.19. A pole stands vertically inside a triangular park ABC. Let the angle of elevation of the top of the pole from each corner of the park be (π/3). If the radius of the circumcircle of ΔABC is 2, then the height of the pole is equal to : (JEE Main 2021)
(a) (1/√3)
(b) 2√3
(c) √3
(d) (2√3)/3
Ans. b
Let PD = h, R = 2
As angle of elevation of top of pole from A, B, C are equal. So D must be circumcentre of ΔABC
tan(π/3) = PD/R = h/R
h = R tan(π/3) = 2√3
Q.20. The triangle of maximum area that can be inscribed in a given circle of radius 'r' is : (JEE Main 2021)
(a) An equilateral triangle having each of its side of length √3r.
(b) An equilateral triangle of height 2r/3.
(c) A right angle triangle having two of its sides of length 2r and r.
(d) An isosceles triangle with base equal to 2r.
Ans. a
Area of triangle ABC
A = (1/2) x (BC) x (AM)
(dA/dx) = 0 ⇒ x = (r/2)
Sign change of (dA/dx) at x = r/2
⇒ A has maximum at x = r/2
⇒ AB = AC = √3r
Q.21. A man is observing, from the top of a tower, a boat speeding towards the lower from a certain point A, with uniform speed. At that point, angle of depression of the boat with the man's eye is 30° (Ignore man's height). After sailing for 20 seconds, towards the base of the tower (which is at the level of water), the boat has reached a point B, where the angle of depression is 45°. Then the time taken (in seconds) by the boat from B to reach the base of the tower is : (JEE Main 2021)
(a) 10(√3 + 1)
(b) 10(√3 - 1)
(c) 10
(d) 10√3
Ans. a
x + y = √3h ...... (1)
Also,
h/y = tan 45°
h = y ..... (2)
put in (1)
x + y = √3y
x = (√3−1)y
(x/20) = ′v′ speed
∴ time taken to reach Foot from B = y/V
= 10(√3 + 1)
Q.22. The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 20 seconds at the speed of 432 km/hour, the angle of elevation changes to 30°. If the jet plane is flying at a constant height, then its height is : (JEE Main 2021)
(a) 3600√3 m
(b) 1200√3 m
(c) 1800√3 m
(d) 2400√3 m
Ans. b
v = 432×(1000/(60×60))) m/sec = 120 m/sec
Distance AB = v × 20 = 2400 meter
In ΔPAC
In ΔPBD
tan30° = (h/PD) ⇒PC = √3h
PD = PC + CD
h = 1200√3 meter
Q.23. Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is : (JEE Main 2021)
(a) 30
(b) 25
(c) 20√3
(d) 25√3
Ans. d
∴ tan(90 − θ) = (x/75)
and tanθ = (3x/75)
As cotθ.tanθ = 1
∴ (x/75).(3x/75) = 1
⇒ x = 25√3
Q.24. If a rectangle is inscribed in an equilateral triangle of side length 2√2 as shown in the figure, then the square of the largest area of such a rectangle is _____. (JEE Main 2021)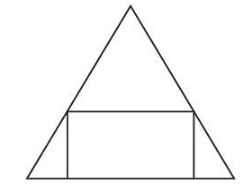
Ans. 3
In ΔDBF
A = Area of rectangle = l × b
l = √2
⇒ A2 = 3
Q.25. In ΔABC, the lengths of sides AC and AB are 12 cm and 5 cm, respectively. If the area of ΔABC is 30 cm2 and R and r are respectively the radii of circumcircle and incircle of ΔABC, then the value of 2R + r (in cm) is equal to _____. (JEE Main 2021)
Ans. 15
Area = (1/2)(5)(12)sinθ = 30
sinθ = 1 ⇒ θ = (π/2)
Δ is right angle Δ
r = (s − a) tan (A/2)
r = (s − a) tan (90/2)
r = (s − a)
2R + r = s, (As a = 2R)
Q.26. Let ABCD be a square of side of unit length. Let a circle C1 centered at A with unit radius is drawn. Another circle C2 which touches C1 and the lines AD and AB are tangent to it, is also drawn. Let a tangent line from the point C to the circle C2 meet the side AB at E. If the length of EB is α + √3 β, where α, β are integers, then α + β is equal to _____. (JEE Main 2021)
Ans. 1
(i) √2r + r = 1
r = 1/((√2) + 1)
r = (√2) − 1
(ii) CC2 = 2(√2) − 2 = 2(√2−1)
From ΔCC2N = sin∅ =
ϕ = 30°
(iii) In ΔACE apply sine law
∴ EB = 1 − (√3 − 1)
= 2 − √3
∴ α = 2, β = −1 ⇒ α + β = 1
|
347 docs|185 tests
|
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|







































































































































