Polynomials Class 9 Notes Maths Chapter 2
| Table of contents |

|
| Introduction |

|
| Polynomials in One Variable |

|
| Zeroes of a Polynomial |

|
| Factorization of Polynomials |

|
| Algebraic Identities |

|
| Summary |

|
Introduction
Welcome to the intriguing world of polynomials! These mathematical expressions, made up of numbers and variables, are essential in algebra and help us model real-life situations.
In this chapter, we'll explore what polynomials are, their different types, and their significance. You'll learn how to add, subtract, and multiply them, as well as how to factor them.
Get ready to discover the power of polynomials and how they can enhance your understanding of mathematics!
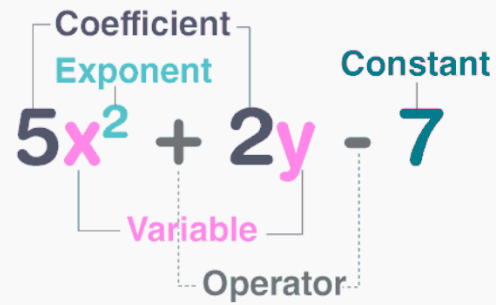
A polynomial is made up of one or more terms. Each term typically includes:
- A coefficient (a numerical value),
- A variable (like x, y, etc.),
- And an exponent (a power of the variable).
For example, in the polynomial:
4x3 - 3x2 + 2x -5
- The terms are 4x3 3x2 + 2x -5
Variable is denoted by a symbol that can take any real value, often represented by letters such as x, y, z, etc
Coefficient: the coefficient is simply the number that multiplies the variable in any given term of a polynomial. Each term of the polynomial has a coefficient.
Algebraic expressions are the mathematical equations consisting of variables, constants, terms and coefficients.
Expressions like 2x, 3x, -x, and -½ x are examples of algebraic expressions. Specifically in the form (a constant) x. When the constant is unknown, it is denoted as a, b, c, etc.
Polynomial
A polynomial is an algebraic expression consisting of variables, coefficients, and exponents, combined using addition, subtraction, and multiplication operations.
- Example:2x3−5x 2+ 3x −7 is a polynomial.
“The expression which contains one or more terms with non – zero coefficient is called polynomial”
Understanding Expressions with Examples
- Consider a square of side 3 units, where the perimeter is given by the sum of the lengths of its four sides.
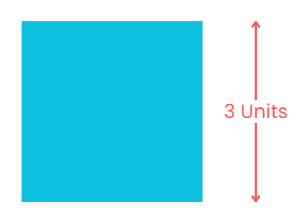
- If each side is x units, the perimeter is expressed as 4x units, showcasing how the value of the variable influences the result.
- The area of the square, denoted as x² square units, is an example of an algebraic expression.
Polynomials in One Variable
Polynomials are algebraic expressions with variables, coefficients, and exponents. When the exponents are whole numbers, the expressions are termed polynomials in one variable.
Example: x³ - x² + 4x + 7 and 3y² + 5y.
Terms and Coefficients
In a polynomial like x² + 2x, x² and 2x are referred to as terms. Each term has a coefficient—in -x³ + 4x² + 7x - 2, coefficients are -1, 4, 7, and -2. The term x⁰ (where x⁰ = 1) is also present.
Constant Polynomials and Zero Polynomials
Constants like 2, -5, and 7 are examples of constant polynomials. The constant polynomial 0 is termed the zero polynomial, a significant concept in polynomial theory.
Non-Polynomial Expressions
Expressions like x + 2/x, x⁻¹, and x + 3√(x) aren't polynomials due to non-whole number exponents.
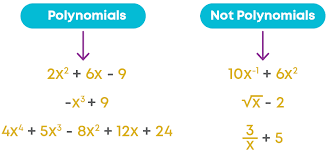
Notation for Polynomials
Polynomials can be denoted by symbols like p(x), q(x), or r(x), where the variable is x. Examples include:
- p(x) = 2x 2+ 5x−3
- q(x) = x 3−1
- r(y) = y 3+ y + 1
- s(u) = 2−u −u 2+ 6u 5
Degree of a Polynomial
The degree of a polynomial is the highest power of its variable. For example, in 3x⁷ - 4x⁶ + x + 9, the degree is 7. Constant polynomials have a degree of 0.
Examples:
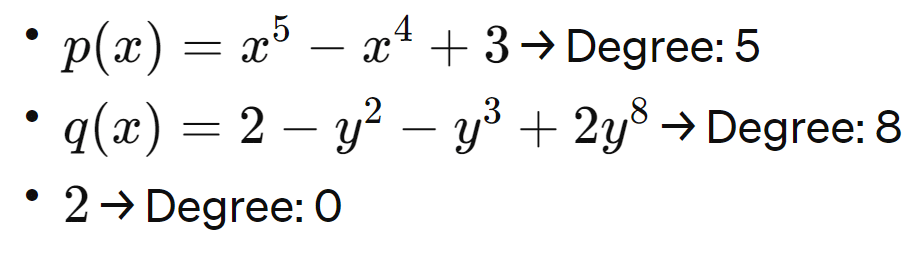
Linear, Quadratic, and Cubic Polynomials
Linear Polynomial: Degree 1, written as ax+b where a is not equal to 0.
Examples: 2x−1, 2y+1, 2−u
Quadratic Polynomial: Degree 2, expressed as ax2+bx+c where a is not equal to 0.
Examples: 5−y2, 4y+5y2, 6−y−y2
Cubic Polynomial: Degree 3, in the form ax3+bx2+cx+d where a is not equal to zero 0.
Examples: 4x3, 2x3+1, 5x3+x2
General Form of a Polynomial
A polynomial in one variable x of degree n is an expression of the form
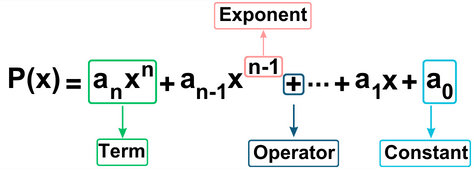
Zero Polynomial and Beyond
The zero polynomial, denoted as 0, has an undefined degree. Polynomials can extend to more than one variable,
like x2+y2+xyz in three variables.
Zeroes of a Polynomial
Consider the polynomial p(x)=5x3 − 2x2 + 3x −2. To find the value of p(x) at different points, we substitute the given values for x.
For Example, Given Polynomial: p(x) = 5x3 - 2x2 + 3x - 2
Calculation:
1. For x = 1:
p(1) = 5 - 2 + 3 - 2 = 4
2. For x = 0:
p(0) = 0 - 0 + 0 - 2 = -2
3. For x = -1:
p(-1) = -5 - 2 - 3 - 2 = -12
In summary, for the given polynomial p(x)=5x3−2x2+3x−2:
- p(1)=4
- p(0)=−2
- p(−1)=−12
These values are found by substituting the respective values of x into the polynomial expression.
Example: Value of Polynomials at Given Points
(i) For p(x)=5x2−3x+7 at x=1: p(1)=5(1)2−3(1)+7=9
(ii) For q(y)=3y3−4y+11 at y=2: q(2)=3(2)3−4(2)+11=27−8+11=30
(iii) For p(t)=4t4+5t3−t2+6 at t=a: p(a)=4a4+5a3−a2+6
Identifying Zeros of Polynomials
When evaluating p(x)=x−1 at x=1, we find that p(1)=0. In general, if p(c)=0, we say that c is a zero of the polynomial p(x). For example, for p(x)=x−1, x=1 is a zero.
Zero Polynomial and Constant Polynomials
Constant polynomials like 5 have no zeros since replacing x by any number in 5x0 still gives 5. The zero polynomial, denoted by 0, has every real number as its zero by convention.
Factorization of Polynomials
Factor Theorem
If p(x) is a polynomial of degree n>1 and a is any real number, then (i) x−a is a factor of p(x) if p(a)=0, and (ii) p(a)=0 if x−a is a factor of p(x).
Proof: By the Remainder Theorem, p(x)=(x−a)q(x)+p(a).
(i) If p(a)=0, then p(x)=(x−a)q(x), showing that x−a is a factor.
(ii) Since x−a is a factor of p(x), p(x)=(x−a)g(x) for some polynomial g(x). In this case, p(a)=(a−a)g(a)=0.
Example: Examining Factors
Examine whether x+2 is a factor of x3+3x2+5x+6 and of 2x+4. Let p(x)=x3+3x2+5x+6 and s(x)=2x+4.
Solution: For p(−2): p(−2)=(−2)3+3(−2)2+5(−2)+6=0, so x+2 is a factor.
For s(−2): s(−2)=2(−2)+4=0, so x+2 is a factor.
In fact, 2x+4=2(x+2), confirming the result without the Factor Theorem
Algebraic Identities
Algebraic identities are equations that hold true for all values of the variables involved. You may be familiar with several identities from earlier classes:
Identity I: (x+y)2=x2+2xy+y2
Identity II: (x−y)2=x2−2xy+y2
Identity III: x2−y2=(x+y)(x−y)
Identity IV: (x+a)(x+b)=x2+(a+b)x+ab
Example: Product Computation using Identities Problem
Find the following products using appropriate identities:
(i) (x+2)(x+2)
(ii)(x−4)(x+6)
Solution:
(i) For (x+2)(x+2), apply Identity I: (x+2)(x+2)=(x+2)2=x2+2(x)(2)+22=x2+4x+4
(ii) For (x−4)(x+6), use Identity IV: (x−4)(x+6)=x2+(−4+6)x+(−4)(6)=x2+2x−24
Identity V : (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2zx
Identity VI:
The identity (x+y)3=x3+y3+3xy(x+y) represents the cube of a binomial.
Similarly, by replacing y with −y, we get
Identity VII: (x−y)3=x3−y3−3xy(x−y).
Example: Expanded Forms of Cubes
(i) For (2a+3b)3:
(ii) For (3x−2y)3:
Identity VIII:
The identity x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx) expresses a factorization involving the sum and product of cubes.
Example: Factorization of 8x3+y3+27z3−18xyz
Given the expression 8x3+y3+27z3−18xyz, we can factorize it using Identity VIII:
8x3+y3+27z3−18xyz=(2x+y+3z)(4x2+y2+9z2−2xy−3yz−6xz)
Summary
1. Definition of a Polynomial:
A polynomial p(x) in one variable x is an algebraic expression written as, , where are constants and
, where are constants and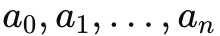 and an
and an
The term an is the leading coefficient and n is the degree of the polynomial.
2. Types of Polynomials:
- Monomial: A polynomial with one term.
- Binomial: A polynomial with two terms.
- Trinomial: A polynomial with three terms.
- Linear Polynomial: A polynomial of degree one.
- Quadratic Polynomial: A polynomial of degree two.
- Cubic Polynomial: A polynomial of degree three.
3. Zeros of Polynomials:
A real number a is a zero of a polynomial p(x) if p(a) = 0. Such a number is also called a root of the equation p(x) = 0.
4. Uniqueness and Existence of Zeros:
- Every linear polynomial has a unique zero.
- A non-zero constant polynomial has no zeros.
- Every real number is a zero of the zero polynomial (polynomial where all coefficients are zero).
5. Factor Theorem:
x - a is a factor of the polynomial p(x) if p(a) = 0. Conversely, if x - a is a factor of p(x), then p(a) = 0.
6. Algebraic Identities:
- For 2 variables (x and y) :

- For 3 variables (x, y and z)
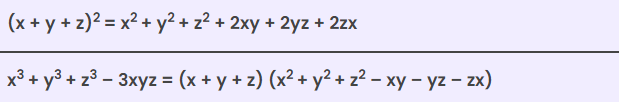
|
40 videos|471 docs|57 tests
|
FAQs on Polynomials Class 9 Notes Maths Chapter 2
| 1. What is a polynomial in one variable? |  |
| 2. How do you find the zeroes of a polynomial? |  |
| 3. What is the factorization of polynomials? |  |
| 4. What are some commonly used algebraic identities related to polynomials? |  |
| 5. Why is understanding polynomials important in mathematics? |  |
















