Introduction to Euclid’s Geometry Class 9 Notes Maths Chapter 5
| Table of contents |

|
| Introduction |

|
| Euclid’s Definitions, Axioms and Postulates |

|
| Some Euclid’s axioms |

|
| Euclid’s Five Postulates |

|
| Summary |

|
Introduction
The word ‘geometry’ comes from the Greek word ‘geo’, meaning the ‘earth’, and ‘metron’, meaning ‘to measure’. Thus, the word ‘geometry’ means ‘earth measurement’.- Geometry seems to have started from the need to measure land and was explored in various ways by ancient civilisations, including Egypt.
- The Egyptians created several geometric methods and rules to calculate simple areas and to perform basic constructions. They used geometry to calculate the volumes of granaries and for building canals and pyramids.

- Excavations in the Indian subcontinent, such as in Harappa and Mohenjo-Daro, show that the Indus Valley Civilization (around 3000 BC) made extensive use of geometry. This society was highly organised, with well-planned cities featuring parallel roads and an underground drainage system.
- Thales, a Greek mathematician, is known for providing the first proof that a circle is bisected by its diameter.
- Around 300 BC, Euclid, a mathematics teacher in Alexandria, Egypt, compiled all existing knowledge into his well-known work, called ‘Elements’. He organised it into thirteen chapters, referred to as books.
Euclid’s Definitions, Axioms and Postulates
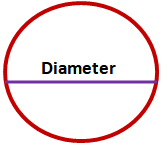
In Euclid’s era, mathematicians developed the concepts of a point, line, and plane from observing the space and solids around them. This led to a more abstract understanding of solid objects.
A solid has a shape, size, and position, and can be moved about. Therefore, a solid has three dimensions.
- Its edges are called surfaces.
- These surfaces separate different parts of space and are considered to have no thickness.
- The edges of the surfaces consist of curves or straight lines, which end in points.

Some of the other assumptions or definitions listed by Euclid’s are:
(i) A point is that which has no part.
(ii) A line is a breadthless length.
(iii) The ends of a line are points.
(iv) A straight line is a line which lies evenly with the points on itself.
(v) A surface is that which has length and breadth only.
(vi) The edges of a surface are lines.
(vii) A plane surface is a surface which lies evenly with the straight lines on itself.
Now, let's look at the first definition of a point. Here, we need to explain what a 'part' is. If we say that a 'part' occupies 'area', then we must also explain what 'area' means. This leads to a never-ending series of definitions. For this reason, mathematicians decide to leave some geometric terms undefined. However, we have a basic understanding of what a point is, even if the definition doesn't fully capture it. We often represent a point as a dot, even though a dot has some size.
Similarly, the second definition of a line talks about length and width, which are also not defined. Because of this, some terms remain undefined as a study progresses. In geometry, we consider a point, a line, and a plane (which Euclid calls a plane surface) as undefined terms. The important thing is that we can represent them in a straightforward way or describe them using 'physical models'.
Starting from his definitions, Euclid made certain assumptions that were not meant to be proven. These assumptions are called 'obvious universal truths'. He categorised them into two types: axioms and postulates. Common notions, often known as axioms, are used throughout mathematics and are not specifically related to geometry. For these reasons, mathematicians agree to leave some geometric terms undefined.
He divided them into two types:


Some Euclid’s axioms
(1) Things which are equal to the same thing are equal.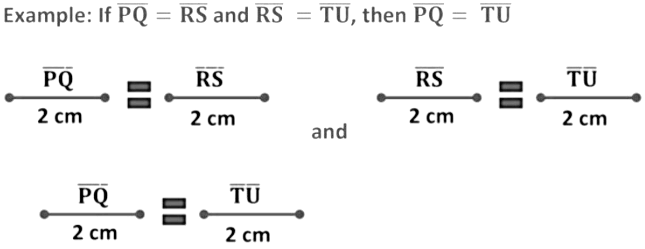 So,
So,
If line segment PQ is equal to line segment RS and line segment RS is equal to line segment TU, then line segment PQ is equal to line segment TU.
(2) If equals are added to equals, the wholes are equal.
Two jars, A and B have the same quantity of sugar, which is 2 kg.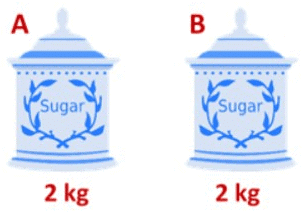
Now, we add 1 kg of sugar to both the jars, A and B.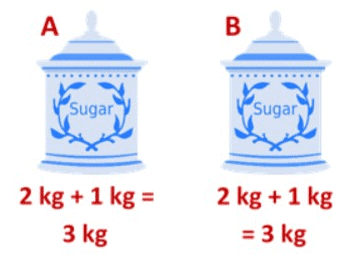 We see that the final quantity of sugar is the same in both the jars.
We see that the final quantity of sugar is the same in both the jars.
(3) If equals are subtracted from equals, the remainders are equal.
We again take the example of two jars having the same quantity of sugar (2 kg).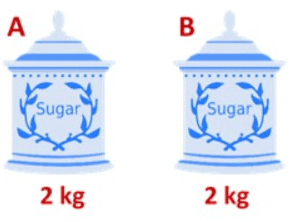 In this case, we remove 1 kg of sugar from both the jars, A and B.
In this case, we remove 1 kg of sugar from both the jars, A and B.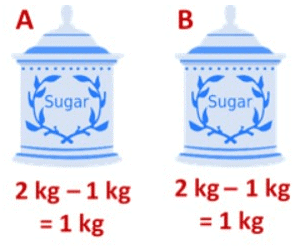 We see that the final quantity of sugar in both the jars remains the same.
We see that the final quantity of sugar in both the jars remains the same.
(4) Things which coincide with one another are equal.
Two pages of the same book coincide with each other and hence are equal. (5) The whole is greater than the part.
(5) The whole is greater than the part. Here, we see that a whole cake is greater than a slice (part) of the cake.
Here, we see that a whole cake is greater than a slice (part) of the cake.
(6) Things which are double of the same things are equal.
If x = 2y and z = 2y then x = z .
Suppose there are three jars of sugar, A, B, and C. Jars, A and B have an equal quantity of sugar, that is 2 kg and jar C has 1 kg of sugar.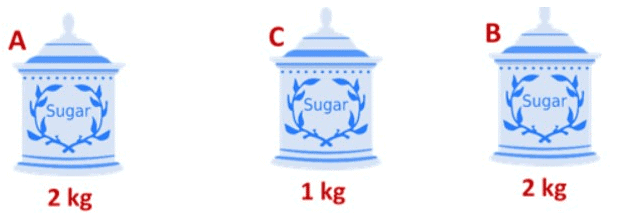 So, we see that the quantity of sugar in jar A and B is equal to twice the quantity of sugar in jar C or we can also say that both the jars A and B, have the same quantity of sugar as their quantities are also equal to twice the quantity of sugar in jar C.
So, we see that the quantity of sugar in jar A and B is equal to twice the quantity of sugar in jar C or we can also say that both the jars A and B, have the same quantity of sugar as their quantities are also equal to twice the quantity of sugar in jar C.
(7) Things that are halves of the same things are equal.
If x = y/2 and z = y/2 then x = z.
Suppose there are three jars of sugar, A, B, and C. Jars, A and B have an equal quantity of sugar, that is 1 kg and jar C has 2 kg of sugar.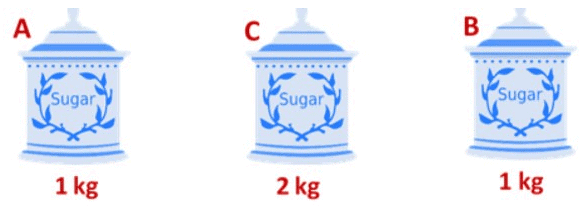 So, we see that the quantity of sugar in jar A and B is equal to half the quantity of sugar in jar C or we can also say that both the jars A and B, have the same quantity of sugar as their quantities are also equal to half the quantity of sugar in jar C.
So, we see that the quantity of sugar in jar A and B is equal to half the quantity of sugar in jar C or we can also say that both the jars A and B, have the same quantity of sugar as their quantities are also equal to half the quantity of sugar in jar C.
Example 1: Solve the equation y − 10 = 13 and state Euclid’s axioms used here.
y − 10 = 13
Adding 10 to both sides,
y − 10 + 10 = 13 + 10
y = 23
Here we have used Euclid’s axiom 2 which states that if equals are added to equals, the wholes are equals.
Example 2: In the given figure PT = QT, TR = TS, show that PR = QS. Write Euclid’s axiom to support this.
It is given that,
PT = QT Eq → 1
TR = TS Eq → 2
To show, PR = QS
Adding Eq 1 and Eq 2 we get,
PT + TR = QT + TS
PR = QS
Here, we have used Euclid’s axiom 2 which states that if equals are added to equals, the wholes are equals.
Example 3: In the given figure, we have BD = BC and AC = BC. State Euclid’s axiom to support this.
If BD = BC and AC = BC, then BD = AC
Here, we have used Euclid’s axiom 1 which states that things which are equal to the same thing are equal.
Example: Eric and David have the same weight. If both of them lose 5 kg weight, how will you compare their new weights?
Let x kg be the initial weight of both Eric and David.
On losing 5 kg, the weight of Eric and David will be (x − 5) kg.
According to Euclid’s axiom 3, if equals are subtracted from equals, the remainders are equal.
So, even after losing 5 kg, both Eric and David will have the same weight as their initial weights are also equal.
Euclid’s Five Postulates
Postulate 1: A straight line may be drawn from any one point to any other pointThis postulate states that at least one straight line passes through two distinct points, but it does not say that there cannot be more than one such line. However, Euclid has frequently assumed that there is a unique line joining two distinct points.
This result can be stated as an axiom given below:
Axiom: Given two distinct points, there is a unique line that passes through them. Here, we see that only one line, AB is passing through A and also through B. Now can you tell how many lines are passing through B and also through A?
Here, we see that only one line, AB is passing through A and also through B. Now can you tell how many lines are passing through B and also through A?
We see that the same line, i.e. AB is passing through B and A. The above statement is self-evident and so, it is called an axiom.
Postulate 2: A terminated line can be produced indefinitely.
Postulate 2 states that a line segment can be extended on either side to form a line.
Postulate 3: A circle can be drawn with any center and any radius.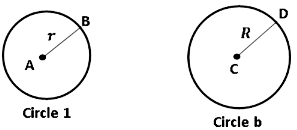 Here, AB = r is the radius of circle 1 and CD = R is the radius of circle 2.
Here, AB = r is the radius of circle 1 and CD = R is the radius of circle 2.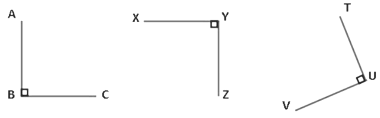
Postulate 4: All right angles are equal.
Here, ∠ABC = 90°
∠XYZ = 90°
∠TUV = 90°
So, all the right angles are equal.
Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles (180°), then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.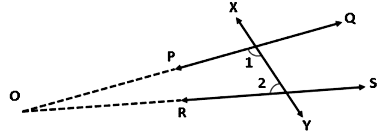 Suppose a straight line XY falls on two straight lines, PQ and RS in such a way that the interior angles ∠1 + ∠2 <180° on the left side of XY. The two lines PQ and RS, when produced indefinitely, will eventually intersect at point O on the left side of PQ.
Suppose a straight line XY falls on two straight lines, PQ and RS in such a way that the interior angles ∠1 + ∠2 <180° on the left side of XY. The two lines PQ and RS, when produced indefinitely, will eventually intersect at point O on the left side of PQ.
If we see the five postulates, we notice that postulate 5 is more complex than any other postulate. The postulates 1 through 4 are so simple and obvious that these are taken as ‘self - evident truths’. As it is not possible to prove these statements, they are accepted without any proof.
Euclid used his postulates and axioms to prove other results. Then using these results, he proved some more results by applying deductive reasoning. The statements that were proved are called propositions or theorem.
Euclid deduced 465 propositions in a logical chain using his axioms, postulates, definitions, and theorems proved earlier in the chain.
Example: If S, T, and U are three points on a line, and T lies between S and U, then prove that ST + TU = SU.
We see that SU coincides with ST + TU. According to Euclid’s axiom 4, things that coincide with one another are equal.
Therefore, SU = ST + TU
Now, in this solution, it has been assumed that there is a unique line passing through two points.
Example: Prove that an equilateral triangle can be constructed on any given line segment.
(1) We first draw a line segment PQ of length 1 cm.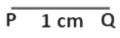 (2) Next, we draw a circle with point Q as center and QP as the radius. (Using Euclid’s postulate 3 – A circle can be drawn with any center and any radius)
(2) Next, we draw a circle with point Q as center and QP as the radius. (Using Euclid’s postulate 3 – A circle can be drawn with any center and any radius)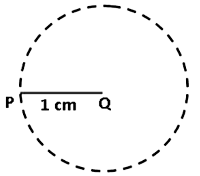 (3) Similarly, we draw another circle with P as center and radius equal to PQ.
(3) Similarly, we draw another circle with P as center and radius equal to PQ.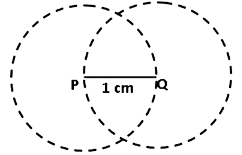 (4) The two circles meet at point R. Now draw the line segments, RP and RQ to form the ∆ RPQ.
(4) The two circles meet at point R. Now draw the line segments, RP and RQ to form the ∆ RPQ.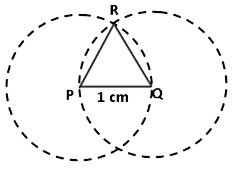 To prove:∆ RPQ is an equilateral triangle
To prove:∆ RPQ is an equilateral triangle
Here,
PQ = PR = 1 cm (Radii of the same circle)
PQ = QR = 1 cm (Radii of the same circle)
Using these two facts and Euclid’s axiom 1 (things which are equal to the same thing are equal) we conclude that,
PQ = PR = QR = 1 cm
Therefore, ∆ RPQ is an equilateral triangle as all the sides are equal.
Here, we see that Euclid has assumed that the two circles drawn with centers P and Q will meet each other at a point.
Theorem
Two distinct lines cannot have more than one point in common.
To prove: Lines l and m have only one point in common.
Proof: Let us suppose that the two lines intersect at two distinct points A and B which means that two lines are passing through two distinct points A and B.
According to the axiom, only one line can pass through two distinct points. Therefore, the assumption that the two lines can pass through two distinct points is wrong. So, two distinct lines cannot have more than one point in common.
Summary
Euclid’s definition
A point is that which has no part.
 A line is a breadthless length. The ends of a line are points and the straight line is a line which lies evenly with the points on itself.
A line is a breadthless length. The ends of a line are points and the straight line is a line which lies evenly with the points on itself.
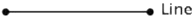 A surface is that which has length and breadth only. The edges of a surface are lines.Euclid’s axiom
A surface is that which has length and breadth only. The edges of a surface are lines.Euclid’s axiom
(i) Things which are equal to the same thing are equal.
Example: If
=
and
=
, then
=
(ii) If equals are added to equals, the wholes are equal.
Example: If x = y then x + z = y + z
(iii) If equals are subtracted from equals, the remainders are equal.
Example: If x = y then x − z = y − z
(iv) Things which coincide with one another are equal.
Example: Two pages of the same book
(v) The whole is greater than the part.
Example: A whole cake is greater than a slice (part) of the cake.
(vi) Things which are double of the same things are equal to one another.
Example: If x = 2y and z = 2y then x = z
(vii) Things which are halves of the same things are equal to one another.
Example: If x = y/2 and z = y/2 then x = z.
In geometry, a point, a line and a plane (or a plane surface) are considered as undefined terms.
- Euclid used the term ‘postulate’ for the assumptions that were specific to geometry.
- Common notions or axioms were assumptions used throughout mathematics and were not specifically linked to geometry.
Euclid’s postulate
Postulate 1: A straight line may be drawn from any one point to any other point.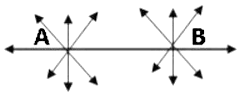 Postulate 2: A terminated line can be produced indefinitely.
Postulate 2: A terminated line can be produced indefinitely. Postulate 3: A circle can be drawn with any centre and any radius.
Postulate 3: A circle can be drawn with any centre and any radius. Postulate 4: All right angles are equal.
Postulate 4: All right angles are equal.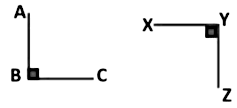 Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles (180°), then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles
Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles (180°), then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles Equivalent Versions of Euclid’s Fifth Postulate
Equivalent Versions of Euclid’s Fifth Postulate
‘For every line l and for every point P not lying on l, there exist a unique line m passing through P and parallel to l.
In Euclid’s era, mathematicians developed the concepts of a point, line, and plane from observing the space and solids around them. This led to a more abstract understanding of solid objects.
A solid has a shape, size, and position, and can be moved about. Therefore, a solid has three dimensions.
- Its edges are called surfaces.
|
40 videos|471 docs|57 tests
|
FAQs on Introduction to Euclid’s Geometry Class 9 Notes Maths Chapter 5
| 1. What are the key elements of Euclid's geometry introduced in Class 9? |  |
| 2. Can you provide some examples of Euclid's axioms? |  |
| 3. What are Euclid's Five Postulates and why are they important in geometry? |  |
| 4. How do Euclid's definitions, axioms, and postulates contribute to understanding geometry in Class 9? |  |
| 5. Why is it important to study Euclid's geometry in Class 9? |  |