Important Formulas: Polynomials | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Polynomial |

|
| Zeroes or roots of a polynomial |

|
| Relationship between Zeroes and Coefficients of a Polynomial |

|
| Division Algorithm |

|
| Identities of Algebra |

|
Polynomial
A polynomial is an algebraic expression in which the variables have non-integral exponents only.
Example- 3x2+ 4y + 2, 5x3+ 3x2 + 4x +2
Degree of a Polynomial
For a polynomial in one variable - The highest exponent on the variable in a polynomial is the degree of the polynomial.
Example: The degree of the polynomial x2+3x+4 is 3, as the highest power of x in the given expression is x2.
Types of Polynomials
- Number of terms
- Degree of the polynomial
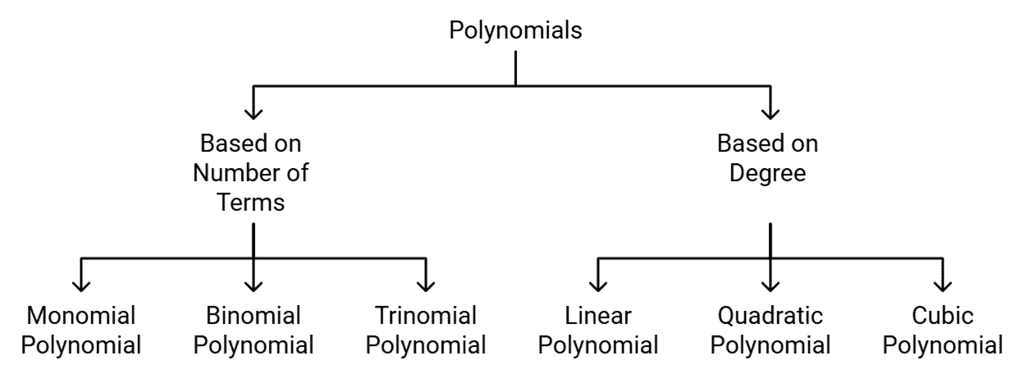 Types of Polynomials
Types of Polynomials
Types of Polynomials are based on the Number of terms:
- Monomial Polynomial – A polynomial with one term. Example: 3x, 8x2, 11xy
- Binomial – A polynomial that has two terms. Example: 6x2+x, 3x+4
- Trinomial – A polynomial that has three terms. Example: x2+4x+4
Types of Polynomials are based on the Degree of the Polynomial:
- Linear Polynomial - It is a polynomial of degree 1. It is of the form ax+ b where a & b are real numbers and a is not equal to 0.
- Quadratic Polynomial - It is a polynomial of degree 2. It is one of the form ax2+ bx + c where a, b & c are real numbers and a is not equal to 0.
- Cubic Polynomial - It is a polynomial of degree 3. It is one of the form ax3+ bx2 + cx+ d where a, b & c are real numbers and a is not equal to 0.
Zeroes or roots of a polynomial
It is that value of a variable at which polynomial P(x) becomes zero.
Example: if polynomial P(x) = x3-6x2+11x-6, Putting x = 1 one get P(1) = 0 then 1 is a zero of polynomial P(x).
- 0 may be a zero of a polynomial
- Linear polynomial can have at most one zero
- Quadratic polynomial can have at most two zeroes
- Cubic polynomial can have at most three zeroes
Geometrical Meaning of the Zeroes of a Polynomial
- The zeroes of a polynomial p(x) are the x-coordinates of the points, where the graph of y = p(x) intersects the x-axis.
- Number of zeroes of a polynomial is the number of times the graph intersects the x-axis.
Relationship between Zeroes and Coefficients of a Polynomial
- if α and β are the zeroes of the quadratic polynomial ax2 + bx+ c, then
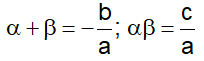
- If are the zeroes of the cubic polynomial ax3 + bx2 + cx+ d = 0,
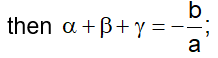
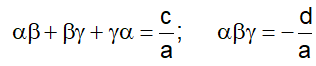
 |
Download the notes
Important Formulas: Polynomials
|
Download as PDF |
Division Algorithm
The division algorithm states that for any given polynomial p(x) and any non-zero polynomial g(x) there are polynomial q(x) are r(x) such that
p(x) = g(x) × q(x) + r(x)
Dividend = Divisor × Quotient + Remainder
Where r(x) = 0 or degree r(x) < degree g(x)
Number of Zeroes
A polynomial of degree n has at most n zeros.
- A linear polynomial has one zero,
- A quadratic polynomial has two zeros.
- A cubic polynomial has three zeros.
Factorisation of Polynomials
Quadratic polynomials can be factorized by splitting the middle term.
For example, consider the polynomial 2x2−5x+3
Splitting the middle term
The middle term in the polynomial is -5x
Sum = -5
Product = 6
Now, -5 can be expressed as (-2) + (-3) and -2 x -3 = 6
Putting the above value in the gven expression
2x2−5x+3 = 2x2−2x−3x+3
Identify the common factor
2x2−2x−3x+3 = 2x(x−1)−3(x−1)
Taking (x−1) as the common factor, this can be expressed as:
2x(x−1)−3(x−1)=(x−1)(2x−3)
Identities of Algebra
 Identities of Algebra
Identities of Algebra
|
40 videos|419 docs|51 tests
|
FAQs on Important Formulas: Polynomials - Mathematics (Maths) Class 9
| 1. What are the zeroes or roots of a polynomial? |  |
| 2. How does the relationship between zeroes and coefficients of a polynomial work? |  |
| 3. What is the Division Algorithm for polynomials? |  |
| 4. What are some important identities of algebra related to polynomials? |  |
| 5. What are some key formulas related to polynomials that students should remember? |  |

























