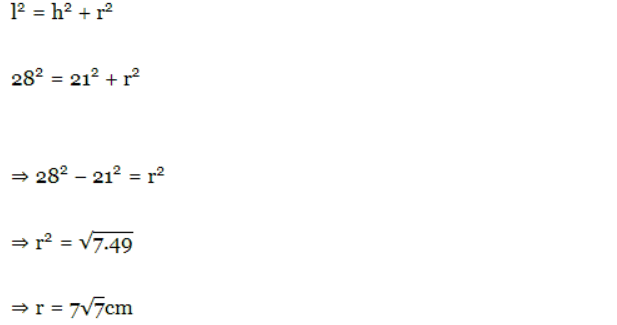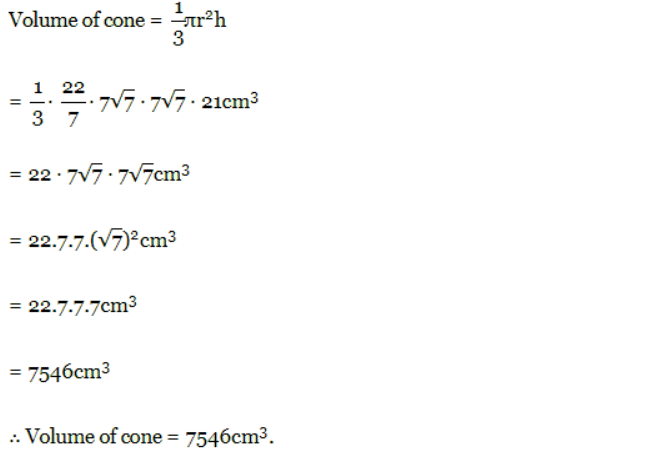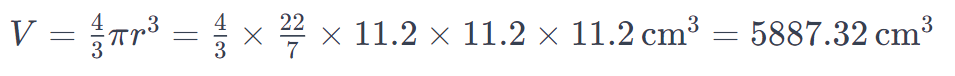Surface Area and Volumes Class 9 Notes Maths Chapter 12
Introduction
Understanding Surface Area and Volume
- Surface area is like the total paper to cover a 3D object.
- Volume is the space it occupies.
- Ever wondered how we measure the wrapping needed for a gift or the space inside a box?
 Wrapping Paper
Wrapping Paper
- It's how we quantify the outside and inside of shapes. So, how do we calculate these for different objects?
- Let's explore the answers by unravelling the mystery of surface area and delving into the roominess of volume!
- Suppose, we cut out a circle shape from a cardboard sheet.
- Then we cut many such circles identical to the first one and then pile them up in a single column. [Shown in the figure].
- Then the shape we obtained will be a 3-dimensional shape.
 By this process, we shall obtain some solid figures such as a cuboid and cube as shown below.
By this process, we shall obtain some solid figures such as a cuboid and cube as shown below. 
- All solid objects occupy some space and have three dimensions - length, breadth, and height or depth.
- Three-dimensional (3-d)shapes have four parts that set them apart from 2-d shapes viz. faces, vertices, edges, and volume.
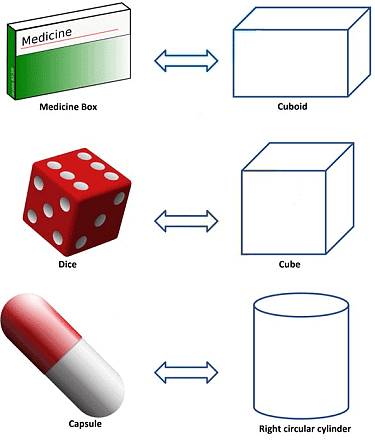
- Some real-life examples which resemble solid shapes as shown below.
Surface Area of Right Circular Cones
In this chapter, when we refer to a ‘cone’, we mean a ‘right circular cone’. These cones are three-dimensional shapes with a circular base that narrows down to a single point known as the apex or vertex. A familiar example is an ice cream cone.
The curved surface of a right circular cone is called the lateral surface, and the distance from the apex to the base is known as the height. It is important to grasp the properties of right circular cones to calculate their surface area and volume, which rely on their specific geometric features.
Activity: Construction of a Cone
 To grasp how a right circular cone is formed, follow these steps:
To grasp how a right circular cone is formed, follow these steps:
- Cut out a right-angled triangle ABC, with the right angle at B.
- Attach a thick string along one of the perpendicular sides, for example, AB.
- Rotate the triangle around the string. Notice the shape that forms — a cone.
- This shape is known as a right circular cone. Here, point A is the vertex, AB is the height, BC is the radius, and AC is the slant height of the cone.
Curved Surface Area of a Cone
Definition and Formula
The curved surface area (CSA) of a cone can be found using this formula:
- Curved Surface Area (CSA) = πrl
In this formula, r is the radius of the base, l is the slant height, and π can be approximated as 3.14 or 22/7.
Additional Information
- From the cone's cross-section, the relationship l² = r² + h² can be derived, where h is the height of the cone.
- If the cone's base is closed, a circular piece of paper with an area of πr² is needed, which adds to the total surface area.
Total Surface Area of a Cone = πrl + πr² = πr(l + r)
Example: Find the curved surface area of a right circular cone with a slant height of 10 cm and base radius of 7 cm.
Solution: Curved surface area = πrl = 22/7 × 7 × 10 = 220 cm²
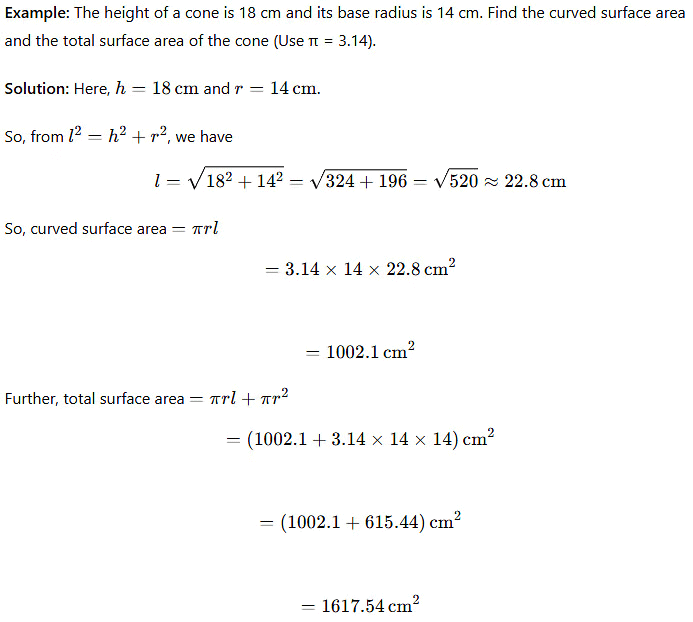
Total Surface Area of a Cone
Definition
The total surface area of a cone is the total of its curved surface area (CSA) and the area of its base. The formulas are as follows:
Curved Surface Area (CSA)
- CSA = πrl
- where r is the radius of the base and l is the slant height of the cone.
Area of the Base
- Area of base = πr²
Total Surface Area
- Total Surface Area = CSA + Area of base = πrl + πr² = πr(l + r)
Example: The height of a cone is 16 cm and its base radius is 12 cm. Find the curved surface area and the total surface area of the cone (Use π = 3.14).
Solution:
- Here, h = 16 cm and r = 12 cm.
- Using the formula l² = h² + r², we find:
- l = √(16² + 12²) = √(256 + 144) = √400 = 20 cm
- Curved surface area = πrl = 3.14 × 12 × 20 = 753.6 cm²
- Total surface area = πrl + πr² = 753.6 + 3.14 × 12 × 12 = 753.6 + 452.16 = 1205.76 cm²
Surface Area of Sphere
Spheres are completely round three-dimensional shapes, similar to balls or globes.
Every point on a sphere's surface is the same distance from its centre.
Examples include:
- A basketball
- The nearly spherical shape of the Earth
Spheres do not have edges or corners.

Surface Area Calculation
The surface area of a sphere is calculated as:
Surface Area=4πr2
Here, r is the sphere's radius.
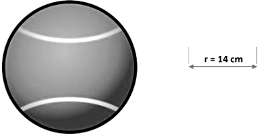
Example: Find the surface area of a tennis ball of radius 14 cm.
Clearly, the tennis ball is in the form of a sphere.
Here, the radius of the sphere is 14 cm.
We know that,
Surface Area of the sphere =4πr2.
Therefore, the Surface Area of a tennis ball =4πr2.
= 4 × 22/7 × (14 cm)2.
= 4 × 22/7 × 14cm × 14 cm.
= 4 × 22 × 2cm × 14 cm.
= 2464 cm2.
Hence, the Surface area of the tennis ball is 2464 cm2.
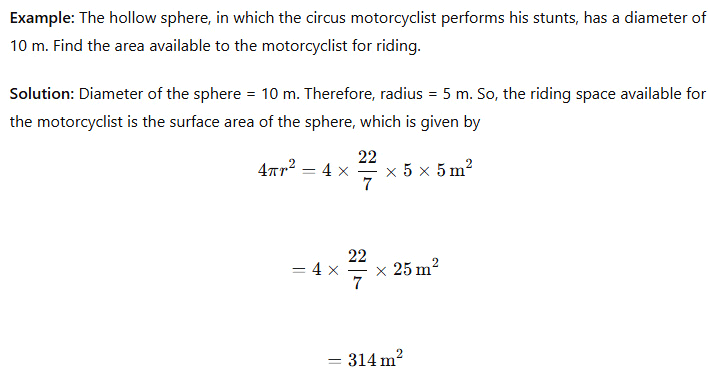
Note: A sphere doesn't have separate curved and total surface areas because its entire surface is curved. In other words, there are no flat or planar sections on a sphere. The term "surface area" for a sphere typically refers to the total surface area, which includes both the curved surface area and the area of the sphere's base (which is also curved).
Surface Area of Hemisphere
A hemisphere, which is half of a sphere, has a surface area calculated as 3πr².
Surface Area of Hemisphere= 3/2×4πr2=3πr2
- Imagine a sphere cut directly in half with a plane through its centre.
- This creates two equal parts, known as a hemisphere (since 'hemi' means 'half'). A hemisphere consists of a curved face and a flat base.
- The curved surface area of a hemisphere is half of the sphere's surface area, which is 1/2 of 4πr².
Curved Surface Area of a Hemisphere = 2πr²
Here, r represents the radius of the sphere from which the hemisphere is derived. The total surface area of the hemisphere, combining both faces, is calculated as 2πr² + πr². Thus, the Total Surface Area of a Hemisphere = 3πr².
Example: Calculate the curved surface area and total surface area of a hemisphere with a radius of 7 cm.
Solution: Consider a half slice of watermelon, shaped like a hemisphere with a radius of 7 cm. The curved surface area is calculated as follows:
Curved Surface Area of Hemisphere = 2πr² = 2 × (22/7) × (7 cm)² = 2 × (22/7) × 49 cm² = 308 cm².
Thus, the Curved Surface area of the watermelon slice is 308 cm².
Furthermore, the total surface area of a hemisphere is computed as:
Total Surface Area of Hemisphere = 3πr² = 3 × (22/7) × (7 cm)² = 3 × (22/7) × 49 cm² = 462 cm².
Therefore, the total surface area of the half slice of watermelon is 462 cm².
What is Volume?
Volume refers to the amount of space occupied by a three-dimensional object. It is a measure of how much "stuff" or substance an object can hold. The concept of volume is often applied to various geometric shapes, such as cubes, spheres, cylinders, and cones.
Volume of a Cone
The volume (V) of a cone is calculated using the formula:
V= 1/3πr2h
Here, r is the base radius, and h is the height of the cone.
Example:
Given the height (h) and slant height (l) of a cone as 21 cm and 28 cm respectively, find the volume.
Solution: Slant height (l) = 28cm; Height of cone (h) = 21cm ; Let radius of cone = r cm
we know that,
Volume of a Sphere
The volume (V) of a sphere can be understood by thinking about how much water the sphere pushes aside when it is put in water. This basic idea is very important. The volume of a sphere can be calculated using the formula:
V = 4/3 × π × r3
In this formula, r stands for the radius of the sphere.
Example: Find the volume of a sphere with a radius of 11.2 cm.
Solution: To calculate the volume of a sphere with a radius of 11.2 cm, we can use the formula:
Volume of a Hemisphere
The volume of a hemisphere is half of a sphere.
You can calculate the volume of a hemisphere using the formula:
Volume of a Hemisphere = (2/3)πr³
In this formula:
- r is the radius of the hemisphere, and
- π is a mathematical constant, roughly equal to 3.14159.
The volume of a sphere is given by Volume of a Sphere = (4/3)πr³, where r is the radius of the sphere.
Since a hemisphere is half of a sphere, its volume is half the volume of a sphere.
Example: A dome of a building is shaped like a hemisphere. The cost to whitewash it from the inside was Rs. 4989.60. If the cost to whitewash is Rs. 20 per square metre, calculate:
(i) The inside surface area of the dome
(ii) The volume of the air inside the dome
Solution: (i) The cost of whitewashing the dome from the inside is Rs. 4989.60.The cost to whitewash 1m² is Rs. 20.
The curved surface area of the inner side of the dome is:
Curved Surface Area = Total Cost / Cost per m² = 4989.60 / 20 = 249.48 m²
(ii) Let the inner radius of the dome be r.
The curved surface area of the inner side of the dome is 249.48 m² (from (i)).
The formula for the curved surface area (CSA) of a hemisphere is:
CSA = 2πr²
So, we have:
2πr = 249.48
2 × (22/7) × r² = 249.48
r² = (249.48 × 7) / (2 × 22)
r² = 39.69
r = 6.3
Thus, the radius is 6.3 m.
The volume of air inside the given dome = Volume of hemispherical dome
Using the formula, the volume of the hemisphere is:
Volume = (2/3)πr³
= (2/3) × (22/7) × 6.3 × 6.3 × 6.3
= 523.9 (approx.)
The volume of air inside the dome is approximately 523.9 m³.
|
40 videos|471 docs|57 tests
|
FAQs on Surface Area and Volumes Class 9 Notes Maths Chapter 12
| 1. What is the formula to calculate the curved surface area of a right circular cone? |  |
| 2. How do you calculate the total surface area of a cone? |  |
| 3. What is the formula for the surface area of a sphere? |  |
| 4. How is the volume of a sphere calculated? |  |
| 5. What is the difference between the volume of a hemisphere and the volume of a sphere? |  |