Number Base Conversion | Digital Circuits - Electronics and Communication Engineering (ECE) PDF Download
Introduction
In our previous section, we learned different types of number systems such as binary, decimal, octal, and hexadecimal. In this part of the tutorial, we will learn how we can change a number from one number system to another number system.
As, we have four types of number systems so each one can be converted into the remaining three systems. There are the following conversions possible in Number System
- Binary to other Number Systems.
- Decimal to other Number Systems.
- Octal to other Number Systems.
- Hexadecimal to other Number Systems.
Binary to other Number Systems
There are three conversions possible for binary number, i.e., binary to decimal, binary to octal, and binary to hexadecimal. The conversion process of a binary number to decimal differs from the remaining others. Let's take a detailed discussion on Binary Number System conversion.
Binary to Decimal Conversion
The process of converting binary to decimal is quite simple. The process starts from multiplying the bits of binary number with its corresponding positional weights. And lastly, we add all those products.
Let's take an example to understand how the conversion is done from binary to decimal.
Example 1: (10110.001)2
We multiplied each bit of (10110.001)2 with its respective positional weight, and last we add the products of all the bits with its weight.
(10110.001)2 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (0 × 20) + (0 × 2-1) + (0 × 2-2) + (1 × 2-3)
(10110.001)2 = (1 × 16) + (0 × 8) + (1 × 4) + (1 × 2) + (0 × 1) + (0 × 1⁄2) + (0 × 1⁄4) + (1 × 1⁄8)
(10110.001)2 = 16 + 0 + 4 + 2 + 0 + 0 + 0 + 0.125
(10110.001)2 = (22.125 )10
Binary to Octal Conversion
The base numbers of binary and octal are 2 and 8, respectively. In a binary number, the pair of three bits is equal to one octal digit. There are only two steps to convert a binary number into an octal number which are as follows:
- In the first step, we have to make the pairs of three bits on both sides of the binary point. If there will be one or two bits left in a pair of three bits pair, we add the required number of zeros on extreme sides.
- In the second step, we write the octal digits corresponding to each pair.
Example 1: (111110101011.0011)2
1. Firstly, we make pairs of three bits on both sides of the binary point.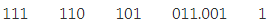
On the right side of the binary point, the last pair has only one bit. To make it a complete pair of three bits, we added two zeros on the extreme side.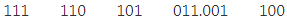
2. Then, we wrote the octal digits, which correspond to each pair.
(111110101011.0011)2 = (7653.14)8
Binary to Hexadecimal Conversion
The base numbers of binary and hexadecimal are 2 and 16, respectively. In a binary number, the pair of four bits is equal to one hexadecimal digit. There are also only two steps to convert a binary number into a hexadecimal number which are as follows:
- In the first step, we have to make the pairs of four bits on both sides of the binary point. If there will be one, two, or three bits left in a pair of four bits pair, we add the required number of zeros on extreme sides.
- In the second step, we write the hexadecimal digits corresponding to each pair.
Example 1: (10110101011.0011)2
1. Firstly, we make pairs of four bits on both sides of the binary point.
111 1010 1011.0011
On the left side of the binary point, the first pair has three bits. To make it a complete pair of four bits, add one zero on the extreme side.
0111 1010 1011.0011
2. Then, we write the hexadecimal digits, which correspond to each pair.
(011110101011.0011)2 = (7AB.3)16
Decimal to other Number System
The decimal number can be an integer or floating-point integer. When the decimal number is a floating-point integer, then we convert both part (integer and fractional) of the decimal number in the isolated form(individually). There are the following steps that are used to convert the decimal number into a similar number of any base 'r'.
- In the first step, we perform the division operation on integer and successive part with base 'r'. We will list down all the remainders till the quotient is zero. Then we find out the remainders in reverse order for getting the integer part of the equivalent number of base 'r'. In this, the least and most significant digits are denoted by the first and the last remainders.
- In the next step, the multiplication operation is done with base 'r' of the fractional and successive fraction. The carries are noted until the result is zero or when the required number of the equivalent digit is obtained. For getting the fractional part of the equivalent number of base 'r', the normal sequence of carrying is considered.
Decimal to Binary Conversion
For converting decimal to binary, there are two steps required to perform, which are as follows:
- In the first step, we perform the division operation on the integer and the successive quotient with the base of binary(2).
- Next, we perform the multiplication on the integer and the successive quotient with the base of binary(2).
Example 1: (152.25)10
Step 1: Divide the number 152 and its successive quotients with base 2.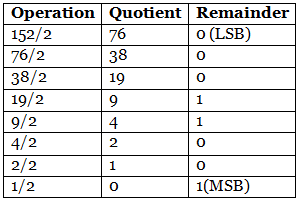 (152)10 = (10011000)2
(152)10 = (10011000)2
Step 2: Now, perform the multiplication of 0.27 and successive fraction with base 2.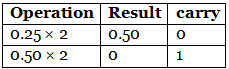 (0.25)10 = (.01)2
(0.25)10 = (.01)2
Decimal to Octal Conversion
For converting decimal to octal, there are two steps required to perform, which are as follows:
- In the first step, we perform the division operation on the integer and the successive quotient with the base of octal(8).
- Next, we perform the multiplication on the integer and the successive quotient with the base of octal(8).
Example 1: (152.25)10
Step 1: Divide the number 152 and its successive quotients with base 8.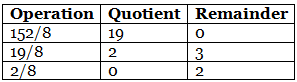 (152)10 = (230)8
(152)10 = (230)8
Step 2: Now perform the multiplication of 0.25 and successive fraction with base 8.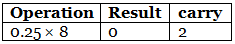 (0.25)10 = (2)8
(0.25)10 = (2)8
So, the octal number of the decimal number 152.25 is 230.2
Decimal to Hexadecimal Conversion
For converting decimal to hexadecimal, there are two steps required to perform, which are as follows:
- In the first step, we perform the division operation on the integer and the successive quotient with the base of hexadecimal (16).
- Next, we perform the multiplication on the integer and the successive quotient with the base of hexadecimal (16).
Example 1: (152.25)10
Step 1: Divide the number 152 and its successive quotients with base 8. (152)10 = (98)16
(152)10 = (98)16
Step 2: Now perform the multiplication of 0.25 and successive fraction with base 16.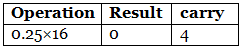 (0.25)10 = (4)16
(0.25)10 = (4)16
So, the hexadecimal number of the decimal number 152.25 is 98.4.
Octal to other Number System
Like binary and decimal, the octal number can also be converted into other number systems. The process of converting octal to decimal differs from the remaining one. Let's start understanding how conversion is done.
Octal to Decimal Conversion
The process of converting octal to decimal is the same as binary to decimal. The process starts from multiplying the digits of octal numbers with its corresponding positional weights. And lastly, we add all those products.
Let's take an example to understand how the conversion is done from octal to decimal.
Example 1: (152.25)8
Step 1: We multiply each digit of 152.25 with its respective positional weight, and last we add the products of all the bits with its weight.
(152.25)8 = (1 × 82) + (5 × 81) + (2 × 80) + (2 × 8 - 1) + (5 × 8 - 2)
(152.25)8 = 64 + 40 + 2 + (2 × 1⁄8) + (5 × 1⁄64)
(152.25)8 = 64 + 40 + 2 + 0.25 + 0.078125
(152.25)8 = 106.328125
So, the decimal number of the octal number 152.25 is 106.328125
Octal to Binary Conversion
The process of converting octal to binary is the reverse process of binary to octal. We write the three bits binary code of each octal number digit.
Example 1: (152.25)8
We write the three-bit binary digit for 1, 5, 2, and 5.
(152.25)8 = (001101010.010101)2
So, the binary number of the octal number 152.25 is (001101010.010101)2
Octal to hexadecimal conversion
For converting octal to hexadecimal, there are two steps required to perform, which are as follows:
- In the first step, we will find the binary equivalent of number 25.
- Next, we have to make the pairs of four bits on both sides of the binary point. If there will be one, two, or three bits left in a pair of four bits pair, we add the required number of zeros on extreme sides and write the hexadecimal digits corresponding to each pair.
Example 1: (152.25)8
Step 1: We write the three-bit binary digit for 1, 5, 2, and 5.
(152.25)8 = (001101010.010101)2
So, the binary number of the octal number 152.25 is (001101010.010101)2
Step 2: 1. Now, we make pairs of four bits on both sides of the binary point.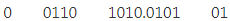
On the left side of the binary point, the first pair has only one digit, and on the right side, the last pair has only two-digit. To make them complete pairs of four bits, add zeros on extreme sides.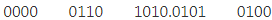
2. Now, we write the hexadecimal digits, which correspond to each pair.
(0000 0110 1010.0101 0100)2= (6A.54)16
Hexa-decimal to other Number System
Like binary, decimal, and octal, hexadecimal numbers can also be converted into other number systems. The process of converting hexadecimal to decimal differs from the remaining one. Let's start understanding how conversion is done.
Hexa-decimal to Decimal Conversion
The process of converting hexadecimal to decimal is the same as binary to decimal. The process starts from multiplying the digits of hexadecimal numbers with its corresponding positional weights. And lastly, we add all those products.
Let's take an example to understand how the conversion is done from hexadecimal to decimal.
Example 1: (152A.25)16
Step 1: We multiply each digit of 152A.25 with its respective positional weight, and last we add the products of all the bits with its weight.
(152A.25)16 = (1 × 163) + (5 × 162) + (2 × 161) + (A × 160) + (2 × 16-1) + (5 × 16-2)
(152A.25)16 = (1 × 4096) + (5 × 256) + (2 × 16) + (10 × 1) + (2 × 16-1) + (5 × 16-2)
(152A.25)16 = 4096 + 1280 + 32 + 10 + (2 ×1 ⁄16) + (5 × 1⁄256)
(152A.25)16 = 5418 + 0.125 + 0.125
(152A.25)16 = 5418.14453125
So, the decimal number of the hexadecimal number 152A.25 is 5418.14453125
Hexadecimal to Binary Conversion
The process of converting hexadecimal to binary is the reverse process of binary to hexadecimal. We write the four bits binary code of each hexadecimal number digit.
Example 1: (152A.25)16
We write the four-bit binary digit for 1, 5, A, 2, and 5.
(152A.25)16 = (0001 0101 0010 1010.0010 0101)2
So, the binary number of the hexadecimal number 152.25 is (1010100101010.00100101)2
Hexadecimal to Octal Conversion
For converting hexadecimal to octal, there are two steps required to perform, which are as follows:
- In the first step, we will find the binary equivalent of the hexadecimal number.
- Next, we have to make the pairs of three bits on both sides of the binary point. If there will be one or two bits left in a pair of three bits pair, we add the required number of zeros on extreme sides and write the octal digits corresponding to each pair.
Example 1: (152A.25)16
Step 1: We write the four-bit binary digit for 1, 5, 2, A, and 5.
(152A.25)16 = (0001 0101 0010 1010.0010 0101)2
So, the binary number of hexadecimal number 152A.25 is (0011010101010.010101)2
Step 2: Then, we make pairs of three bits on both sides of the binary point.
001 010 100 101 010.001 001 010
Then, we write the octal digit, which corresponds to each pair.
(001010100101010.001001010)2 = (12452.112)8
So, the octal number of the hexadecimal number 152A.25 is 12452.112
|
75 videos|188 docs|70 tests
|
















