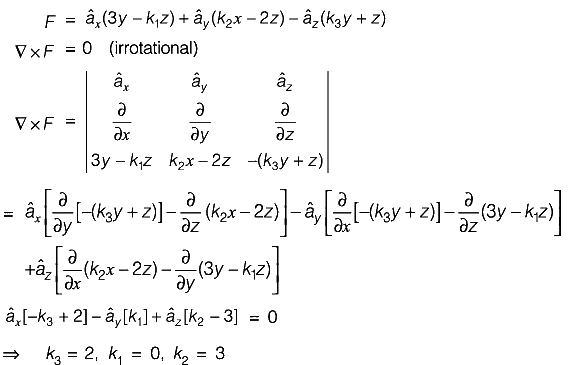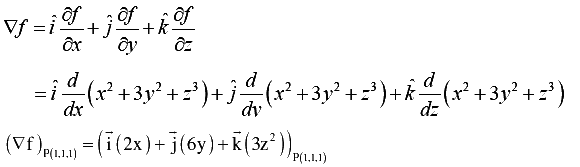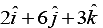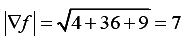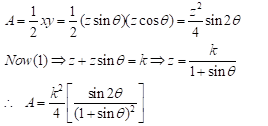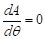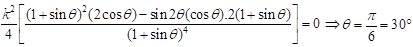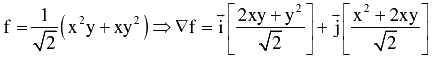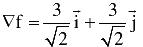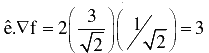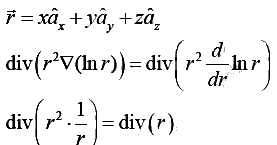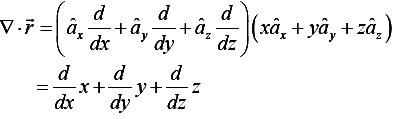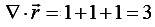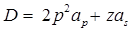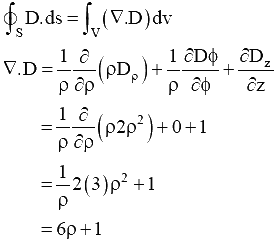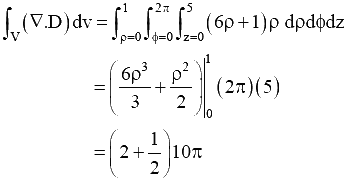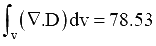Vector Calculus: PYQ | Engineering Mathematics - Engineering Mathematics PDF Download
Q.1. If the vector function 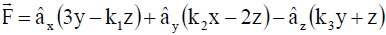 is irrotational, then the values of the constants k1, k2 and k3 respectively, are
is irrotational, then the values of the constants k1, k2 and k3 respectively, are
(a) 0.3, –2.5, 0.5
(b) 0.0, 3.0, 2.0
(c) 0.3, 0.33, 0.5
(d) 4.0, 3.0, 2.0
Correct Answer is option (b)
Q.2. The magnitude of the gradient for the function f(x, y, z) = x2 + 3y2 + z3 at the point (1, 1, 1) is
(a) 7
(b) 9
(c) 12
(d) 5
Correct Answer is option (a)
Gradient of function f is
Gradient at P(1, 1, 1) is =
Magnitude of gradient
=
Q.3. For a right angled triangle, if the sum of the lengths of the hypotenuse and a side is kept constant, in order to have maximum area of the triangle, the angle between the hypotenuse and the side is________(o)
(a) 12
(b) 36
(c) 30
(d) 45
Correct Answer is option (c)
Le
x (opposite side
y (adjacent side
z (hypotenuse) of a right angled triangle
Given Z + y = K(constant) ......(1) and angle between them say θ then Area,
In order to have maximum area,
⇒
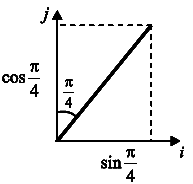
Q.4. The directional derivative of 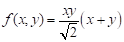 in the direction of the unit vector at an angle of π/4 with y-axis at point (1,1), is given by _____.
in the direction of the unit vector at an angle of π/4 with y-axis at point (1,1), is given by _____.
(a) 3
(b) 5
(c) 8
(d) 4
Correct Answer is option (a)
Gradient of function f is :
Gradient at (1, 1),
So, representation of unit vector in cartesion is,
=
∴ Directions of derivative =
Q.5. If 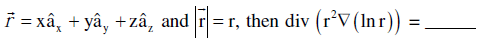
(a) 1
(b) 2
(c) 3
(d) 4
Correct Answer is option (c)
Given , the vector field
Divergence of Vectoris
Q.6. A vector field D = 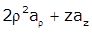 exists inside a cylindrical region enclosed by the surfaces p = 1, z = 0 and z = 5. Let S be the surface bounding this cylindrical region. The surface integral of this field on S
exists inside a cylindrical region enclosed by the surfaces p = 1, z = 0 and z = 5. Let S be the surface bounding this cylindrical region. The surface integral of this field on S 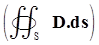 is _____. (Fill in the Blank Type Question)
is _____. (Fill in the Blank Type Question)
In the given vector field,
By using divergence theorem
|
65 videos|129 docs|94 tests
|