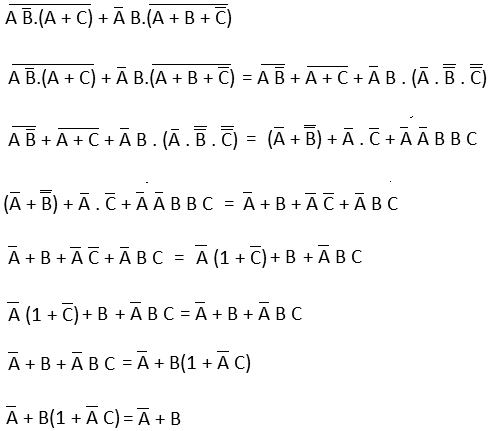De-Morgan's Theorem | Digital Circuits - Electronics and Communication Engineering (ECE) PDF Download
What is De-Morgan's Theorem?
A famous mathematician De-Morgan invented the two most important theorems of boolean algebra. The De-Morgan's theorems are used for mathematical verification of the equivalency of the NOR and negative-AND gates and the negative-OR and NAND gates. These theorems play an important role in solving various boolean algebra expressions. In the below table, the logical operation for each combination of the input variable is defined.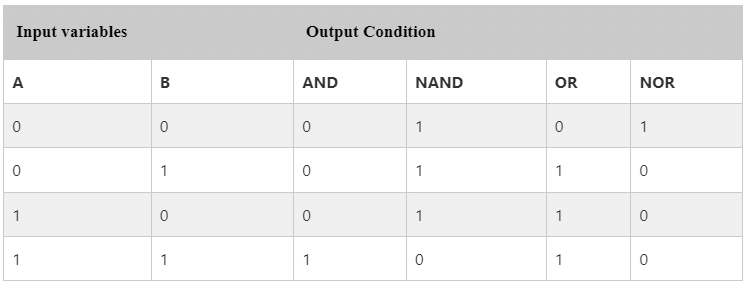 The rules of De-Morgan's theorem are produced from the Boolean expressions for OR, AND, and NOT using two input variables x and y. The first theorem of De-morgan's says that if we perform the AND operation of two input variables and then perform the NOT operation of the result, the result will be the same as the OR operation of the complement of that variable. The second theorem of De-Morgan says that if we perform the OR operation of two input variables and then perform the NOT operation of the result, the result will be the same as the AND operation of the complement of that variable.
The rules of De-Morgan's theorem are produced from the Boolean expressions for OR, AND, and NOT using two input variables x and y. The first theorem of De-morgan's says that if we perform the AND operation of two input variables and then perform the NOT operation of the result, the result will be the same as the OR operation of the complement of that variable. The second theorem of De-Morgan says that if we perform the OR operation of two input variables and then perform the NOT operation of the result, the result will be the same as the AND operation of the complement of that variable.
De-Morgan's First Theorem
According to the first theorem, the complement result of the AND operation is equal to the OR operation of the complement of that variable. Thus, it is equivalent to the NAND function and is a negative-OR function proving that (A.B)' = A'+B' and we can show this using the following table.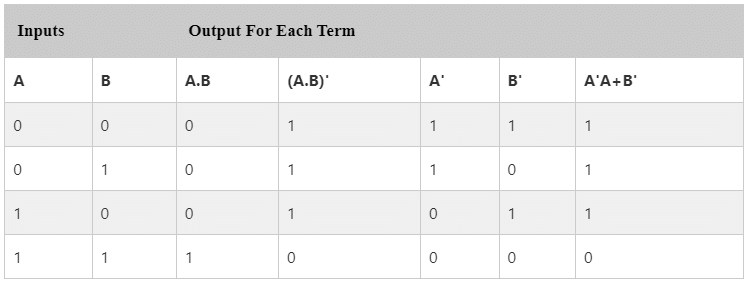
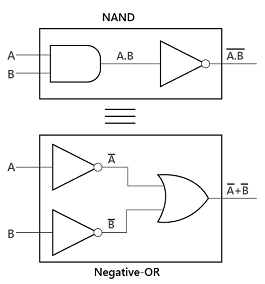
De-Morgan's Second Theorem
According to the second theorem, the complement result of the OR operation is equal to the AND operation of the complement of that variable. Thus, it is the equivalent of the NOR function and is a negative-AND function proving that (A+B)' = A'.B' and we can show this using the following truth table.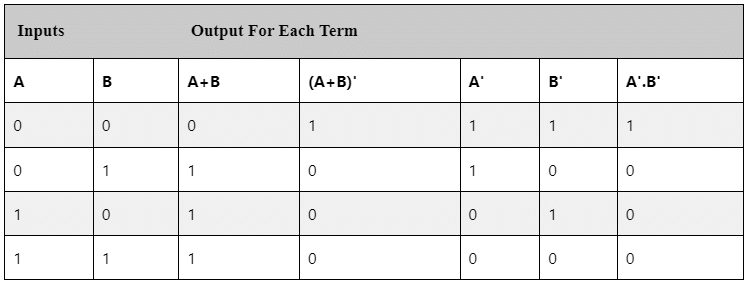
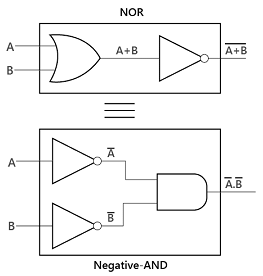
Let's take some examples in which we take some expressions and apply DeMorgan's theorems.
Example 1: (A . B . C)'
(A . B . C)' = A' + B' + C'
Example 2: (A + B + C)'
(A + B + C)' = A' . B' . C
Example 3: ((A + BC')' + D( E+ F')')'
For applying the DeMorgan's theorem on this expression, we have to follow the following expressions:
(1) In complete expression, first, we find those terms on which we can apply the De-Morgan's theorem and treat each term as a single variable.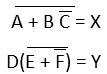 So,
So,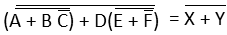 (2) Next, we apply De-Morgan's first theorem. So,
(2) Next, we apply De-Morgan's first theorem. So, (3) Next, we use rule number 9, i.e., (A=(A')') for canceling the double bars.
(3) Next, we use rule number 9, i.e., (A=(A')') for canceling the double bars. (4) Next, we apply DeMorgan's second theorem. So,
(4) Next, we apply DeMorgan's second theorem. So, (5) Again apply rule number 9 to cancel the double bar
(5) Again apply rule number 9 to cancel the double bar Now, this expression has no term in which we can apply any rule or theorem. So, this is the final expression.
Now, this expression has no term in which we can apply any rule or theorem. So, this is the final expression.
Example: (AB'.(A + C))'+ A'B.(A + B + C')'
|
6 videos|77 docs|52 tests
|