Linear Equations in One Variable | Mathematics for ACT PDF Download

A linear equation in one variable is the basic equation used to represent and solve for an unknown quantity. It can be easily represented graphically and it is always a straight line. The linear equation is an easy way of representing a math statement. Any variable or symbol can be used to represent unknown quantities but generally, a variable 'x' is used to represent the unknown quantity in the linear equation in one variable. 

What is Linear Equation in One Variable?

• The linear equation in one variable is an equation which is expressed in the form of ax+b = 0, where a and b are two integers, and x is a variable and has only one solution.
  
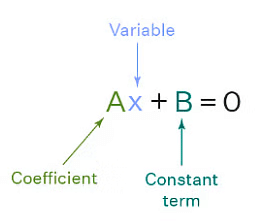
• For example, 2x+3=8 is a linear equation having a single variable in it. Therefore, this equation has only one solution, which is x = 5/2. 
• Whereas if we speak about linear equation in two variables, it has two solutions.
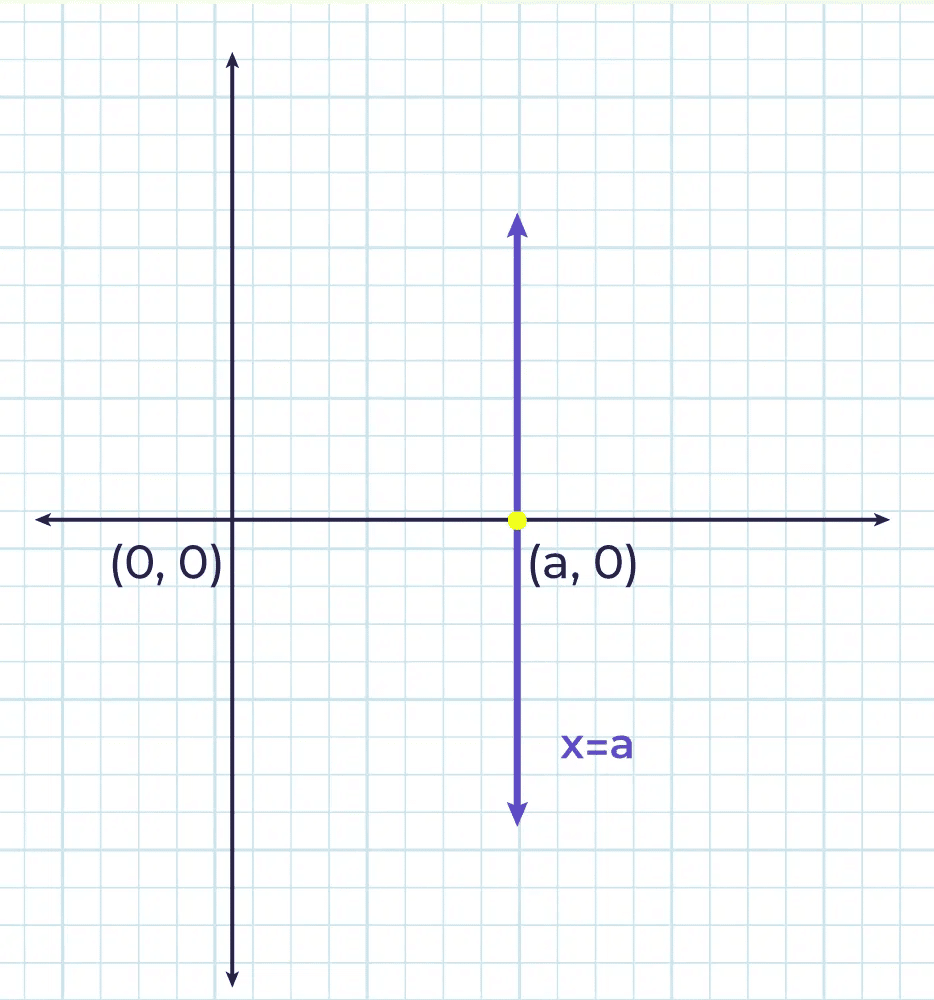  Graph of Linear Equation in One Variable
• This equation has only one solution. A few examples are:
  3x = 1
  22x-1=0
  4x+9=-11
• When it is drawn on a graph, it appears to be a straight line either horizontally or vertically.

Solving Linear Equation in One Variable

For solving an equation having only one variable, the following steps are followed

• Step 1: Using LCM, clear the fractions if any.
• Step 2: Simplify both sides of the equation.
• Step 3: Isolate the variable.
• Step 4: Verify your answer.

Example: Solve 5x – 9 = -3x + 19

Step 1: 

• Transpose all the variables on one side of the equation. By transpose, we mean to shift the variables from one side of the equation to the other side of the equation. In the method of transposition, the operation on the operand gets reversed.
• In the equation 5x – 9 = -3x + 19, we transpose -3x from the right-hand side to the left-hand side of the equality, the operation gets reversed upon transposition and the equation becomes:
  5x – 9 +3x = 19
  ⇒ 8x -9 = 19

Step 2: 

• Similarly transpose all the constant terms on the other side of the equation as below:
  8x -9 = 19
  ⇒ 8x = 19 + 9
  ⇒ 8x = 28

Step 3: 

• Divide the equation with 8 on both sides of the equality.
  8x/8 = 28/8
  ⇒ x = 28/8
• If we substitute x = 28/8 in the equation 5x – 9 = -3x + 19, we will get 9 = 9, thereby satisfying the equality and giving us the required solution.

Linear Equation in One Variable vs Non-Linear Equations

• Apart from linear equations in one variable, we have other non-linear equations, which have numerous applications in geometry, trigonometry, and calculus. 
• Linear equations in one variable are single-degree equations and are represented as a line on a coordinate plane. 
• A non-linear equation on the other hand is a curve or non-linear representation on the coordinate axis. A nonlinear equation is of a higher degree. 
• Few examples of non-linear equations are the equation of curves such as a circle, parabola, ellipse, hyperbola.
• Some of the samples of linear equations are x = 5, 3x + 7 = 9, 4x + 2y = 11. 
  Some of the examples of non-linear equations are the equation of a circle - x² + y² = 25, equation of a elipse - x²/9 + y²/16 = 1, equation of a hyperbola - x² /16 - y²/ 25 = 1. 

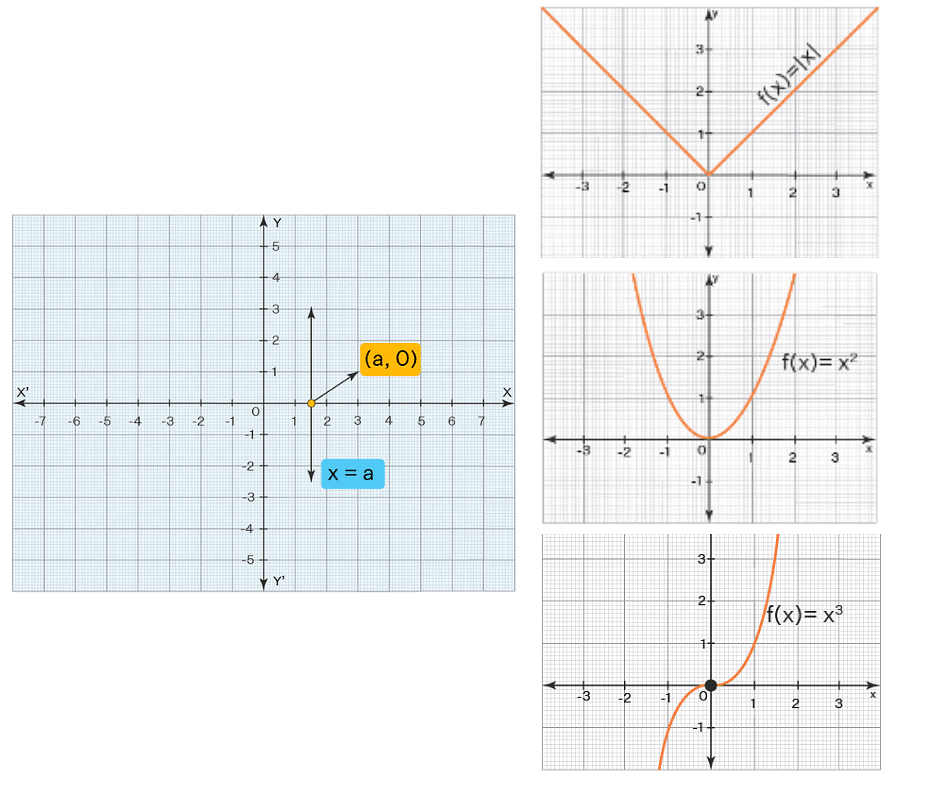Linear Equation in One Variable VS Non Linear Equation

Important Points

The following points help us in clearly summarizing the concepts involved in linear equations in one variable.

• The degree of the variable in linear equations should be exactly equal to one.
• The graph of a linear equation in one variable is a straight line, either horizontal or vertical.
• The solution of a linear equation in one variable is unaffected if any number is added, subtracted, multiplied, or divided on both sides of the equation.

Solved Examples

Example 1: Twenty years ago, Mikkel's age was one-third of what it is now. What is Mikkel's present age?
Solution: We can write the given information by using a linear equation in one variable. Let Mikkel's present age be x years. Twenty years ago, Mikkel's age was (x-20) years. According to the given information, x - 20= x/3
3(x - 20)= x
3x - 60= x
3x - x= 60
2x= 60
x= 60/2
x= 30
Therefore the present age of Mikkel is 30 years.

Example 2: David worked as a stenographer. In June, he was paid $50 per day. However, $10 per day was deducted for the days he remained absent. He received $900 for the number of days he worked. How many days did he work?
Solution: Let the number of days he worked be x days. Hence, the number of days he did not work will be = 30 - x. He was paid $50 for each day he worked and $10 was deducted for each day he did not work. At the end of the month, he received $900. According to the given information, we can form a linear equation in one variable as, 50(x) - 10(30 - x) = 900
50x - 300 + 10x = 900
60x = 900 + 300
x = 1200/60
x= 20
Therefore David worked for 20 days.

Example 3: Find the perimeter of the square whose side length x units is given in the form of an equation as 2x/3- 5/6 = 0
Solution: Given, the side-length of the square is 2x/3- 5/6=0. It is in the form of a linear equation in one variable which is x. First, we need to solve this equation to find the value of x.
2x/3- 5/6=0
2x/3- 5/6 + 5/6=0+ 5/6 (adding 5/6 on both the sides)
2x/3= 5/6
x = 5/6 × 3/2
x = 5/4 units
Hence, the side length of the square is 5/4 units. Now, to find the perimeter of the square, we need to multiply the side length by 4.
The perimeter of a square = 5/4 × 4=5 units.
Therefore the perimeter of the square is 5 units.

Example 4: The length of the legs of an isosceles triangle is 4 meters more than its base. If the Perimeter of the triangle is 44 meters, find the lengths of the sides of the triangle.
Solution: Let us assume the base measures ‘x’ meter. Hence, each of the legs measure y = (x + 4) meters.
The Perimeter of a triangle is the sum of the three sides.
The equations are formed and solved as follows:
x + 2(x + 4) = 44
x + 2x + 8 = 44
3x + 8 = 44
3x = 44 – 8 = 36
3x = 36
x = 36/3
x = 12
The length of the base is solved as 12 meters. Hence, each of the two legs measure 16 meters.