Van der Waals equation and the theorem of corresponding states | Physical Chemistry PDF Download

Introduction

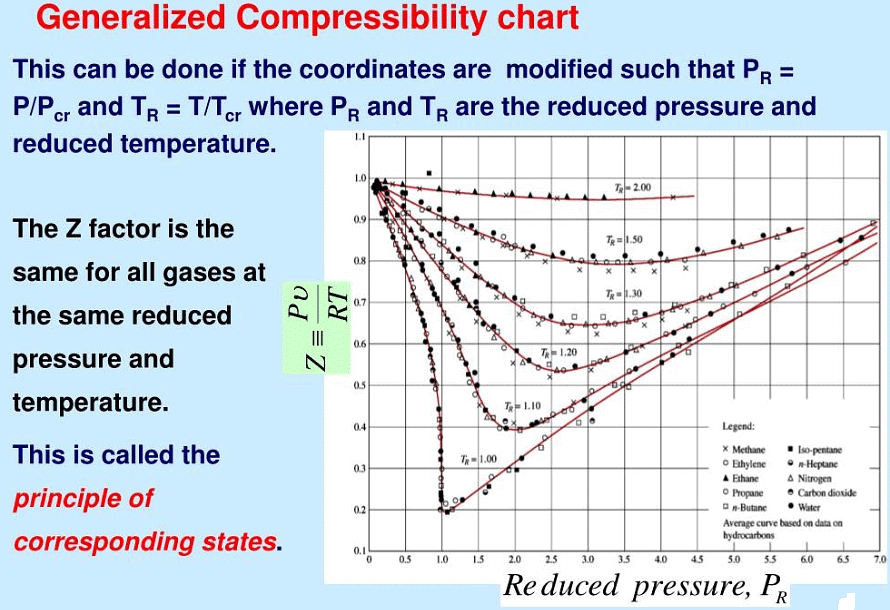
According to van der Waals, the theorem of corresponding states, it tells that all fluids, when compared at the same reduced temperature and reduced pressure, have approximately the same compressibility factor and all deviate from ideal gas behaviour to about the same degree.

Van der Waals equation

The Van der Waals equation is an equation of state that describes the behavior of real gases by accounting for the finite size of molecules and the intermolecular forces (attractive and repulsive) between them. It is a modification of the Ideal Gas Law to provide a more accurate description of real gases, especially under conditions of high pressure and low temperature, where ideal gas behavior breaks down.

The Van der Waals equation is given by:$\backslash left(\; P\; +\; \backslash frac\{a\}\{V^2\}\; \backslash right)(V\; -\; b)\; =\; RT$

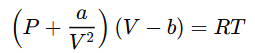
Where:

• P = Pressure of the gas
• V = Volume of the gas
• T = Temperature of the gas
• R = Universal gas constant
• a = Van der Waals constant for intermolecular attraction (affects the attractive forces between molecules)
• b = Van der Waals constant for molecular volume (affects the finite size of molecules)

Explanation of the Terms:

1. P+ a/V²: This term accounts for the attractive forces between gas molecules. In real gases, molecules attract each other, which reduces the pressure exerted by the gas on the container walls. The term $\frac{a}{V}\backslash frac\{a\}\{V^2\}$V2a adjusts for the intermolecular attraction (where "a" is a constant specific to the gas).

2. (V−b): This term corrects for the volume occupied by gas molecules. In the Ideal Gas Law, gas molecules are considered point masses, but real molecules have finite size and occupy a certain volume. The volume term $bb$b accounts for the effective volume occupied by the molecules themselves (where "b" is a constant specific to the gas).

$RT$3. RT: This represents the ideal gas contribution, where the gas behaves ideally and obeys the Ideal Gas Law.

Modifications in the Van der Waals Equation:

• Volume Occupied by Molecules:
  To account for the volume that gas molecules themselves occupy, the molar volume $VmV\_m$Vm is adjusted by subtracting $bb$b, the volume occupied by one mole of gas molecules. This modification gives: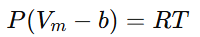
• Intermolecular Interactions:
  Real gas molecules interact with each other (attractive forces at low pressure, repulsive forces at high pressure), causing deviations from ideal behavior. To account for this, a term involving the constant $aa$a is added to the pressure: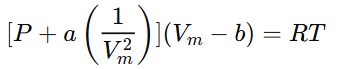

This leads to the general form of the Van der Waals equation for real gases: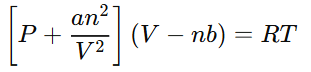

Ideal Gas Behavior:

When the molar volume V_m is large, the term b becomes negligible, and the intermolecular forces term a/V_m² becomes insignificant compared to the pressure. In such conditions, the Van der Waals equation simplifies to the Ideal Gas Law:

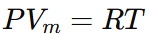
Thus, the Van der Waals equation provides a more accurate description of real gases by correcting for the finite size of molecules and their intermolecular interactions, while the Ideal Gas Law holds for gases that behave nearly ideally under conditions of low pressure and high temperature.

Theorem of corresponding states

The principle of Corresponding States (PCS) was stated by van der Waals and reads: “Substances behave alike at the same reduced states. Substances at same reduced states are at corresponding states.” That is,

“Substances at corresponding states behave alike.”

Reduced properties are used to define corresponding states. Reduced properties provide a measure of the “departure” of the conditions of the substance from its own critical conditions and are defined as follows:

• P_c = Critical pressure
• T_c = Critical temperature
• $V\_c$V_c = Critical volume 
  We introduce reduced variables to express the equation in a form that is independent of the specific gas. The reduced variables are defined as: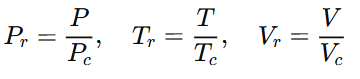

If Pr = Tr = vr = 1, the substance is at its critical condition. If we are beyond critical conditions, Tr > 1, Pr > 1 and vr > 1. By the same token, if all the conditions are subcritical, Tr < 1, Pr < 1 and vr < 1. Critical conditions become the scaling factor by which substances can be compared among each other in terms of their “departure from criticality” or reduced properties.

The PCS says that all gases behave alike at the same reduced conditions. That is, if two gases have the same “relative departure” from criticality (i.e., they are at the same reduced conditions), the corresponding state principle demands that they behave alike. In this case, the two conditions “correspond” to one another, and we are to expect those gases to have the same properties.

The Corresponding State Principle can be derived from vdW EOS. If we recall,

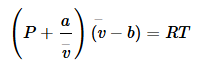
By substitution into the van der Waals equation we find: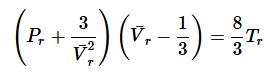 

Compressibility factor at the critical point

The compressibility factor (Z) is a measure of how much a real gas deviates from ideal gas behavior. It is defined as: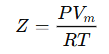Where:

• $P$P = Pressure
• $\mathrm{<span\; style="background-color:\; transparent;\; word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">Vm\; =\; Molar\; volume\; of\; the\; gas</span>}$
• R = Universal gas constant
• T = Temperature

For ideal gases, the compressibility factor Z is always equal to 1. However, for real gases, Z varies depending on the conditions of pressure, temperature, and the specific gas.

At the Critical Point:

The critical point refers to the temperature and pressure at which the liquid and gas phases of a substance become indistinguishable. It is characterized by:

• Critical temperature (T_c): The highest temperature at which a gas can be liquefied, no matter the pressure.
• Critical pressure (P_c): The pressure required to liquefy a gas at the critical temperature.
• Critical volume ($V\_c$V_c): The molar volume of the substance at the critical temperature and pressure.

At the critical point, the compressibility factor (Z) of a real gas is typically found to be close to 0.3 to 0.4, depending on the substance. This value is less than 1, indicating that the gas is more compressible than an ideal gas under the same conditions.