Exponent Rules | Mathematics for Digital SAT PDF Download

Exponent rules are those laws that are used for simplifying expressions with exponents. Many arithmetic operations like addition, subtraction, multiplication, and division can be conveniently performed in quick steps using the laws of exponents. These rules also help in simplifying numbers with complex powers involving fractions, decimals, and roots.

What are Exponent Rules?

Exponent rules, which are also known as the 'laws of exponents' or the 'properties of exponents' make the process of simplifying expressions involving exponents easier. These rules are helpful to simplify the expressions that have decimals, fractions, irrational numbers, and negative integers as their exponents.
For example, if we need to solve 3⁴ × 3², we can easily do it using one of the exponent rules which says, a^m × aⁿ = a^{m + n}. Using this rule, we will just add the exponents to get the answer, while the base remains the same, that is, 3⁴ × 3² = 3^{4 + 2} = 3⁶. Similarly, expressions with higher values of exponents can be conveniently solved with the help of the exponent rules. Here is the list of exponent rules.

• a⁰ = 1
• a¹ = a
• a^m × aⁿ = a^m+n
• a^m / aⁿ = a^m−n
• a^−m = 1/a^m
• (a^m)ⁿ = a^mn
• (ab)^m = a^mb^m
• (a/b)^m = a^m/b^m

Laws of Exponents

The different rules of exponents are also known as the laws of exponents (or) properties of exponents. The laws of exponents were already mentioned in the previous section. Most of them have specific names such as the product rule of exponents, the quotient rule of exponents, the zero rule of exponents, the negative rule of exponents, etc.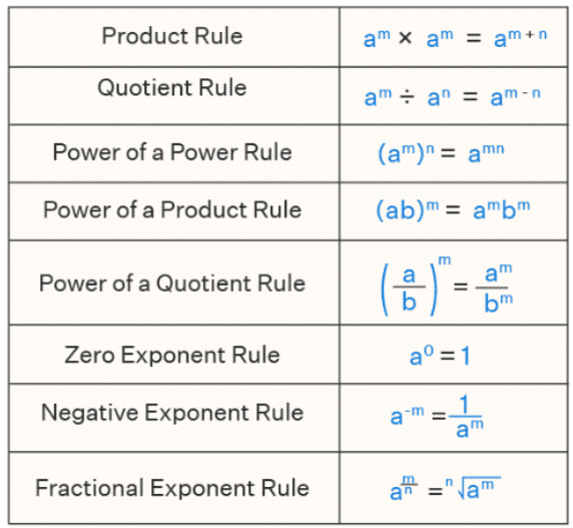

Product Law of Exponents

The product rule of exponents is used to multiply expressions with the same bases. This rule says, "To multiply two expressions with the same base, add the exponents while keeping the base the same." This rule involves adding exponents with the same base. Here the rule is useful to simplify two expressions with a multiplication operation between them.
a^m × aⁿ = a^m+n
Observe the following example.

This shows that without using the law, the expression involves more calculation.

Quotient Law of Exponents

The quotient law of exponents is used to divide expressions with the same bases. This rule says, "To divide two expressions with the same base, subtract the exponents while keeping the base same." This is helpful in solving an expression, without actually performing the division process. The only condition that is required is that the two expressions should have the same base.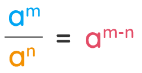

Here is an example.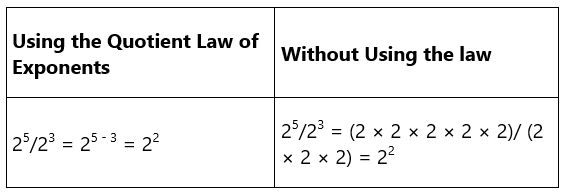

We can clearly see that without using the law, the expression involves more calculation.

Zero Law of Exponents

The zero law of exponents is applied when the exponent of an expression is 0. This rule says, "Any number (other than 0) raised to 0 is 1." Note that 0⁰ is not defined, it is an indeterminate form. This will help us understand that irrespective of the base the value for a zero exponent is always equal to 1.
a⁰ = 1
Here is an example.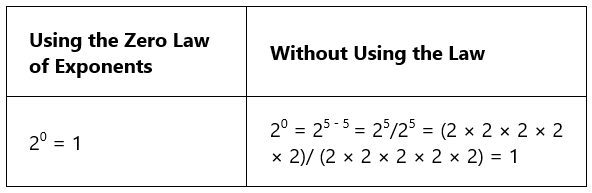

Using the law we simply get 2⁰ = 1. Alternatively, without using the law we can understand the same law with more number of steps.

Negative Law of Exponents

The negative law of exponents is used when an exponent is a negative number. This rule says, "To convert any negative exponent into positive exponent, the reciprocal should be taken." The expression is transferred from the numerator to the denominator with the change in sign of the exponent values.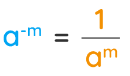

Here is an example.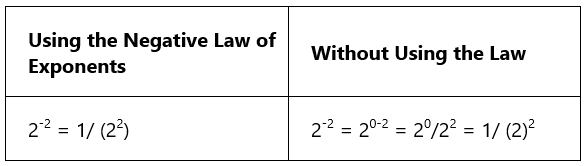

Using the law, we can solve it in just one go, like 2^-2 = 1/(2²). Alternatively, without using the law the process is lengthy.

Power of a Power Law of Exponents

The 'power of a power law of exponents' is used to simplify expressions of the form (a^m)ⁿ. This rule says, "When we have a single base with two exponents, just multiply the exponents." The two exponents are available one over the other. These can be conveniently multiplied to make a single exponent.
(a^m)ⁿ = a^mn
Here is an example.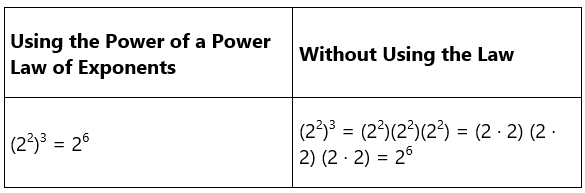

Using this law reduces the process of calculation.

Power of Product Rule of Exponents

The 'power of a product rule of exponents' is used to find the result of a product that is raised to an exponent. This law says, "Distribute the exponent to each multiplicand of the product."
(ab)^m = a^mb^m

Here is an example.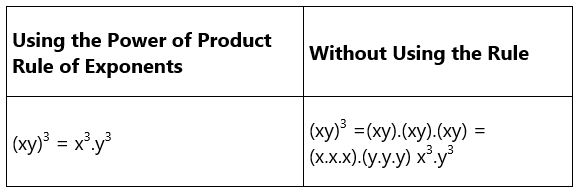 

Using the law, (xy)³ = x³.y³. On the other hand, the same thing can be expressed in multiple steps, without using the law. (xy)³ =(xy).(xy).(xy) = (x.x.x).(y.y.y) x³.y³ 

Power of a Quotient Rule of Exponents 

The power of a quotient rule of exponents is used to find the result of a quotient that is raised to an exponent. This law says, "Distribute the exponent to both the numerator and the denominator." Here, the bases are different and the exponents are the same for both the bases.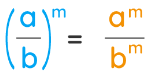

Here is an example of the exponent rule given above.

We can use the law and simply solve, and we can also solve the same expression without the law which involves multiple steps.

Fractional Exponents Rule

The fractional exponents rule says, a^1/n = ⁿ√a. i.e., When we have a fractional exponent, it results in radicals. For example, a^1/2 = √a, a^1/3 = ∛a, etc. This rule is further extended for complex fractional exponents like am/n. Using the power of a power rule of exponents (that we have studied in one of the previous sections),
a^m/n = (a^m)^1/n
Now, by using the fractional exponents rule, this fractional power turns into a radical.
a^m/n = ⁿ√(a^m)
This is also used as an alternate form of the fractional exponents rule. Thus, this rule is defined in two ways:

• a^1/n = ⁿ√a
• a^m/n = ⁿ√(a^m)

Exponent Rules Chart

The rules of exponents explained above can be summarized in a chart as shown below.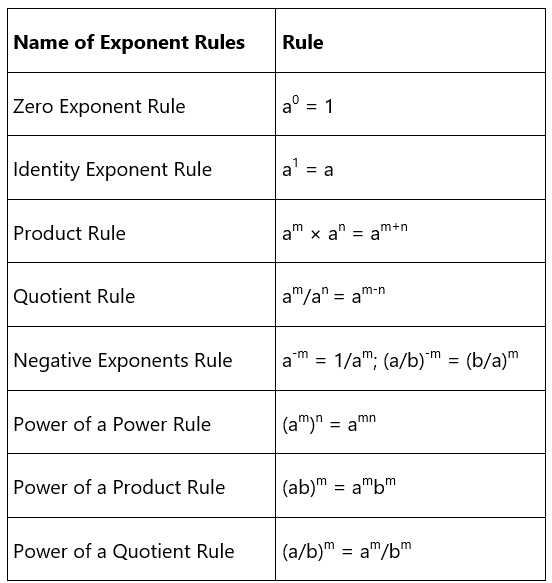

Exponent Rules Examples

Example: Simplify the expression by using the laws of exponents: 10^-3 × 10⁴
Solution: According to the exponent rules, to multiply two expressions with the same base, we add the exponents while the base remains the same.
This means, 10^-3 × 10⁴ = 10^{(-3 + 4)} = 10¹ = 10