Mutually Exclusive Events | Mathematics for Digital SAT PDF Download

When you toss a coin, you either get heads or tails, but there is no other way you could get both results. This is an example of mutually exclusive events. In probability theory, two events are said to be mutually exclusive events if they cannot occur at the same time or simultaneously. In other words, mutually exclusive events are called disjoint events.
Further, if two events are considered disjoint events, then the probability of both events occurring at the same time will be zero.

What Are Mutually Exclusive Events?

What is the meaning of mutually exclusive events? Mutually exclusive events are the events that cannot occur or happen at the same time. In other words, the probability of the events happening at the same time is zero.
Example of Mutually Exclusive Events
A student wants to go to school. There are two paths; one that takes him to school and the other one that takes him home. Which path will he choose? He will choose one of the two paths. Obviously, he can't choose both at the same time. This is an example of a mutually exclusive events.

How Do You Calculate Mutually Exclusive Events?

Mutually exclusive events are events that cannot occur or happen at the same time. The occurrence of mutually exclusive events at the same time is 0. If A and B are two mutually exclusive events in math, the probability of them both happening together is: P(A and B) = 0. The formula for calculating the probability of two mutually exclusive events is given below:
P(A or B) =  P(A) + P(B)
Do you know special symbols are used to show the relation between two sets: The two important relationships between two sets are the intersection of sets and union of sets.

• Intersection of sets: The symbol used for the intersection is "∩" and "and" is also used. If two sets are there say for example; A = {1, 2, 3} and B = {2, 3, 4}. Then A intersection B is represented as A∩B.
  A ∩ B = {2, 3}
• Union of sets: The symbol used for the union is "∪" and "or" is also used. If two sets are there say for example; A = {1, 2, 3} and B = {2, 3, 4}. Then A union B is represented as A∪B.
  A ∪ B = {1, 2, 3, 4}

Probability of Disjoint (or) Mutually Exclusive Events

The probability of disjoint or mutually exclusive events A and B is written as the probability of the intersection of the events A and B. Probability of Disjoint (or) Mutually Exclusive Events = P ( A ∩ B) = 0. In probability, the specific addition rule is valid when two events are mutually exclusive events. It states that the probability of either event occurring is the sum of probabilities of each event occurring. If A and B are said to be mutually exclusive events then the probability of an event A occurring or the probability of event B occurring is given as P(A) + P(B),
P (A U B) = P(A) + P(B)

Some of the examples of the mutually exclusive events are:

• When tossing a coin, the event of getting head and tail are mutually exclusive events. Because the probability of getting head and tail simultaneously is 0.
• In a six-sided die, the events “2” and “5” are mutually exclusive events. We cannot get both events 2 and 5 at the same time when we threw one die.
• In a deck of 52 cards, drawing a red card and drawing a club are mutually exclusive events because all the clubs are black.

If the events A and B are not mutually exclusive events, the probability of getting A or B is given as:
P (A U B) = P(A) + P(B) – P (A ∩ B)

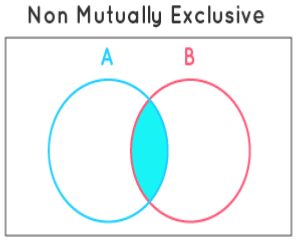
How Do You Show Mutually Exclusive Events?

We can use Venn diagrams to show mutually exclusive events. The figures shown below indicate mutually exclusive events and events that are not mutually exclusive events or non-mutually exclusive events. Note that there is no common element in mutually exclusive events.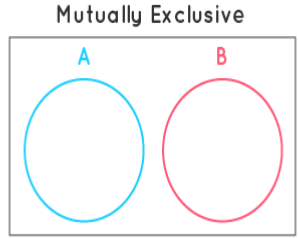

Do Mutually Exclusive Events Add up to 1?

We know that mutually exclusive events cannot occur at the same time. The sum of the probability of mutually exclusive events can never be greater than 1 It is always less than 1, until and unless the same set of events are also exhaustive (at least one of them being true). In this case, the sum of their probability is exactly 1.

Mutually Exclusive Events Probability Rules

In probability theory, two events are mutually exclusive events or disjoint if they do not occur at the same time. A clear case is the set of results of a single coin toss, which can end in either heads or tails, but not for both. While tossing the coin, both outcomes are collectively exhaustive, which suggests that at least one of the consequences must happen, so these two events collectively exhaust all the possibilities.
Though, not all mutually exclusive events are commonly exhaustive. For example, the outcomes of 1 and 4 on rolling six-sided dice, are mutually exclusive events (both 1 and 4 cannot come as result at the same time) but are not collectively exhaustive (it can result in distinct outcomes such as 2,3,5,6). Further, from the definition of mutually exclusive events, the following rules for probability can be concluded.

• Addition Rule: P (A + B) = 1
• Subtraction Rule: P (A U B)’ = 0
• Multiplication Rule: P (A ∩ B) = 0

There are different varieties of events also. For instance, think of a coin that has a Head on both sides of the coin or a Tail on both sides. It doesn’t matter how many times you flip it, it will always occur Head (for the first coin) and Tail (for the second coin). If we check the sample space of such an experiment, it will be either {H} for the first coin and {T} for the second one. Such events have single point in the sample space and are called  “Simple Events”. Such kind of two sample events is always mutually exclusive events.

Conditional Probability for Mutually Exclusive Events

Conditional probability is stated as the probability of event A, given that another event B has occurred. For two independent events A and B, the conditional probability of event B given that  A has occurred is denoted by the expression P( B|A) and it is defined using the following equation.

P(B|A)= P (A ∩ B)/P(A)

Let us redefine the above equation using multiplication rule: P (A ∩ B) = 0

P(B|A)= 0/P(A)

So the conditional probability formula for mutually exclusive events is:

P (B | A) = 0