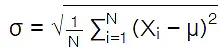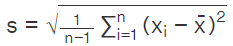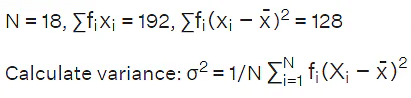Standard Deviation | The Complete SAT Course - Class 10 PDF Download
What is Standard Deviation?
- Standard deviation is the degree of dispersion or the scatter of the data points relative to its mean, in descriptive statistics. It tells how the values are spread across the data sample and it is the measure of the variation of the data points from the mean. The standard deviation of a sample, statistical population, random variable, data set, or probability distribution is the square root of its variance.
- When we have n number of observations and the observations are x1, x2,.....xn, then the mean deviation of the value from the mean is determined as
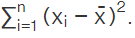 However, the sum of squares of deviations from the mean doesn't seem to be a proper measure of dispersion. If the average of the squared differences from the mean is small, it indicates that the observations xi are close to the mean
However, the sum of squares of deviations from the mean doesn't seem to be a proper measure of dispersion. If the average of the squared differences from the mean is small, it indicates that the observations xi are close to the mean This is a lower degree of dispersion. If this sum is large, it indicates that there is a higher degree of dispersion of the observations from the mean
This is a lower degree of dispersion. If this sum is large, it indicates that there is a higher degree of dispersion of the observations from the mean 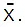 Thus we conclude that
Thus we conclude that 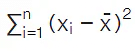 is a reasonable indicator of the degree of dispersion or scatter.
is a reasonable indicator of the degree of dispersion or scatter. We take
We take 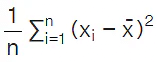 as a proper measure of dispersion and this is called the variance(σ2). The square root of the variance is the standard deviation.
as a proper measure of dispersion and this is called the variance(σ2). The square root of the variance is the standard deviation.
Steps to Calculate Standard Deviation
- Find the mean, which is the arithmetic mean of the observations.
- Find the squared differences from the mean. (The data value - mean)2
- Find the average of the squared differences. (Variance = The sum of squared differences ÷ the number of observations)
- Find the square root of variance. (Standard deviation = √Variance)
Standard Deviation Formula
- The spread of statistical data is measured by the standard deviation. The degree of dispersion is computed by the method of estimating the deviation of data points. You can read about dispersion in summary statistics. As discussed, the variance of the data set is the average square distance between the mean value and each data value.
- And standard deviation defines the spread of data values around the mean. Here are two standard deviation formulas that are used to find the standard deviation of sample data and the standard deviation of the given population.

Formula for Calculating Standard Deviation
The population standard deviation formula is given as:
Here,
- σ = Population standard deviation
- μ = Assumed mean
Similarly, the sample standard deviation formula is:
Here,
- s = Sample standard deviation
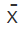 = Arithmetic mean of the observations
= Arithmetic mean of the observations
Standard Deviation of Ungrouped Data
The calculations for standard deviation differ for different data. Distribution measures the deviation of data from its mean or average position. There are two methods to find the standard deviation.
- actual mean method
- assumed mean method
Standard Deviation by The Actual Mean Method
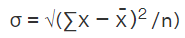
- Consider the data observations 3, 2, 5, 6. Here the mean of these data points is 16/4 = 4.
- The squared differences from mean = (4-3)2 + (2-4)2 + (5-4)2 + (6-4)2 = 10
- Variance = Squared differences from mean/ number of data points =10/4 =2.5
- Standard deviation = √2.5 = 1.58
Standard deviation by Assumed Mean Method
- When the x values are large, an arbitrary value (A) is chosen as the mean. The deviation from this assumed mean is calculated as d = x - A.
σ = √[(∑(d)2 /n) - (∑d/n)2]
Standard Deviation of Grouped Data
- When the data points are grouped, we first construct a frequency distribution.
Standard Deviation of Grouped Discrete Frequency Distribution
For n number of observtions, x1,x2,....xn, and the frequency,
f1, f2, f3, . . . fn the standard deviation is: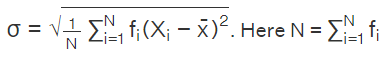
Example: Let's calculate the standard deviation for the data given below:
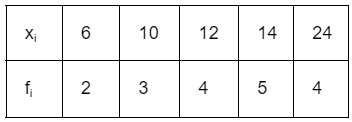
Calculate mean (
): (6+8 +10+12+ 14)/5 = 10
= 1/18 × 128 = 7.1
Calculate SD: σ = √Variance = √ 7.1 = 2.66
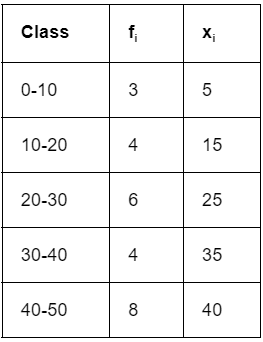
Standard Deviation of Grouped Continuous Frequency Distribution
- If the frequency distribution is continuous, each class is replaced by its midpoint. Then the Standard deviation is calculated by the same technique as in discrete frequency distribution. Consider the following example. xi is calculated as the midpoint of each class. Then the same standard deviation formula is applied.
Standard Deviation of Random Variables
- The measure of spread for the probability distribution of a random variable determines the degree to which the values differ from the expected value. This is a function that assigns a numerical value to each outcome in a sample space. This is denoted by X, Y, or Z, as it is a function.
- If X is a random variable, the standard deviation is determined by taking the square root of the sum of the product of the squared difference between the random variable, x, and the expected value (𝜇) and the probability associated value of the random variable.
- The standard deviation of the probability distribution of X, 𝜎 =
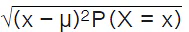
This is also equivalent to 𝜎 =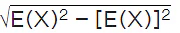
Standard Deviation of Probability Distribution
The experimental probability consists of many trials. When the difference between the theoretical probability of an event and its relative frequency get closer to each other, we tend to know the average outcome. This mean is known as the expected value of the experiment denoted by 𝜇.
- In a normal distribution, the mean is zero and the standard deviation is 1.
- In a binomial experiment, the number of successes is a random variable. If a random variable has a binomial distribution, its standard deviation is given by: 𝜎= √npq, where mean: 𝜇 = np, n = number of trials, p = probability of success and 1-p =q is the probability of failure.
- In a Poisson distribution, the standard deviation is given by 𝜎= √λt, where λ is the average number of successes in an interval of time t.
Standard Deviation Tips:
- For n as the sample or the population size, the square root of the average of the squared differences of data observations from the mean is called the standard deviation.
- Standard deviation is the positive square root of variance.
- Standard deviation is the indicator that shows the dispersion of the data points about the mean.
|
433 videos|220 docs|166 tests
|