What are Quadratic Polynomials? | The Complete SAT Course - Class 10 PDF Download
Introduction
- Quadratic polynomial is a polynomial in which the highest degree monomial is of the second degree. A quadratic polynomial is also known as a second-order polynomial. This means that at least one of the variables should be raised to the power of two while the other variable powers will be lesser than or equal to two but greater than -1.
- A quadratic polynomial can have multiple variables. However, a univariate quadratic polynomial that has a single variable is the most commonly used polynomial. The graph of a univariate quadratic polynomial is a parabola.
What is Quadratic Polynomial?
- A quadratic polynomial is one in which the highest power of a variable term in the polynomial expression is equal to 2. To check the degree of a polynomial only the exponent of the variable is considered. The power of a coefficient or a constant term is not taken into account. When a quadratic polynomial is equated to 0 it gives rise to a quadratic equation or a quadratic function. The solutions of such an equation are known as the roots or the zeros of the quadratic equation.
Quadratic Polynomial Definition
- A quadratic polynomial is a second-degree polynomial where the value of the highest degree term is equal to 2. The general form of a quadratic equation is given as ax2 + bx + c = 0. Here, a and b are coefficients, x is the unknown variable and c is the constant term. As this equation contains a quadratic polynomial, hence, solving it will give two solutions. This implies that there can be two values of x.
Quadratic Polynomial Example
Suppose we have a quadratic polynomial x2 + 4x + 4 = 0. Then to find the solutions of this equation we factorize it as (x + 2)(x + 2) = 0. Thus, the roots of this quadratic equation will be x = -2, -2.
Quadratic Polynomial Formula
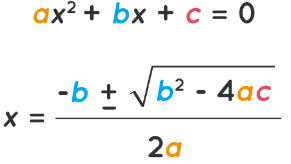
- The general formula of a single variable quadratic polynomial is given as ax2 + bx + c. When this quadratic polynomial is used in an equation it is expressed as ax2 + bx + c = 0. There are many methods that can be used to find the solutions of an equation containing a quadratic polynomial. These methods are factorizing a quadratic equation, completing the squares, using graphs, and using the quadratic polynomial formula. Out of all these techniques, the simplest way to find the roots of a quadratic polynomial is by using the formula. An added benefit of this method is that several important conclusions can be made by analyzing the discriminant. The quadratic polynomial formula is given below:
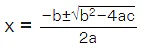
- The two values of x that are obtained after applying this formula are known as the solutions, the zeros or the roots of the quadratic equation.
- The value b2 - 4ac is called the discriminant. It is denoted by D. The nature of the roots can be determined by using the discriminant.
Quadratic Polynomial Roots

- The method of factorization is only applicable to certain quadratic polynomials. However, the quadratic polynomial formula can be used for any type of quadratic equation. Furthermore, the value of the discriminant can be used to analyze the nature of the roots of a quadratic polynomial. Given below are the various conditions that can help to predict the nature of the roots:
- D > 0: If the discriminant is positive, it indicates that the roots are real and distinct.
- D = 0: If the value of the discriminant is equal to zero, then both the roots are real and are equal to each other.
- D < 0: Both the roots are imaginary numbers if the discriminant is negative.
Quadratic Polynomial Sum and Product of Roots
- Using the roots of the equation containing the quadratic polynomial, a relationship can be established between the roots and the coefficients. The sum and the product of the roots of a quadratic polynomial can be determined using the coefficients and the constant term. Suppose one root is given by α and the other root is given by β. For a quadratic equation, ax2 + bx + c = 0, containing a quadratic polynomial, the formula for the sum and product of roots is given below:
- Sum of roots: α + β = - Coefficient of x / Coefficient of x2 = - b / a
- Product of roots: α . β = Constant / Coefficient of x2 = c / a
- If the sum and product of the roots has been specified then the original quadratic polynomial can be obtained. This is given by
x2 - ( α + β )x + α . β = 0 - This can also be used to factor qudartic polynomials.
Quadratic Polynomial Graph
- The graph of a quadratic polynomial in a single variable is given by a parabola. If the quadratic polynomial is denoted as ax2 + bx + c, then the equation of the parabola is y = ax2 + bx + c. To obtain the quadratic polynomial graph, test points can be determined by substituting the value of x in the aforementioned equation and getting the corresponding values of y. The two points where the parabola cuts the x-axis are the solutions of the quadratic equation. Furthermore, their values will be equal to the roots, α and β.
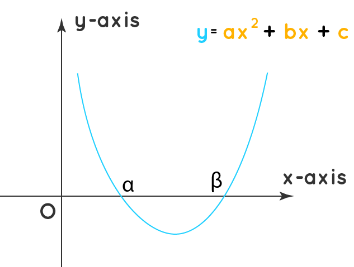
How to Find Quadratic Polynomial?
- A quadratic polynomial can be obtained by using the zeros or roots of the equation. Suppose the two roots are given as -4 and 2. The steps to find the quadratic polynomial are as follows:
- Step 1: Find the sum of the two roots. Sum of roots = -4 + 2 = -2.
- Step 2: Find the product of the two roots. Product of roots = -4 * 2 = -8
- Step 3: Substitute these values in the expression x2 - (sum of the roots)x + (product of the roots). Thus, the quadratic polynomial is x2 + 2x - 8
How to Factorize Quadratic Polynomials?
- Generally, factorization can be considered as the reverse of multiplying two expressions. Few methods for factorization of quadratic polynomials are listed below:
Common Factor Method
- In this method, we have to look at all the terms and determine the common terms.
- If there is a common term in the equation, we will factor it out for the polynomial.
- We use distributive law in reverse.
x(a+b) = xa + xb - We notice that each term has an 'x' in the equation and the common factor is taken out using the distributive law in reverse as follows,
xa + xb = x(a + b)
Example: What are the common factors of the terms in the quadratic polynomial equation 8x2 − 4x = 0?
Let's apply the distributive law in reverse.
4x is a common factor in the equation.
Thus, 4x(2x - 1) are the factors of 8x2 − 4x = 0
Sum of Difference Method
- The sum and the difference of two terms are most likely used when the two factors match exactly, except one term involves addition and the other is a difference.
For example: (a + b)(a - b) - When we expand and multiply these terms, we get a × a + ab - ab - b × b
- Like terms will be in the middle and will result in zero, thus leaving behind a2 and -b2
- Thus, the formula becomes (a + b)(a - b) = a2 - b2
Example: Find the solution of (5 + x)(5 - x) using the sum of the difference method.
Apply the sum of the difference method for solving the terms.
(a + b)(a - b) = a2 - b2
(5 + x)(5 - x) = (52 - x2) = 25 - x2
Factor By Grouping Method
- Factor by grouping means that we have to group all the terms with common factors before factoring.
- The following steps are used in the factor by grouping method.
- From the given quadratic polynomial, take out a factor from each group.
- Factorize each group of the expression.
- Now take out the factor common to the group formed.
Example: How can you factorize the quadratic polynomial a2 - ac + ab - bc by the grouping method?
a2 - ac + ab - bc
Take the common factor from the quadratic polynomial.
= a(a - c) + b(a - c)
= (a - c) (a + b)
Thus, by factoring expressions we get (a - c) (a + b).
Perfect Square Trinomials Method
- The method of converting any quadratic polynomial into a perfect square is known as the perfect square trinomial method.
- The following equations are the perfect square trinomial formulas:
a2 + 2ab + b2 = (a + b)2
a2 - 2ab + b2 = (a - b)2
Example: Is the given quadratic polynomial x2 – 8x + 16 a perfect square?
On using the formula, we get
x2 – 8x + 16 = x2 – 2(1)(4)x + 42
= (x - 4)2
Thus, the given quadratic polynomial is a perfect square.
Important Notes on Quadratic Polynomial
- A quadratic polynomial is a polynomial where the degree is equal to two.
- A quadratic polynomial can have 2 roots.
- The roots of a quadratic equation can be determined by using the formula

- The discriminant, equal to b2 - 4ac, is used to check the nature of the roots.
- The sum and product of the roots can be substituted in the expression, x2 - (sum of roots)x + (product of the roots), to get the quadratic polynomial.
- The graph of a quadratic polynomial is a parabola.
|
433 videos|220 docs|166 tests
|
















