Vertex of a Parabola | Mathematics for Grade 12 PDF Download

Introduction

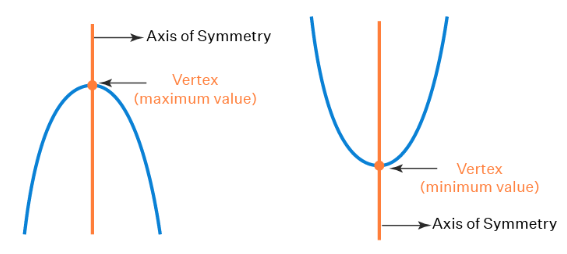
• The vertex of a parabola is a point at which the parabola makes its sharpest turn. A parabolic function has either a maximum value (if it is of the shape '∩') or a minimum value (if it is of the shape 'U"). The vertex of a parabola is also the point of intersection of the parabola and its axis of symmetry.
  

Vertex of a parabola

Different Types of Parabolas

• There can be two types of equations of a parabola which represent 4 different types of parabolas. The equation of any parabola involves a quadratic polynomial.

Top/Bottom Opened Parabolas:

• The equation of a top/bottom opened parabola can be in one of the following three forms:
  • Standard form: y = ax² + bx + c
  • Vertex Form: y = a (x - h)² + k
  • Intercept Form: y = a (x - p)(x - q)
• In each of the cases, the parabola opens up if a > 0, and it opens down if a < 0.

Left/Right Opened Parabolas:

• The equation of a left/right opened parabola can be in one of the following three forms:
  • Standard form: x = ay² + by + c
  • Vertex Form: x = a (y - k)² + h
  • Intercept Form: x = a (y - p)(y - q)
• In each of the cases, the parabola opens to the right side if a > 0, and it opens to the left side if a < 0.

Vertex of a Parabola Formula

Here are the formulas to find the vertex of any type of parabola when it is in different forms.

Finding Vertex of a Parabola From Standard Form

• We know that the equation of a parabola in standard form can be either of the form y = ax² + bx + c (up/down) or of the form x = ay² + by + c (left/right). Let us see the steps to find the vertex of the parabola in each case.

Vertex of a Top/Bottom Opened Parabola

• When a parabola opens up or down, its equation in the standard form is of the form y = ax² + bx + c. Here are the steps to find the vertex (h, k) of such parabolas. The steps are explained with an example where we will find the vertex of the parabola y = 2x² - 4x + 1.
  • Step - 1: Compare the equation of the parabola with the standard form y = ax² + bx + c.
    By comparing y = 2x² - 4x + 1 with the above equation, a = 2, b = -4, and c = 1.
  • Step - 2: Find the x-coordinate of the vertex using the formula, h = -b/2a
    Then we get h = -(-4) / (2 × 2) = 1.
  • Step - 3: To find the y-coordinate (k) of the vertex, substitute x = h in the expression ax² + bx + c.
    Then k = 2(1)² - 4(1) + 1 = 2 - 4 + 1 = -1.
  • Step - 4: Write the vertex (h, k) as an ordered pair.
    The vertex = (h, k) = (1, -1).

Vertex of a Left/RightOpened Parabola

• When a parabola opens left or right, its equation in the standard form is of the form x = ay² + by + c. Here are the steps to find the vertex (h, k) of such parabolas which are explained with an example where we will find the vertex of the parabola x = 2y² - 4y + 1.
  • Step - 1: Compare the equation of the parabola with the standard form x = ay² + by + c.
    By comparing x = 2y² - 4y + 1 with the above equation, a = 2, b = -4, and c = 1.
  • Step - 2: Find the y-coordinate of the vertex using the formula, k = -b/2a
    Then we get k = -(-4) / (2 × 2) = 1.
  • Step - 3: To find the x-coordinate (h) of the vertex, substitute y = k in the expression ay² + by + c.
    Then h = 2(1)² - 4(1) + 1 = 2 - 4 + 1 = -1.
  • Step - 4: Write the vertex (h, k) as an ordered pair.
    The vertex = (h, k) = (-1, 1).

Finding Vertex of a Parabola From Vertex Form

• We know that the equation of a parabola in vertex form can be either of the form y = a(x - h)² + k (up/down) or of the form x = a(y - k)² + h (left/right).

Vertex of a Top/Bottom Opened Parabola

• When a parabola opens to the top or bottom, its equation in the vertex form is of the form y = a(x - h)² + k. Here are the steps to find the vertex (h, k) of such parabolas. The steps are explained with an example where we will find the vertex of the parabola y = 2(x + 3)² + 5
  • Step - 1: Compare the equation of the parabola with the vertex form y = a(x - h)² + k and identify the values of h and k.
    By comparing y = 2(x + 3)² + 5 with the above equation, h = -3 and k = 5.
  • Step - 2: Write the vertex (h, k) as an ordered pair.
    The vertex = (h, k) = (-3, 5).

Vertex of a Left/RightOpened Parabola

• When a parabola opens to the left or to the right side, its equation in the vertex form is of the form x = a(y - k)² + h. Here are the steps to find the vertex (h, k) of such parabolas. The steps are explained with an example where we will find the vertex of the parabola x = 2(y + 3)² + 5
  • Step - 1: Compare the equation of the parabola with the vertex form x = a(y - k)² + h and identify the values of h and k.
    By comparing x = 2(y + 3)² + 5 with the above equation, h = 5 and k = -3.
  • Step - 2: Write the vertex (h, k) as an ordered pair.
    The vertex = (h, k) = (5, -3).

Finding Vertex of a Parabola From Intercept Form

• We know that the equation of a parabola in intercept form can be either of the form y = a (x - p) (x - q) (up/down) or of the form y = a(y - p)(y - q) (left/right). 

Vertex of a Top/Bottom Opened Parabola

• When a parabola opens to the top or bottom, its equation in the intercept form is of the form y = a (x - p) (x - q), where (p, 0) and (q, 0) are the x-intercepts of the parabola. Here are the steps to find the vertex (h, k) of such parabolas. The steps are explained with an example where we will find the vertex of the parabola y = -(x + 3) (x - 7)
  • Step - 1: Compare the equation of the parabola with the intercept form y = a (x - p) (x - q) and identify the values of p and q.
    By comparing y = -(x + 3) (x - 7) with the above equation, p = -3 and q = 7.
  • Step - 2: Find the x-coordinate of the vertex, h using the formula h = (p + q)/2.
    Then h = (-3 + 7)/2 = 4/2 = 2.
  • Step - 3: Find the y-coordinate of the vertex, k by substituting x = h in the expression a (x - p) (x - q).
    Then k = -(2 + 3) (2 - 7) = 25.
  • Step - 4: Write the vertex (h, k) as an ordered pair.
    The vertex = (h, k) = (2, 25).

Vertex of a Left/Right Opened Parabola

• When a parabola opens to the left or right side, its equation in the intercept form is of the form x = a (y - p) (y - q), where (0, p) and (0, q) are the y-intercepts of the parabola. Here are the steps to find the vertex (h, k) of such parabolas. The steps are explained with an example where we will find the vertex of the parabola x = -(y + 3) (y - 7)
• Step - 1: Compare the equation of the parabola with the intercept form x = a (y - p) (y - q) and identify the values of p and q.
  By comparing x = -(y + 3) (y - 7) with the above equation, p = -3 and q = 7.
• Step - 2: Find the y-coordinate of the vertex, k using the formula k = (p + q)/2.
  Then k = (-3 + 7)/2 = 4/2 = 2.
• Step - 3: Find the x-coordinate of the vertex, h by substituting y = k in the expression a (y - p) (y - q).
  Then h = -(2 + 3) (2 - 7) = 25.
• Step - 4: Write the vertex (h, k) as an ordered pair.
  The vertex = (h, k) = (25, 2).

Properties of Vertex of a Parabola

Here are some properties of the vertex of a parabola that follow from the definition of the vertex of a parabola.

• The vertex of a parabola is its turning point.
• Since the vertex of a parabola is its sharp turning point, the derivative of the function representing the parabola at the vertex is 0.
• A top/bottom open parabola either has a maximum or a minimum at its vertex.
• The vertex of a left or right open parabola is neither a maximum nor a minimum to it.
• Any type of parabola intersects its axis of symmetry at its vertex.

Important Notes Related to Vertex of a Parabola:

• The vertex of a parabola f(x) = ax² + bx + c is (-b/2a, f(-b/2a)).
• Its axis of symmetry is x = -b/2a.
• Instead of using the formula x = -b/2a, we can convert the standard form f(x) = ax² + bx + c into vertex form f(x) = a (x - h)² + k by completing the square to find the vertex (h, k).
• The vertex of a parabola f(y) = ay² + by + c is (f(-b/2a), -b/2a).
• Its axis of symmetry is y = -b/2a.
• The vertex of a parabolic function f(x) = a (x - h)² + k is (h, k), where
• 'h' represents the horizontal shift and 'k' is the vertical shift of the parent function f(x) = x².
• A top/open parabola y = a(x - h)² + k has
• maximum value at the vertex (h, k) when a < 0 and
• minimum value at the vertex (h, k) when a > 0.
• A left/right open parabola has neither maximum nor minimum.
• We can use the vertex of a parabola to graph it. For this,
  Form a table of two columns labeled x and y with at least 5 rows. In the x-column, one of the numbers should be the x-coordinate of the vertex and two random numbers on each side (left and right) of it.
  Find the y-coordinate of each of the above five x-values by substituting each of them into the equation.
  Plot all the points and join them by a curve.

Examples on Vertex of a Parabola

Example 1: Does the vertex of each of the following parabolas is a maximum/minimum?
(a) y = 3x² - 4x + 5
(b) y = (-1/2)x² + 7

We know that y = ax² + bx + c

• opens up when a > 0 and hence it has a minimum at its vertex
• opens down when a < 0 and hence it has a maximum at its vertex

(a) By comparing y = 3x² - 4x + 5 with y = ax² + bx + c, we get a = 3.

Here a = 3 > 0 and hence it has a minimum at its vertex.

(b) By comparing y = (-1/2)x² + 7 with y = ax² + bx + c, we get a = (-1/2).
Here a = (-1/2) < 0 and hence it has a maximum at its vertex.

Example 2: Find the vertex of the parabola y = 0.5x² + 3x + 4.

Comparing the given equation with y = ax² + bx + c, we have a = 0.5, b = 3, and c = 4.
The x-coordinate of the vertex is, h = -b/2a = -3/2(0.5) = -3/1 = -3.
The y-coordinate of the vertex is, k = 0.5(-3)² + 3(-3) + 4 = -0.5.
The vertex of the given parabola is, (h, k) = (-3, -0.5)
Hence, The vertex of parabola = (-3, -0.5).

Example 3: What is the vertex of the parabola x = 3(y - 2) (y + 4)?

Comparing the equation with x = a (y - p) (y - q), we get p = 2 and q = -4.
Then the y-coordinate of the vertex, k = (p + q)/2 = (2 + (-4))/2 = -1.
The x-coordinate of the vertex is, h = 3 (-1 - 2) (-1 + 4) = 3(-3)(3) = -27
The vertex of the given parabola is, (h, k) = (-27, -1)
Hence, The vertex of parabola = (-27, -1).