Modulus Function | Mathematics for Digital SAT PDF Download

Introduction

• The modulus function, which is also called the absolute value function gives the magnitude or absolute value of a number irrespective of the number being positive or negative. It always gives a non-negative value of any number or variable. Modulus function is denoted as y = |x| or f(x) = |x|, where f: R → (0,∞) and x ∈ R.
• |x| is the modulus of x, where x is a real number. If x is non-negative then f(x) will be of the same value x. If x is negative, then f(x) will be the magnitude of x, that is, f(x) = -x if x is negative. Let us sum up the modulus function formula below.

Modulus Function Formula

The value of the modulus function is always non-negative. If f(x) is a modulus function, then we have:

• If x is positive, then f(x) = x
• If x = 0, then f(x) = 0
• If x < 0, then f(x) = -x

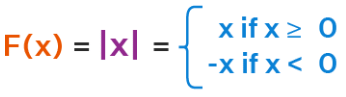
This means if the value of x is greater than or equal to 0, then the modulus function takes the actual value, but if x is less than 0 then the function takes minus of the actual value 'x'.

Domain and Range of Modulus Function

We can apply the modulus function to any real number. The range of the modulus function is the set of non-negative real numbers which is denoted as (0,∞) and the domain of the modulus function is R (where R refers to the set of all real numbers). Hence, the domain of the modulus function is R and the range is (0,∞).

Application of Modulus Function

Now, that we know the modulus function formula, let us consider a few examples to understand its application. The steps to calculate modulus function are given below:

Example: Consider the modulus function f(x) = |x|.

• If x = − 3, then y = f(x) = f(−3) = −(−3) = 3, here x is less than 0.
• If x = 3, then y = f(x) = f(3) = 3, here x is greater than 0
• If x = 0, then y = f(x) = f(0) = 0, here x is equal to 0

Note that f(-3) = f(3) here. In other words, |3| = |-3| = 3.

Graph of Modulus Function

Now let us see how to plot the graph for a modulus function. Let us consider x to be a variable, taking values from -5 to 5. Calculating modulus for the positive values of 'x', the line plotted in the graph is 'y = x' and for the negative values of 'x', the line plotted in the graph is 'y = -x'.

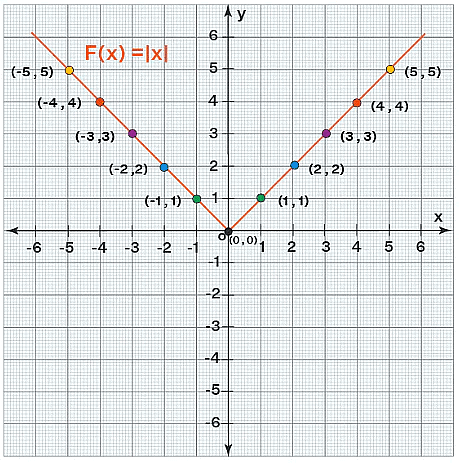
Properties of Modulus Function

Now, that we have the formula for the modulus function and the graph of the modulus function, let us now explore the properties of the modulus function:

• Property 1: The modulus function always gives a non-negative number as output for all real values of x. Thus, the modulus function is never equal to a negative number.
  • |x| = a; a > 0 ⇒ x = ± a ;
  • |x| = a; a = 0 ⇒ x = 0 ;
  • If |x| = a, then a can never be less than zero.
• Property 2:
  • Case 1: (If a > 0): Inequality for a positive number
    |f(x)| < a and a > 0 ⇒ −a < f(x) < a
    |f(x)| > a and a > 0 ⇒ −a < f(x) (or) f(x) > a
  • Case 2: (If a < 0): Inequality for a negative number
    |f(x)| < a and a < 0 ⇒ there is no solution for this.
    |f(x)| > a and a < 0 ⇒ this is valid for all real values of f(x).
• Property 3: If x,y are real numbers, then
  • |-x| = |x|
  • |x − y| = 0 ⇔ x = y
  • |x + y| ≤ |x| + |y|
  • |x − y| ≥ ||x| − |y||
  • |xy| = |x| |y|
  • |x/y| = |x|/|y|, y not equal to zero.

Derivative And Integral of Modulus Function

Since we know that a modulus function f(x) = |x| is equal to x if x > 0 and -x if x < 0, therefore the derivative of modulus function is 1 if x > 0 and -1 if x < 0. The derivative of the modulus function is not defined for x = 0. Hence the derivative of modulus function can be written as d(|x|)/dx = x/|x|, for all values of x and x not equal to 0.

Using the formula of the modulus function and integration formulas, the integral of the modulus function is (1/2)x² + C if x ≥ 0, and its integral is -(1/2)x² + C if x < 0. Hence the integration of the modulus function can be clubbed as:

• ∫|x| dx = (1/2)x² + C if x ≥ 0
• ∫|x| dx = -(1/2)x² + C if x < 0

Important Notes on Modulus Function

• The modulus function is also called the absolute value function and it represents the absolute value of a number. It is denoted by |x|.
• The domain of modulus functions is the set of all real numbers.
• The range of modulus functions is the set of all real numbers greater than or equal to 0.
• The vertex of the modulus graph y = |x| is (0,0).
• The vertex of the modulus function y = a |x - h| + k is (h, k).

Modulus Function Examples

Example 1: Find the value of the modulus function |x| for x = -5 and x = 10

If x = -5, then |x| = |-5| = 5
If x = 10, then |x| = |10| = 10

|x| = 5 for x = -5 and |x| = 10 for x = 10

Example 2: Solve |x + 3| = 8 using modulus function definition.

We know that the modulus function value is always non-negative, therefore we have two cases:
If x + 3 > 0, then |x + 3| = x + 3 and if x + 3 < 0, then |x + 3| = -(x + 3).
Case 1: If x + 3 > 0, we have
|x + 3| = x + 3
⇒ x + 3 = 8
⇒ x = 8 - 3 = 5
Case 2: If x + 3 < 0, we have
|x + 3| = -(x + 3)
⇒ -(x + 3) = 8
⇒ -x - 3 = 8
⇒ x = -3 - 8 = -11
Hence, the solution is x = 5, -11

Example 3: Solve the inequality |x - 1| < 3.

Here, 3 > 0. So by the properties of modulus function,
-3 < x - 1 < 3
Adding 1 on all the sides,
-3 + 1 < x < 3 + 1
-2 < x < 4
The solution of the given inequality is -2 < x < 4.