Prime Factorization | Mathematics for Grade 10 PDF Download

Prime factorization is a way of expressing a number as a product of its prime factors. A prime number is a number that has exactly two factors, 1 and the number itself. For example, if we take the number 30. We know that 30 = 5 × 6, but 6 is not a prime number. The number 6 can further be factorized as 2 × 3, where 2 and 3 are prime numbers. Therefore, the prime factorization of 30 = 2 × 3 × 5, where all the factors are prime numbers.

What is Prime Factorization?

The process of writing a number as the product of prime numbers is prime factorization. Prime numbers are the numbers that have only two factors, 1 and the number itself. For example, 2, 3, 5, 7, 11, 13, 17, 19, and so on are prime numbers. Prime factorization of any number means to represent that number as a product of prime numbers. For example, the prime factorization of 40 can be done in the following way: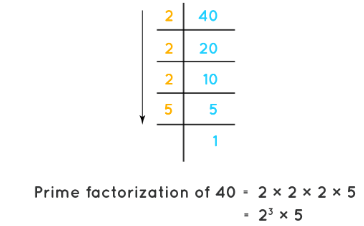

Prime Factorization Definition

The method of breaking down a number into its prime numbers that help in forming the number when multiplied is called prime factorization. In other words, when prime numbers are multiplied to obtain the original number, it is defined as the prime factorization of the number.

Prime Factorization of a Number

Let us see the prime factorization chart of a few numbers in the table given below:

What are Factors and Prime Factors?

Factors of a number are the numbers that are multiplied to get the original number. For example, 4 and 5 are the factors of 20, i.e., 4 × 5 = 20, whereas, prime factors of a number are the prime numbers that are multiplied to get the original number. For example: 2, 2, and 5 are the prime factors of 20, i.e., 2 × 2 × 5 = 20. It should be noted that all the factors of a number may not necessarily be prime factors.
Prime factorization is similar to factoring a number but it considers only prime numbers (2, 3, 5, 7, 11, 13, 17, 19, and so on) as its factors. Therefore, it can be said that factors that divide the original number completely and cannot be split into more factors are known as the prime factors of the given number.

Methods of Prime Factorization

There are various methods for the prime factorization of a number. The most common methods that are used for prime factorization are given below:

• Prime factorization by factor tree method
• Prime factorization by division method

Prime Factorization by Factor Tree Method
In the factor tree method, the factors of a number are found and then those numbers are further factorized until we reach the prime numbers. Let us understand the prime factorization of a number using the factor tree method with the help of the following example.
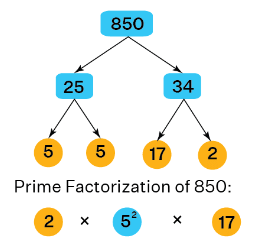
Example: Do the prime factorization of 850 using the factor tree.
Solution: Let us get the prime factors of 850 using the factor tree given below.

• Step 1: Place the number, 850, on top of the factor tree.
• Step 2: Then, write down the corresponding pair of factors as the branches of the tree. Here, they are 25 and 34.
• Step 3: Factorize the composite factors that are found in step 2, and write down the pair of factors as the next branches of the tree. Here, 25 can be further factorized into 5 × 5, and 34 can be factorized into 17 × 2
• Step 4: Repeat step 3, until we get the prime factors of all the composite factors. So, we get the prime factors of 850 = 2 × 5² × 17

Prime Factorization by Division Method

The division method can also be used to find the prime factors of a large number by dividing the number by prime numbers. Let us learn how to find the prime factors of a number by the division method using the following example.
Example: Do the prime factorization of 60 with the division method.

• Step 1: Divide the number by the smallest prime number such that the smallest prime number should divide the number completely. Here we divide 60 by 2 to get 30.
• Step 2: Again, divide the quotient of step 1 by the smallest prime number. S0, 30 is again divided by 2 and we get 15.
• Step 3: Repeat step 2, until the quotient becomes 1. Now, 15 is not divisible by 2, so we take the next prime number which is 3. And 15 ÷ 3 = 5. Then we divide 5 ÷ 5 = 1. Since we get 1 as the quotient, we stop here.
• Step 4: Finally, multiply all the prime factors that are the divisors. Prime factorization of 60 = 2 × 2 × 3 × 5

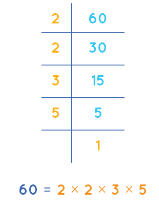
Therefore, the prime factors of 60 are 2, 3, and 5.

Applications of Prime Factorization

Prime factorization is used extensively in the real world. The two most important applications of prime factorization are given below.

• Cryptography and Prime Factorization
• HCF and LCM Using Prime Factorization

Cryptography and Prime Factorization

Cryptography is a method of protecting information using codes. Prime factorization plays an important role for the coders who create a unique code using numbers which is not too heavy for computers to store or process quickly.

HCF and LCM Using Prime Factorization

To find the Highest Common Factor (HCF) and the Least Common Multiple (LCM) of two numbers, we use the prime factorization method. For this, we first do the prime factorization of both the numbers. The following points related to HCF and LCM need to be kept in mind:

• HCF is the product of the smallest power of each common prime factor.
• LCM is the product of the greatest power of each common prime factor.

Example: What is the HCF and LCM of 850 and 680?
Solution: We will first do the prime factorization of both the numbers.

• The prime factorization of 850 is: 850 = 2¹ × 5² × 17¹
• The prime factorization of 680 is: 680 = 2³ × 5¹ × 17¹
• Observing this, we can see that the common prime factors of 850 and 680 with the smallest powers are 2¹, 5¹ and 17¹, and the common prime factors with the highest powers are 2³, 5², 17¹
• HCF is the product of the common prime factors with the smallest powers. Hence, HCF of (850, 680) = 2¹ × 5¹ × 17¹ = 170
• LCM is the product of the common prime factors with the highest powers. Hence, LCM of (850, 680) = 2³ × 5² × 17¹ = 3400
• Thus, HCF of (850, 680) = 170, LCM of (850, 680) = 3400