Polynomials in One Variable | The Complete SAT Course - Class 10 PDF Download
Polynomials in one variable are algebraic expressions that are of the form axn where n is a non-negative (i.e. positive or zero) integer and a is a real number, called the coefficient of the term. The degree of a polynomial in one variable is the largest exponent in the polynomial.
What are Polynomials in One Variable?
Polynomials in one variable are those expressions in which there is only one variable present. In mathematics, a polynomial is an expression that consists of variables and coefficients, involving the operations of addition, subtraction, multiplication, and exponentiation of variables. The word "polynomial" contains two words, namely, “poly" and “nomials”. "Poly" means many, and "nomials" means terms. Hence an expression containing many terms is called polynomials, having variables and coefficients.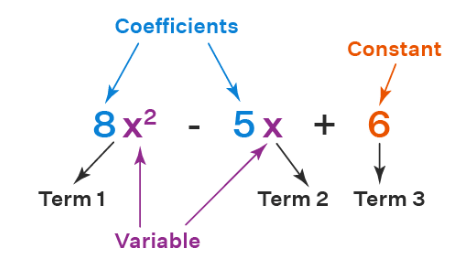
Some examples of polynomials in one variable are given below:
- x2 + 3x − 2
- 3y3 + 2y2 − y+ 1
- m4 − 5m2 + 8m − 3
Classification of Polynomials in One Variable
To learn about the classification of one variable polynomial based on degree, let us first understand the meaning of the degree of a polynomial. The highest power of the variable in a polynomial is called the degree of the polynomial. For example, in the following equation: x2 + 2 x + 4, the degree of the polynomial is 2, i.e., the highest power of the variable in the polynomial.
Based on the degree of a polynomial in one variable, it can be classified into 4 types:
- Zero or constant polynomial
- Linear polynomial
- Quadratic polynomial
- Cubic polynomial
For a multivariable polynomial, the degree is the highest sum of powers of different variables in any of the terms in the expression.
- Zero or Constant Polynomial
A polynomial having 0 as the degree of the polynomial is termed as zero or constant polynomial. Such polynomials only have constant terms with no variable. 2, which we can also write as 2x0, is an example of zero polynomial. - Linear Polynomial
A polynomial with 1 as the degree of the polynomial is termed a linear polynomial. Linear polynomials can have multiple variables. So, we consider linear polynomial in one variable as a type of polynomial in one variable. Examples - x + 7, 3y − 27, 7z + 17/2 - Quadratic Polynomial
A quadratic polynomial is a polynomial of degree 2, i.e, the highest exponent of the variable is 2. Examples - x2 + 7x + 12, 2m2 − 5m + 32, 8y2 − 2 - Cubic Polynomial
A cubic polynomial is a polynomial of degree 3, i.e, the highest exponent of the variable is 3. Examples - 4y3 − 8, x3 + 5x2 − 6x − 4, 5z3 − 3/4
How to Solve Polynomials in One Variable?
Solving polynomials refers to finding their roots. A root or zero of a polynomial is the value for which the given polynomial is equal to zero. The first step in solving any polynomial is to find its degree. As discussed above the degree of a polynomial with one variable is the largest exponent of that variable. Thus,
- Linear polynomials can have multiple variables but these polynomials have only one solution.
- Quadratic polynomials in one variable have only two solutions possible.
- Cubic polynomials in one variable have only three solutions possible.
Example: Find the perimeter of the square with side length 8x units. Also, state the type of polynomial obtained (based on the degree).
Solution: We know that the perimeter of a square is the sum of all its sides. In a square, all sides are equal. So, if we add all four sides of the square, we get, 8x + 8x + 8x + 8x, which equals 32x.
∴ The perimeter of the square is 32x units.
32x has only one variable with degree 1. So, it is a linear polynomial in one variable.
∴ The perimeter of the square is 32x units which is a linear polynomial in one variable.
|
433 videos|220 docs|166 tests
|





















