Polynomial Identities | Mathematics for ACT PDF Download

What is Polynomial Identity?

Polynomial identity refers to an equation that is always true, irrespective of the variable values. We use polynomial identities while factorising the polynomial or expanding the polynomial. To solve the polynomial equation easily, it is essential to learn some of the important polynomial identities which are listed below.

Important Polynomial Identities

The most important polynomial identities, also known as algebraic identities in Maths are:

• (a + b)² = a² + b² + 2ab
• (a - b)² = a² + b² - 2ab
• (a + b)(a - b) = a² - b²
• (x + a)(x + b) = x² +  x(a + b) + ab

Apart from the above-mentioned identities, there are other polynomial identities that are equally important while solving the expressions. They are:

• (a + b)³ = a³ + 3a²b + 3ab² + b³
• (a - b)³ = a³ - 3a²b + 3ab² - b³
• a³ + b³ = (a + b)(a² - ab + b²)
• a³ - b³ = (a - b)(a² + ab + b²)
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

Proof of Polynomial Identities

Here, we are going to discuss the proofs of the above-mentioned polynomial identities, one by one.

Identity 1: (a + b)² = a² + b² + 2ab

Here, (a + b)² is nothing but the product of (a + b) and (a + b).
(i.e) (a + b)² = (a + b)×(a + b)
So, this can be visualised as a square whose side is a + b and its area is given by (a + b)².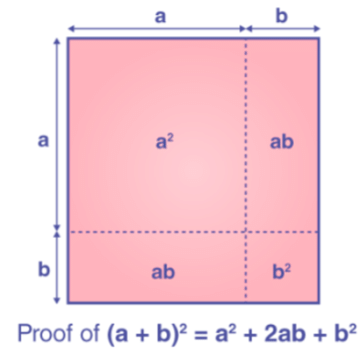

From the figure, we can say that the area of a square (a + b)² is equal to the sum of the individual squares and rectangles.
Hence, (a + b)² = a² + b² + 2ab is proved.

Identity 2: (a - b)² = a² + b

²

- 2ab

Let us assume that (a - b)² is the area of a square of length (a - b). To understand this, let us start with the larger square of area “a²”. Reduce all the sides of a square by length “b”. Now, remove the extra bits from a2 and we are left with (a - b)², which is represented by the yellow area.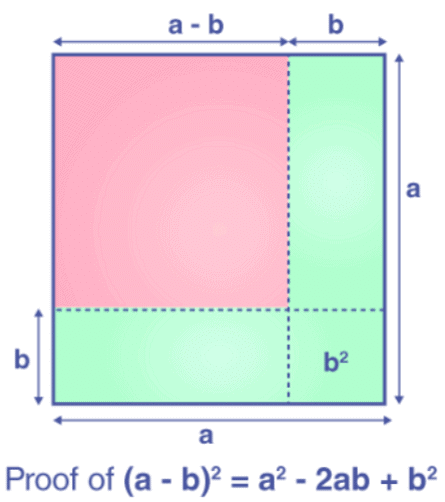

So, to get the yellow area from the larger blue square, subtract the horizontal and vertical strips which have the area ab. However, removing ab twice will also eliminate the overlapping square at the bottom right side corner twice. So, we add b².
Hence, (a-b)² = a² + b² - 2ab is proved.

Identity 3: (a + b)(a - b) = a² - b²

Assume that (a+b)(a-b) is the area of a rectangle whose sides are (a+b) and (a-b).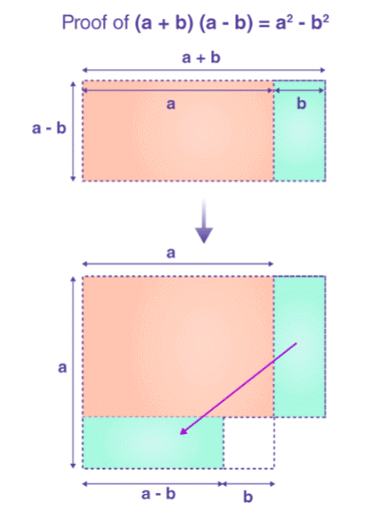

Thus, by rearranging the individual squares and rectangles, we will get (a + b)(a - b) = a² - b². Hence, proved.

Identity 4: (x + a)(x + b) = x² + x(a + b) + ab

Let us assume that (x + a)(x + b) is the area of a rectangle whose sides are (x + a) and (x + b).

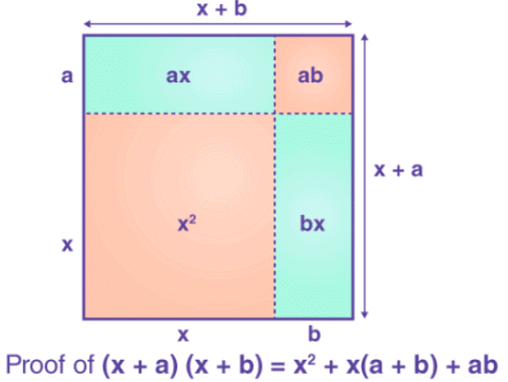
Thus, the area of a rectangle in terms of individual squares and rectangles is x² + ax + bx + b².
Hence, (x + a)(x + b) = x² + x(a + b) + b² is proved.