Diagonal Length of a Cube | Mathematics for ACT PDF Download

The diagonal of a cube formula helps in calculating the lengths of the different diagonals of a cube - the face diagonals and the body diagonals. A cube is a three-dimensional solid figure, also known as the square solid that has all edges of the same measure. This means that the length, width, and height of a cube is of equal measure, and each of its faces is a square. 

What is Diagonal of a Cube?

The diagonal of a cube is the line segment that connects any two non-adjacent vertices of the cube. Cube is one of the important geometric shapes because this 3D shape has all 12 equal edges and it is one of the most commonly seen shapes around us. Some of the real-life examples of a cube are ice cubes, sugar cubes, Rubik's cubes, playing dice, etc. There are two kinds of diagonals in a cube because it is a three-dimensional figure.

• Face Diagonal of a Cube
  A cube has 6 square-shaped faces. There are 2 diagonals on each face joining the non-adjacent vertices. Hence, there are 12 face diagonals in a cube.
• Body Diagonal of a Cube
  The body diagonals connect the opposite vertices of the cube passing through the body of the cube. Hence, there are 4 body diagonals in a cube that pass through the cube connecting the opposite corners.
• Diagonal of Cube Formula
  The length of the diagonals of a cube can be calculated according to the given parameters and requirements.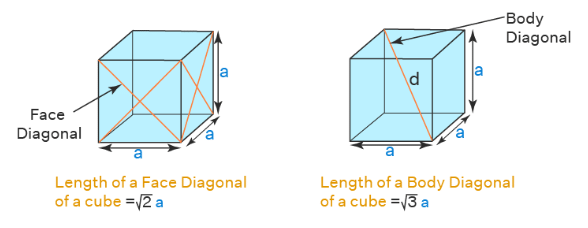
  

Length of Face Diagonal of a Cube

The formula that is used to calculate the length of a face diagonal of a cube is expressed as,
Length of each face diagonal of cube = √2a, where a = Length of each side of a cube.

Example: Find the length of the face diagonal of a cube if its side length is 6 cm.

Given, side length of the cube (a) = 6 cm, Face diagonal = ?
Length of each face diagonal of cube = √2a
So, let us substitute the given value in the formula.
Length of each face diagonal of cube = √2a
⇒ √2a ⇒√2 × 6 = 8.48 cm
Therefore, the length of the face diagonal is 8.48 cm

Length of Body Diagonal of a Cube

The formula that is used to calculate the length of a space or body diagonal of a cube is given as,
Length of each body diagonal of a cube = √3a, where a = Length of each side of a cube.

Example: Find the length of the body diagonal of a cube if its side length is 7 inches.

Given, side length of the cube (a) = 7 inches, Body diagonal = ?
Length of each body diagonal of cube = √3a
So, let us substitute the given value in the formula.
Length of each body diagonal of cube = √3a
⇒ √3a ⇒√3 × 7 = 12.12 inches.
Therefore, the length of the body diagonal is 12.12 inches

Derivation of Diagonal of a Cube Formula

The diagonal of a cube formula usually refers to the body diagonal of the cube. This formula can be derived by using the Pythagoras theorem. Let us consider the side of the cube as 'a', a face diagonal as r, and body diagonal as d. Once we join the face diagonal and the body diagonal, we can see that a right-angled triangle is formed with sides a, r, and d. The body diagonal becomes the hypotenuse of the right-angled triangle that is formed.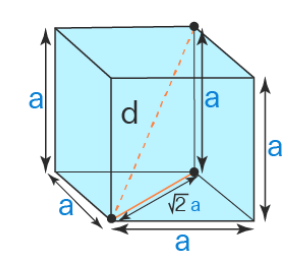

By using the Pythagoras theorem, we have a² + r² = d² (let us keep this as equation 1)
We already know that the face diagonal is √2a so, 'r' can be replaced by √2a, this means 'r' = √2a
By substituting the value of r in equation 1, we get
a² + (√2a)² = d²
a² + 2a² = d²
3a² = d²
d = √(3a²)
d = √3a
Therefore, the diagonal of a cube formula = √3a

Example Using Diagonal of a Cube Formula

Example: Calculate the length of the body diagonal of a cube whose each side measures 5 units.

Given, length of each side of the cube (a) = 5 units; body diagonal = ?
So, let us substitute the given values in the formula,
Length of body diagonal of a cube = √3a
= √3 × 5 = 8.66 units
Therefore, the length of the body diagonal of the given cube = 8.66 units.