Volume of a Pyramid | Mathematics for Digital SAT PDF Download

The volume of pyramid is space occupied by it (or) it is defined as the number of unit cubes that can be fit into it. A pyramid is a polyhedron as its faces are made up of polygons. There are different types of pyramids such as a triangular pyramid, square pyramid, rectangular pyramid, pentagonal pyramid, etc that are named after their base, i.e., if the base of a pyramid is a square, it is called a square pyramid. All the side faces of a pyramid are triangles where one side of each triangle merges with a side of the base.

What is Volume of Pyramid?

The volume of a pyramid refers to the space enclosed between its faces. It is measured in cubic units such as cm³, m³, in³, etc. A pyramid is a three-dimensional shape where its base (a polygon) is joined to the vertex (apex) with the help of triangular faces. The perpendicular distance from the apex to the center of the polygon base is referred to as the height of the pyramid. A pyramid's name is derived from its base. For example, a pyramid with a square base is referred to as a square pyramid. Thus, the base area plays a major role in finding the volume of a pyramid. The volume of the pyramid is nothing but one-third of the product of the base area times its height.

Volume of Pyramid Formula

Let us consider a pyramid and prism each of which has a base area 'B' and height 'h'. We know that the volume of a prism is obtained by multiplying its base by its height. i.e., the volume of the prism is Bh. The volume of a pyramid is one-third of the volume of the corresponding prism (i.e., their bases and heights are congruent). Thus,

Volume of pyramid = (1/3) (Bh), where

• B = Area of the base of the pyramid
• h = Height of the pyramid (which is also called "altitude")

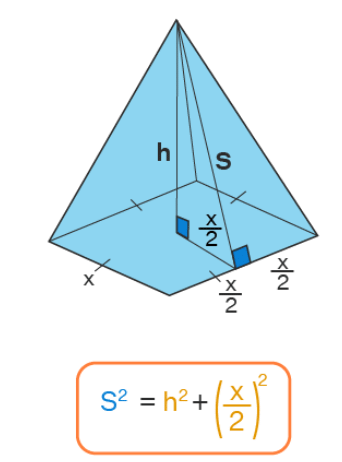
Note: The triangle formed by the slant height (s), the altitude (h), and half the side length of the base (x/2) is a right-angled triangle and hence we can apply the Pythagoras theorem for this. Thus, (x/2)²  + h² = s² . We can use this while solving the problems of finding the volume of the pyramid given its slant height.

Volume Formulas of Different Types of Pyramids

From the earlier section, we have learned that the volume of a pyramid is (1/3) × (area of the base) × (height of the pyramid). Thus, to calculate the volume of a pyramid, we can use the areas of polygons formulas (as we know that the base of a pyramid is a polygon) to calculate the area of the base, and then by simply applying the above formula, we can calculate the volume of pyramid. Here, you can see the volume formulas of different types of pyramids such as the triangular pyramid, square pyramid, rectangular pyramid, pentagonal pyramid, and hexagonal pyramid and how they are derived.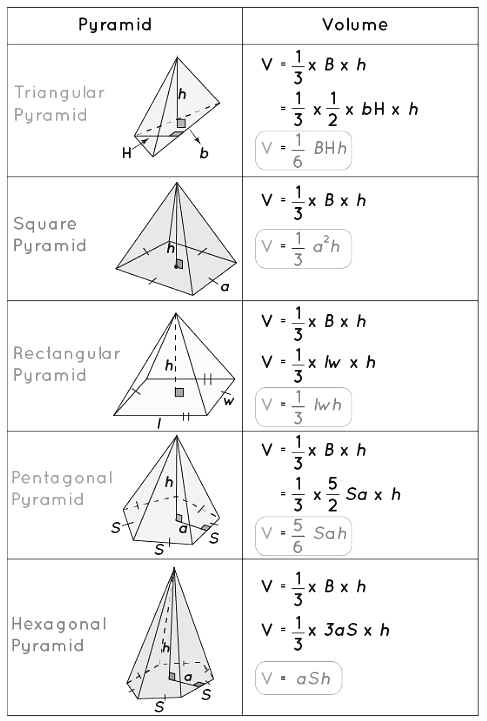

Example: Tim built a rectangular tent (that is of the shape of a rectangular pyramid) for his night camp. The base of the tent is a rectangle of side 6 units × 10 units and the height is 3 units. What is the volume of the tent?

The base area (area of rectangle) of the tent is, B = 6 × 10 = 60 square units.
The height of the tent is h = 3 units.
The volume of the tent using the volume of pyramid formula is,
V = (1/3) (Bh)
V = (1/3) × 60 × 3
V = 60 cubic units.