Area & Volume of Sphere | The Complete SAT Course - Class 10 PDF Download
| Table of contents |

|
| Area & Volume of Sphere |

|
| Difference Between Circle and Sphere |

|
| Surface Area of a Hemisphere |

|
| Volume of Hemisphere |

|
A sphere is a three-dimensional object that is round in shape. The sphere is defined in three axes, i.e., x-axis, y-axis and z-axis. This is the main difference between circle and sphere. A sphere does not have any edges or vertices, like other 3D shapes.
The points on the surface of the sphere are equidistant from the center. Hence, the distance between the center and the surface of the sphere are equal at any point. This distance is called the radius of the sphere. Examples of spheres are a ball, a globe, the planets, etc.
What is a Sphere?
As discussed in the introduction, the sphere is a geometrical figure that is round in shape. The sphere is defined in a three-dimensional space. The sphere is three dimensional solid, that has surface area and volume. Just like a circle, each point of the sphere is at an equal distance from the center.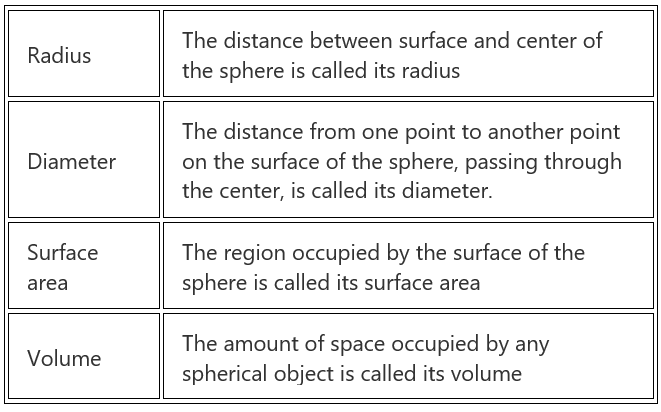
In the above figure, we can see, a sphere with radius ‘r’.
Unlike a circle, which is a plane shape or flat shape, defined in XY plane, a sphere is defined in three dimensions, i.e. x-axis, y-axis and z-axis.
Important Facts on Sphere
- A sphere is a symmetrical object
- All the surface points of the sphere are equidistant from center
- A sphere has an only a curved surface, no flat surface, no edges and no vertices
Shape of Sphere
The shape of a sphere is round and it does not have any faces. The sphere is a geometrical three-dimensional solid having a curved surface. Like other solids, such as cube, cuboid, cone and cylinder, a sphere does not have any flat surface or a vertex or an edge.
The real-life examples of the sphere are:
- Basketballs
- World Globe
- Marbles
- Planets
- Moon
Properties of a sphere
The important properties of the sphere are given below. These properties are also called attributes of the sphere.
- A sphere is perfectly symmetrical
- A sphere is not a polyhedron
- All the points on the surface are equidistant from the center
- A sphere does not have a surface of centers
- A sphere has constant mean curvature
- A sphere has a constant width and circumference.
Equation of a Sphere
In analytical geometry, if “r” is the radius, (x, y, z) is the locus of all points and (x0, y0, z0) is the center of a sphere, then the equation of a sphere is given by:
(x -x0)2 + (y – y0)2 + (z-z0)2 = r2
Sphere Formulas
The common formulas of the sphere are:
- Surface area
- Volume

Surface Area of a Sphere
The surface area of a sphere is the total area covered by the surface of a sphere in a three-dimensional space. The formula of surface are is given by:
The Surface Area of a Sphere(SA) = 4πr2 Square units
Where “r” is the radius of the sphere.
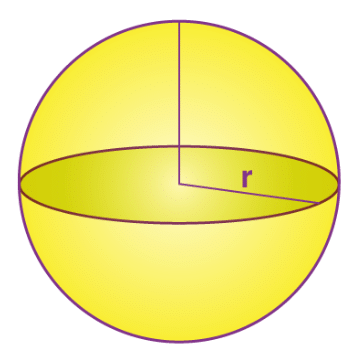
Volume of a Sphere
The amount of space occupied by the object three-dimensional object called a sphere is known as the volume of the sphere.
According to the Archimedes Principle, the volume of a sphere is given as,
The volume of Sphere(V) = 4/3 πr3 Cubic Units
Difference Between a Sphere and a Circle
A circle and a sphere are shapes in geometry, that appear the same, but are different in properties. The key differences between the two shapes are listed below in the table.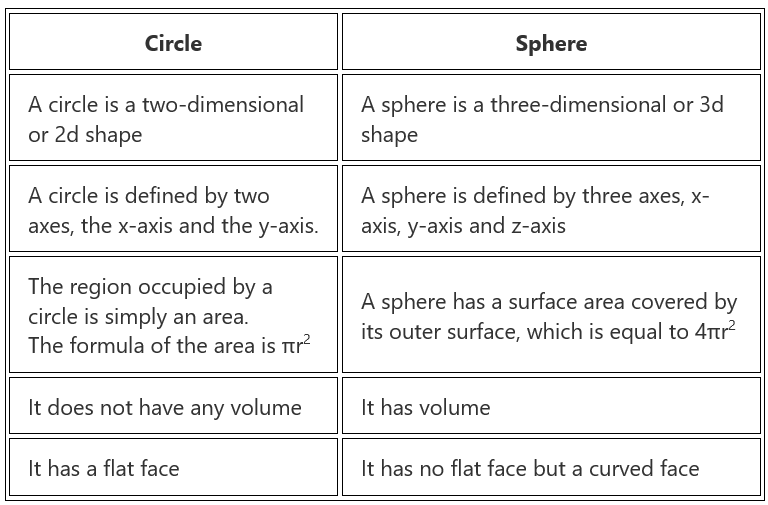
Area & Volume of Sphere
Area of sphere or total surface area of sphere is the region covered by a surface of a spherical object in a three-dimensional space. Since the sphere is a complete curved shape therefore the curved surface area is equal to the total area of sphere. It is also called lateral surface area.
Surface Area of Sphere = 4πr2, where r is the radius of sphere.
A sphere is a solid figure bounded by a curved surface such that every point on the surface is the same distance from the centre. In other words, a sphere is a perfectly round geometrical object in three-dimensional space, just like a surface of a round ball. The distance from the center to the outer surface of sphere is called its radius. The surface area of a sphere is defined as the amount of region covered by the surface of a sphere and is equal to 4πr2. The volume of sphere is the space occupied by it in 3d space.
What is the Sphere?
A sphere is mathematically defined as the set of points that are all at the same distance from a given point but in three-dimensional space. The distance from the centre to the outermost surface is called the radius of the sphere and the line that connects two points on the sphere and is twice the length of the radius is called diameter.
Diameter = 2 x radius
Sphere Properties
Some of the important properties of sphere are as follows:
- Sphere has no face and edge
- A sphere is perfectly symmetrical
- It is not a polyhedron
- All the points on the surface are equidistant from the centre of the sphere.
- It has only one surface (but not the face)
Surface Area of Sphere
A sphere is the 3- D shape where the curved surface area equals to the total surface area of the figure. The curved surface area is the area in which only the area of the curved part is covered. The formula does not take into account the circular base. The total surface area, on the other hand, is a combination of the curved area along with the area of the base The formula for the total surface area and the curved surface area of the sphere is given below
Surface area (TSA) = CSA = 4πr2 square units
How to Find Area of a Sphere?
To find the area of the sphere firstly, follow the below steps:
- Find the radius of the sphere
- Mention the value of radius in the surface area formula, i.e. (4πr2)
- Solve the expression and evaluate the final value
Area of Hemisphere
Hemisphere is also a 3d shape, which is just half of the sphere. When a plane cuts the sphere in two equal halves, we get a hemisphere.
The total surface area (TSA) of hemisphere is equal to the sum of its curved surface area and base area (circular base).
Therefore,
TSA (hemisphere) = Half of area of sphere + Base area
TSA = 2πr2 + πr2
TSA = 3πr2
Volume of Sphere
The volume of the sphere is defined as the number of cubic units needed to fill a sphere. The formula for volume of sphere is given by:
Volume = 4/3 πr3 (Cubic Units)
Unit: S.I unit is given cubic meters ( m3)
The derivation is given as:
V=Volume of the Sphere
= Sum of the volumes of all pyramids
= 1/3A1r + 1/3A2r + 1/3A3r+….+1/3Anr
= 1/3(Surface area of the sphere) r
=1/3(4πr2)×r
=4/3(πr3)
In the above derivation, the sphere in Fig:2 is divided into pyramids, and the volume of the sphere is equal to the volume of all the pyramids as shown in the figure. The total volume is calculated by the summation of the pyramids volumes.
How to Find Volume of Sphere?
Steps for Finding the Volume of a Sphere:
- Step 1: Find the radius of a sphere and cubic it.
- Step 2: Take the product of 4/3 π and the cube of the radius of the sphere.
- Step 3: Write the answer in the proper cubic unit of measurement.
Example: Find the volume of a sphere of diameter 12 m, rounding your answer to two decimal places(using pi = 3.14).
Diameter of the sphere (d) = 12 m
Step 1:
Find the radius of the sphere:
Radius of the sphere (r) = d/2 = 12/2 = 6 m
Step 2:
Volume of the sphere (V) = 4/3 π r3
V = 4/3 x 3.14 x 63
V = 4/3 x 3.14 x 6 x 6 x 6
V = 904.32
Hence the volume of the sphere is 904.32 m3.
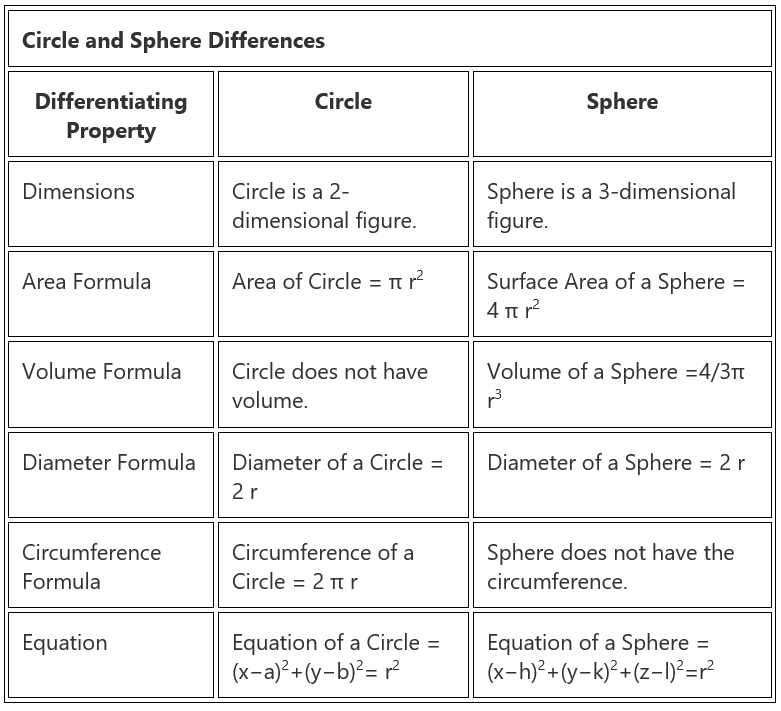
Difference Between Circle and Sphere
There are a few fundamental differences between a circle and sphere which separates them in a lot of ways. Both the circle and sphere are different, even if they are circular objects. Thus, they create a lot of confusion in understanding them. Both seem to be similar, but in reality, they have a vast difference between them. Let us have a deeper understanding of both the terms.
Definition of Circle and Sphere
- A Circle is a two-dimensional figure whereas, a Sphere is a three-dimensional object.
- Area of a Circle = π r2 and Area of a Sphere = 4 π r2
- A circle has no volume and the Volume of a Sphere =4/3π r3
- A circle has all points at the same distance from its centre along a plane, whereas in a sphere all the points are equidistant from the centre at any of the axes.
- We can only determine the area in case of a Circle, while in Sphere, we can calculate the surface area as well as volume.
What is the Difference Between Sphere and Circle?
Equation of Sphere
A sphere is defined as a completely round geometrical object in a three-dimensional space just like a round ball. To be geometrical, a sphere is a set of points that are equidistant from a point in space. The distance between the outer point and centre of the sphere is called the radius, denoted by r and the maximum straight distance between any two sides of the sphere through the centre is known as the diameter, denoted by d.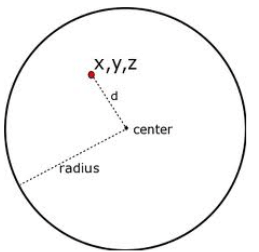
A hemisphere is exactly half of a sphere which can only be obtained when a sphere is split from the middle. The biggest circle of a sphere is a circle that has the same centre and radius of a sphere. A great circle of the sphere is a circle that has the same radius and centre as the sphere itself. In this article, let us discuss how to derive the equation of a sphere along with the surface area and the volume of the sphere in detail.
How to Derive the Equation of a Sphere?
The equation of a circle of radius r is given by:
x2 + y2 = r2
You can relate it to the algebraic method of starting the Pythagoras theorem.
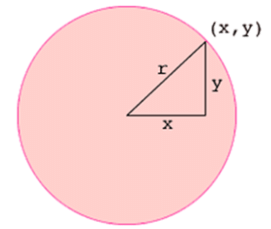
The point (x, y) lies on the circle only when the right triangle has sides of length |x| and |y| and hypotenuse of length r, which can be written as:
x2 + y2 = r2
Pythagoras theorem can be used twice for the equation of a sphere. In the below figure, O is the origin and P(x, y, z) is a point in three-space. P is on the sphere with radius r only when the distance from O to P is r.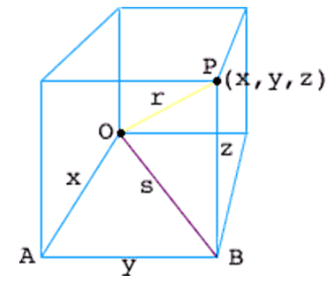
Since OAB is a right angle triangle, x2 + y2 = s2. The triangle OBP is another right triangle and therefore, s2 + z2 = r2. Hence, the distance between O and P can be expressed by:
x2 + y2 + z2 = |OP|2
Hence, we can conclude that (x, y, z) lies on the sphere with radius r only if,
x2 + y2 + z2 = r2
which is called the equation of a sphere.
If (a, b, c) is the centre of the sphere, r represents the radius, and x, y, and z are the coordinates of the points on the surface of the sphere, then the general equation of a sphere is (x – a)2 + (y – b)2 + (z – c)2 = r2
Volume of a Sphere Equation
The formula to calculate the volume of a sphere is given by the equation:
The volume of the sphere = 4/3 πr3
Where r is the radius of the sphere.
Surface Area of a Sphere Equation
The formula to calculate the surface area of the sphere is given by:
The Surface area of the sphere = 4 πr2 square units.
Example: Write the equation of the sphere in the standard form where the centre and radius of the sphere are given as (11, 8, -5) and 5 cm respectively.]
Given: Centre = (11, 8, -5) = (a, b, c)
Radius = 5 cm
We know that the equation of the sphere in the standard form is written as:
(x-a)2 + (y-b)2 + (z-c)2 = r2
Now, substitute the given values in the above form, we get:
(x-11)2 + (y-8)2 + (z -(-5))2 =52
(x-11)2 + (y-8)2 + (z +5)2 = 25
Thus, the equation of the sphere is (x-11)2 + (y-8)2 + (z +5)2 = 25
Surface Area of a Hemisphere
In mathematics, two-dimensional geometry deals with the x-y plane. The extension of 2D geometry is the three-dimensional geometry which deals with three axes, namely x, y and z in the cartesian plane. 3D shapes have three different dimensions like length, breadth and height.
We have learned different types of three-dimensional shapes. In general, the three-dimensional objects are obtained by rotating the two-dimensional objects. Our earth is one of the best examples of 3D shapes, which is spherical in shape. The sphere is obtained from the rotation of 2D shape called the circle.
Hemisphere Definition
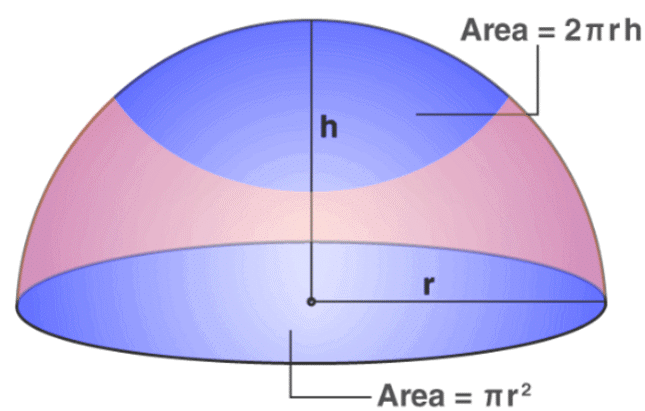
A sphere is a three-dimensional solid where all the points lying on the surface is equidistant from the centre. A hemisphere is formed when the plane cuts the sphere into two equal halves. A sphere is a combination of the two hemispheres.
Hemisphere Surface Area
We can easily find the surface area of a hemisphere since the base of the sphere is circular in shape. Generally, there are two different types of surface area. One is the total surface area, and the other is the curved surface area.
Curved Surface Area: The area of the outer surface of the hemisphere is called the curved surface area.
Total Surface Area: The area of the curved surface and the area of the circle (base) is called the total surface area
From the surface area of a sphere, we can easily calculate the surface area of the hemisphere.
Since hemisphere is half of the sphere
CSA of hemisphere = (1/2)surface area of the sphere
CSA = (1/2)4πr2
CSA = 2πr2
The curved surface area of a hemisphere = 2πr2 square units.
The total surface area of the sphere = Curved surface area of sphere + base area
We know that the base of the hemisphere is circular in shape, use the area of the circle.
TSA = 2πr2 + πr2 = 3πr2
Therefore,
The total surface area of a hemisphere = 3πr2 square units
Where π is a constant whose value is equal to 3.14 approximately.
“r” is the radius of the hemisphere.
Volume of Hemisphere
In geometry, we have studied different types of three-dimensional shapes. In three-dimensional shapes, the solids have three different measurements or dimensions like length, breadth and height. We know that 3D shapes do not lie on a piece of paper. Usually, most of the three-dimensional objects are obtained from the rotation of the two-dimensional objects. One of the best examples of the 3D shape is the sphere which is obtained from the rotation of 2D shape called the circle. Our earth is a good example of a sphere which is spherical.
Hemisphere Definition
A sphere is defined as a set of points in three-dimension, and all the points lying on the surface is equidistant from the centre. When a plane cuts across the sphere at the centre or equal parts, it forms a hemisphere. We can say, a hemisphere is exactly half of a sphere. In general, a sphere makes exactly two hemispheres. One such good example of the hemisphere is our earth. Our earth consists of two hemispheres, namely Southern Hemisphere and the Northern Hemisphere.
Hemisphere Volume
We can easily find the volume of the hemisphere since the base of the sphere is circular. The volume of the hemisphere is derived by Archimedes.
The volume of a hemisphere = (2/3)πr3 cubic units.
Where π is a constant whose value is equal to 3.14 approximately.
“r” is the radius of the hemisphere.
Hemisphere Equation
When the radius “R” is centred at the origin, it is given by
x2 + y2 + z2 = R2
The Cartesian form or equation of a hemisphere with the radius “R” at the point (x0, y0, z0) is written as
(x-x0)2 + (y- y0)2 + (z- z0)2 = R2
Therefore, the spherical coordinates of the hemisphere are given as follows
x = r cos θ sin ∅
y = r sin θ cos ∅
z = r cos ∅
|
433 videos|220 docs|166 tests
|




















