Direction Cosines of a Line | Mathematics for Digital SAT PDF Download

In simple words, the cosines of the angles made by a directed line segment with the coordinate axes are called as the direction cosines of that line.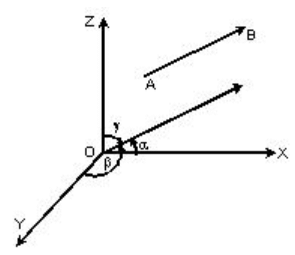

As illustrated in the figure above, if α, β, and γ are the angles made by the line segment with the coordinate axis then these angles are termed to be the direction angles and the cosines of these angles are the direction cosines of the line. Hence, cos α, cos β and cos γ are called as the direction cosines and are usually denoted by l, m and n.
l = cos α, m = cos β and n = cos γ
Another concept related to direction cosines is that of direction ratios. Three numbers which are proportional to the direction cosines of a line are called as the direction ratios. Hence, if ‘a’, ‘b’ and ‘c’ are the dr’s and l, m, n are the dc’s then, we must have
a/l = b/m = c/n.
This concept has been discussed in detail in the coming sections.

Some Key Points of Direction Cosines

• Since l = cos α, m = cos β and n = cos γ and we know that -1< cos x< 1 ∀ x ∈ R, so l, m and n are real numbers with values varying between -1 to 1. So, dc’s ∈ [-1,1].
• The angles made by the x-axis with the coordinate axis are 0°, 90° and 90°. Hence, the direction cosines are cos 0°, cos 90° and cos 90° i.e. 1, 0, 0.
• The dc’s of a, y and z axis are (1,0,0), (0,1,0) and (0,0,1).
• The direction cosines of a line parallel to any coordinate axis are equal to the direction cosines of the corresponding axis.
• The dc’s are associated by the relation l² + m² + n² =1.
• If the given line is reversed, then the direction cosines will be cos (π − α), cos (π − β), cos (π − γ) or − cos α, − cos β, − cos γ.
• Thus, a line can have two sets of dc’s according to its direction.
• The direction cosines of two parallel lines are always the same.  
• Direction ratios are proportional to direction cosines and hence for a given line, there can be infinitely many direction ratios.

Relation Between the Direction Cosines

Let OP be any line through the origin O which has direction cosines l, m, n.
Let P be the point having coordinates (x, y, z) and OP = r
Then OP² = x² + y² + z² = r²              …. (1)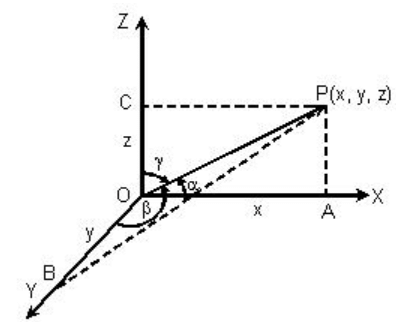

From P draw PA, PB, PC perpendicular on the coordinate axes, so that OA = x, OB = y, OC = z.
Also, ∠POA = α, ∠POB = β and ∠POC = γ.
From triangle AOP, l = cos α = x/r ⇒ x = lr
Similarly y = mr and z = nr
Hence from (1) r² (l² + m² + n²) = x² + y² + z² = r² 
 ⇒ l² + m² + n² = 1 

Direction Cosines of a Line Joining Two Points

If we have two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂), then the dc’s of the line segment joining these two points are
(x₂-x₁)/PQ, (y₂-y₁)/PQ , (z₂-z₁)/PQ
i.e. (x₂-x₁)/√Σ(x₂-x₁)², (y₂-y₁)/√Σ(x₂-x₁)², (z₂-z₁)/√Σ(x₂-x₁)² 

Example: A line with positive direction cosines passes through the point P(2, -1, 2) and makes equal angles with the coordinate axis. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals

The direction cosines are l = m = n = 1/√3.
Hence, the equation of the required line is
(x-2)/(1/√3) = (y+1)/(1/√3) = (z-2)/(1/√3)
Hence, this gives x-2 = y+1 = z-2 = r
Hence, any point on the line is Q = (r+2, r-1, r+2).
Since Q lies on the plane 2x + y + z = 9
Therefore 2(r+2) + (r-1) + (r+2) = 9
This yields 4r + 5 = 9 or r = 1.
Hence teh coordinates of Q are (3,0,3).
Hence, PQ = √[(3-2)² + (0+1)² + (3-2)²]
=  √3