Trigonometric Table | Mathematics for Digital SAT PDF Download

What is Trigonometric Table?

• The Trigonometric Table is simply a collection of the values of trigonometric ratios for various standard angles including 0°, 30°, 45°, 60°, 90°, sometimes with other angles like 180°, 270°, and 360° included, in a tabular format. 
• Because of patterns existing within trigonometric ratios and even between angles, it is easy to both predict the values of the trigonometry table and use the table as a reference to calculate trigonometric values for various other angles. The trigonometric functions are namely sine function, cosine function, tan function, cot function, sec function, and cosec function.

Trigonometric Values

• Trigonometry deals with the relationship between the sides of a triangle (right-angled triangle) and its angles. The trigonometric value is a collective term for values of different ratios, such as sine, cosine, tangent, secant, cotangent, and cosecant in a trigonometric table. All the trigonometric ratios are related to the sides of a right-angle triangle and their values are found using the following ratios.

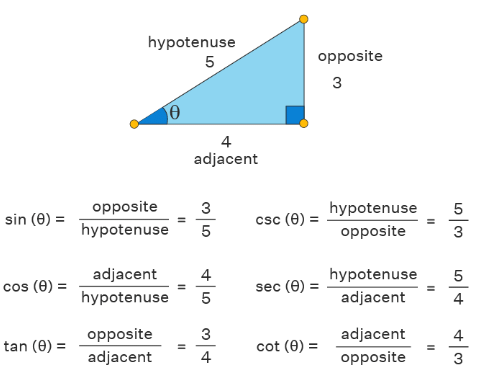
To remember this easily remember the word "SOHCAHTOA"!

• SOH
  Sine = Opposite / Hypotenuse
• CAH
  Cosine = Adjacent / Hypotenuse
• TOA
  Tangent = Opposite / Adjacent

Standard Angles in a Trigonometric Table

• The values of trigonometric ratios for the angles 0°, 30°, 45°, 60°, and 90° in a trigonometry table are commonly used to solve the trigonometry problems. These values are associated with the measurement of the lengths and the angles of a right-angle triangle. Thus, 0°, 30°, 45°, 60°, and 90° are called the standard angles in trigonometry.

Trigonometry Table for Standard Angles

• The trigonometric table is simply a collection of values of trigonometric functions of various standard angles including 0°, 30°, 45°, 60°, 90°, along with with other angles like 180°, 270°, and 360° included, in a tabular format. It is easy to predict the values of the trig ratios in a trigonometric table and to use the table as a reference to calculate trigonometric values for various other angles, due to the patterns existing within trigonometric ratios and even between angles.
• The table consists of trigonometric ratios – sine, cosine, tangent, cosecant, secant, and cotangent. In short, these ratios are written as sin, cos, tan, cosec, sec, and cot. It is best to remember the values of the trigonometric ratios of these standard angles.

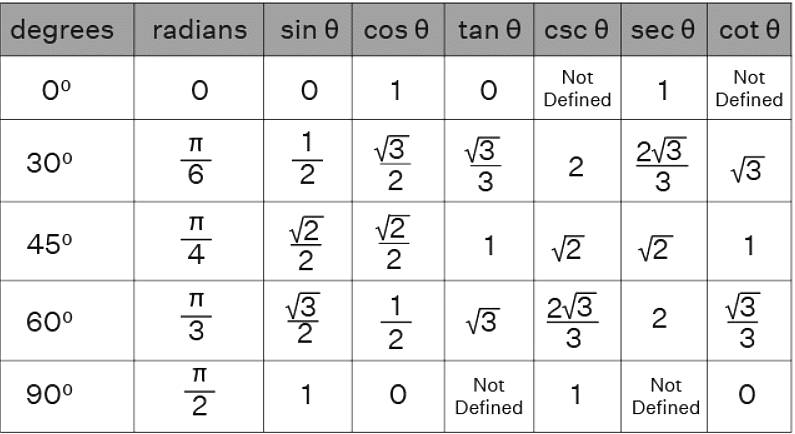
• Using the above table, values of sin π/6, cos π/6, tan π/6, sin π/4, cos π/4, tan π/4, sin π/3, cos π/3, tan π/3, sin π/2, cos π/2, and tan π/2 in radians could be easily found out. A trigonometric table has wide application in fields like science and engineering.

A few key points that can be noted in the trigonometric table are,

• The values for complementary angles present like 30° and 60° in a trigonometric table can be computed using complementary formulas for the various trigonometric ratios.
• The value for some ratios in a trig table is given as ∞ or "not defined". The reason for this is that while computing the values, a "0" appears in their denominator, so the value becomes undefined and is said to be equivalent to infinity.
• There is a sign change in the values in various places under 180°, 270°, etc for values of some trig ratios in a trigonometric table. This is due to the change in the quadrant.

How to Learn Trigonometric Table?

• The trigonometric table might seem complex at first, but it can be learned easily by only the values of sine for the 8 standard angles. Before generating the table, there are few formulas that must be followed as given below,
  • tan x = sin x/cos x
  • cosec x = 1/sin x
  • sec x = 1/cos x
  • cot x = 1/tan x

Given below are the steps to create and remember a trigonometric table.

• Step 1: Create a table with the top row listing the angles such as 0°, 30°, 45°, 60°, 90°, and write all trigonometric functions in the first column such as sin, cos, tan, cosec, sec, cot.
• Step 2: Determining the value of sin: Write the angles 0°, 30°, 45°, 60°, 90° in ascending order and assign them values 0, 1, 2, 3, 4 according to the order. So, 0° ⟶ 0; 30° ⟶ 1; 45° ⟶ 2; 60° ⟶ 3; 90° ⟶ 4. Then divide the values by 4 and square root the entire value. 0° ⟶ √0/2; 30° ⟶ 1 /2; 45° ⟶ 1/ √2; 60° ⟶ √3/2; 90° ⟶ √(4/4). This gives the values of sine for these 5 angles. Now for the remaining three use:
  • sin (180° − x) = sin x
  • sin (180° + x) = -sin x
  • sin (360° − x) = -sin x

This means,

• sin (180° − 0º) = sin 0º
• sin (180° + 90º) = -sin 90º
• sin (360° − 0º) = -sin 0º

• Step 3: Determining the value of cos: sin (90° – x) = cos x. Use this formula to compute values for cos x. For example, cos 45° = sin (90° – 45°) = sin 45°. Similarly, cos 30° = sin (90° - 30°) = sin 60°. Using this, you can easily find out the value of cos function as,
  
  

• Step 4: Determining the value of tan: (tan x = sin x/cos x). Hence, the value of tan function can be generated as,
  

• Step 5: Determining the value of cot: (cot x = 1/tan x). Use the relation to generate the cot function as,
  
• Step 6: Determining the value of cosec: (cosec x = 1/sin x)
  
• Step 7: Determining the value of sec: (sec x = 1/cos x)

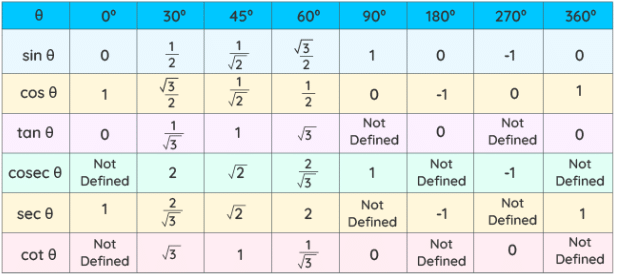
The following trigonometric table covers the value of trigonometric ratios for all basic angles ranging from 0º to 360º.

Trick to Remember Trigonometric Table

• Let us learn the one-hand trick for remembering the trigonometric table easily! Designate each finger the standard angles as shown in the image. For filling the sine values in the trigonometry table, we will include counting of the fingers, while for the cos table we will simply fill the values in reverse order.

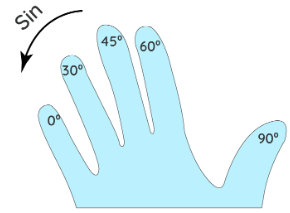
• Step 1: For the sine table, count the fingers on the left side for the standard angle.
• Step 2: Divide the number of fingers by 4
• Step 3: Take out the square root of the ratio.

Example 1: For sin 0°, there are no fingers on the left-hand side, therefore we will take 0. Dividing the zero by 4 we get 0. Taking the square root of the ratio we would get the value of sin 0° = 0
Example 2: For sin 60°, there are 3 fingers on the left-hand side. Dividing 3 by 4 we get (3/4). Taking the square root of the ratio √(3/4) we would get the value of sin 60° = √3/2.
Similarly, we can find out values for sin 30°, 45°, and 90° to fill the table.

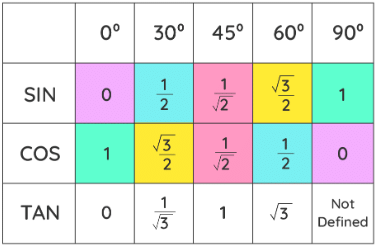
• In order to complete the cos table, simply fill in the values of sine in a reverse manner. For tan values, create the ratios by taking numerators of sine and cos values of the corresponding angle.
• Given below is a list of trigonometric formulas that would help you memorize the trigonometric table, based on the relationship between different trigonometric ratios.
  • sin x = cos (90° – x)
  • cos x = sin (90° – x)
  • tan x = cot (90° – x)
  • cot x = tan (90° – x)
  • sec x = cosec (90° – x)
  • cosec x = sec (90° – x)
  • 1/sin x = cosec x
  • 1/cos x = sec x
  • 1/tan x = cot x

Trigonometry Table in Radians

The trigonometric table for standard angles below presents the values of trigonometric ratios for the measure of angles given in radians.