Sectors, Areas, and Arcs | The Complete SAT Course - Class 10 PDF Download

Introduction

• As you may remember from geometry, the area A of a circle having a radius of length r is given:
  A = πr²
• The circumference C (that is, the length around the outside) of that same circle is given by:
  C  = 2πr
• These are the formulas give us the area and arc-length (that is, the length of the "arc", or curved line) for the entire circle. But sometimes we need to work with just a portion of a circle's revolution, or with many revolutions of the circle. What formulas do we use then?
• If we start with a circle with a marked radius line, and turn the circle a bit, the area marked off looks something like a wedge of pie or a slice of pizza; this is called a "sector" of the circle, and the sector looks like the green portion of this picture:

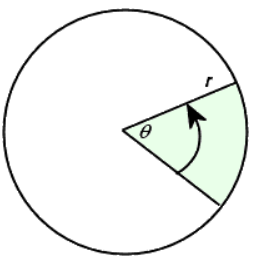
• The angle marked off by the original and final locations of the radius line (that is, the angle at the center of the pie / pizza) is the "subtended" angle of the sector. This angle can also be referred to as the "central" angle of the sector. In the picture above, the central angle is labelled as "θ" (which is pronounced as "THAY-tuh").

Affiliate

• What is the area A of the sector subtended by the marked central angle θ? What is the length s of the arc, being the portion of the circumference subtended by this angle?
• To determine these values, let's first take a closer look at the area and circumference formulas. The area and circumference are for the entire circle, one full revolution of the radius line. The subtended angle for "one full revolution" is 2π. So the formulas for the area and circumference of the whole circle can be restated as:
  
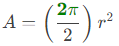
  C = (2π)r
• What is the point of splitting the angle value of "once around" the circle? I did this in order to highlight how the angle for the whole circle (being 2π) fits into the formulas for the whole circle. This then allows us to see exactly how and where the subtended angle θ of a sector will fit into the sector formulas. Now we can replace the "once around" angle (that is, the 2π) for an entire circle with the measure of a sector's subtended angle θ, and this will give us the formulas for the area and arc length of that sector:
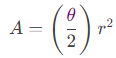  s = (θ) r

Note: If you are working with angles measured in degrees, instead of in radians, then you'll need to include an extra conversion factor: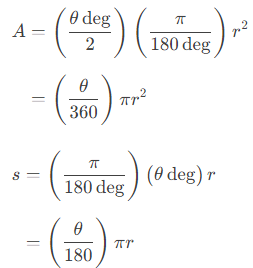

Confession: A big part of the reason that I've explained the relationship between the circle formulas and the sector formulas is that I could never keep track of the sector-area and arc-length formulas; I was always forgetting them or messing them up. But I could always remember the formulas for the area and circumference of an entire circle. So I learned (the hard way) that, by keeping the above relationship in mind, noting where the angles go in the whole-circle formulas, it is possible always to keep things straight.

Example

1. Given a circle with radius r = 8 units and a sector with subtended angle measuring 45°, find the area of the sector and the length of the arc.

They've given me the radius and the central angle, so I can just plug straight into the formulas, and simplify to get my answers. For convenience, I'll first convert "45°" to the corresponding radian value of  π/4. Then I'll do my plug-n-chug:

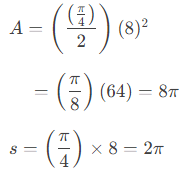
Then answer is:

area A = 8π square units, arc-length s = 2π units

• Notice how I put "units" on my answers. If they'd stated a specific unit for the radius, like "centimeters" or "miles" or whatever, then I could have been more specific in my answer. As it was, I had to be generic.
• Many times, if the question doesn't state a unit, or just says "units", then you can probably get away without putting "units" on your answer. However, this often leads to the bad habit of ignoring units entirely, and then — surprise! — the instructor counts off on the test because you didn't include any units. It's probably better to err on the side of caution, and always put some unit, even if it's just "units", on your answers.

2. Given a sector with radius r = 3 cm and a corresponding arc length of 5π radians, find the area of the sector.

• For this exercise, they've given me the radius and the arc length. To find the area of the sector, I need the measure of the central angle, which they did not give me. However, the formula for the arc length includes the central angle. So I can plug the radius and the arc length into the arc-length formula, and solve for the measure of the subtended angle. Once I've got that, I can plug-n-chug to find the sector area.
  
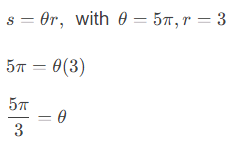
• So the central angle for this sector measures 5/3 π. Then the area of the sector is:
  
• And this value is the numerical portion of my answer. Since this value stands for "area", which is a square dimension, I'll want to remember to put "squared" on the units they gave me for the radius.
  A = 15π/2 cm²
• Sometimes, an exercise will give you information, but, like the above, it might not seem like it's the information that you actually need. Don't be afraid to fiddle with the values and the formulas; try to see if you can figure out a back door in to a solution, or some other manipulation that'll give you want you need. It's okay not to know, right at the beginning, how you're going to reach the end. (And, if they give you, or ask for, the diameter, remember that the radius is half of the diameter, and the diameter is twice the radius.)

3. A circle's sector has an area of 108 cm2, and the sector intercepts an arc with length 12 cm. Find the diameter of the circle.

• They've asked me for the diameter. The formulas I've learned use the radius. But I can find the radius, and then double it to get the diameter, so that's not a problem. However, they've asked me for a length, given the arc length and the area, each of which uses the radius and the subtended angle. And I have neither of those values. So what do I do?
• When I can't think of anything else to do, I plug whatever they've given me into whatever formulas might relate, and I hope something drops out of it that I can use. So:
  
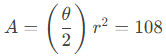
  s  = θr = 12
• I can substitute from the second line above into the first line above (after some rearrangement), and see if the result helps me at all:
  
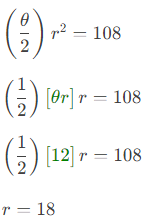
• I found the value for the radius! I don't have the value for the central angle, but they didn't ask for that, and it turns out that I didn't need it anyway. They asked me for the diameter, which is twice the radius, so my answer (including the units!) is:
  d = 36 cm