Engineering Mathematics Exam > Engineering Mathematics Notes > Engineering Mathematics > Relation & Its Types
Relation & Its Types | Engineering Mathematics - Engineering Mathematics PDF Download
Relations Definition
- A relation in mathematics defines the relationship between two different sets of information. If two sets are considered, the relation between them will be established if there is a connection between the elements of two or more non-empty sets.
- In the morning assembly at schools, students are supposed to stand in a queue in ascending order of the heights of all the students. This defines an ordered relation between the students and their heights.
- Therefore, we can say,
‘A set of ordered pairs is defined as a relation.’
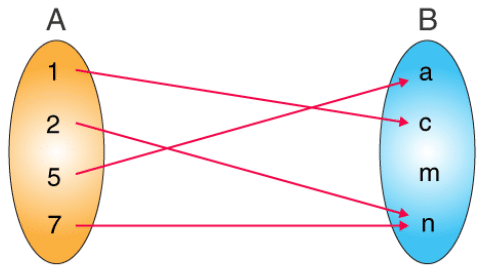
This mapping depicts a relation from set A into set B. A relation from A to B is a subset of A x B. The ordered pairs are (1,c),(2,n),(5,a),(7,n). For defining a relation, we use the notation where,
- set {1, 2, 5, 7} represents the domain.
- set {a, c, n} represents the range.
Sets and Relations
- Sets and relation are interconnected with each other. The relation defines the relation between two given sets.
- If there are two sets available, then to check if there is any connection between the two sets, we use relations.
- For example, an empty relation denotes none of the elements in the two sets is same.
Relations in Mathematics
- In Maths, the relation is the relationship between two or more set of values.
- Suppose, x and y are two sets of ordered pairs. And set x has relation with set y, then the values of set x are called domain whereas the values of set y are called range.
- Example: For ordered pairs={(1,2),(-3,4),(5,6),(-7,8),(9,2)}
- The domain is = {-7,-3,1,5,9}
- And range is = {2,4,6,8}
Types of Relations
There are 8 main types of relations which include:
1. Empty Relation
- An empty relation (or void relation) is one in which there is no relation between any elements of a set. For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relation,
R = φ ⊂ A × A
2. Universal Relation
- A universal (or full relation) is a type of relation in which every element of a set is related to each other. Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x – y| ≥ 0. For universal relation,
R = A × A
3. Identity Relation
- In an identity relation, every element of a set is related to itself only. For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,
I = {(a, a), a ∈ A}
4. Inverse Relation
- Inverse relation is seen when a set has elements which are inverse pairs of another set. For example if set A = {(a, b), (c, d)}, then inverse relation will be R-1 = {(b, a), (d, c)}. So, for an inverse relation,
R-1 = {(b, a): (a, b) ∈ R}
5. Reflexive Relation
- In a reflexive relation, every element maps to itself. For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-
(a, a) ∈ R
6. Symmetric Relation
- In a symmetric relation, if a=b is true then b=a is also true. In other words, a relation R is symmetric only if (b, a) ∈ R is true when (a,b) ∈ R. An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,
aRb ⇒ bRa, ∀ a, b ∈ A
7. Transitive Relation
- For transitive relation, if (x, y) ∈ R, (y, z) ∈ R, then (x, z) ∈ R. For a transitive relation,
aRb and bRc ⇒ aRc ∀ a, b, c ∈ A
8. Equivalence Relation
- If a relation is reflexive, symmetric and transitive at the same time, it is known as an equivalence relation.
The document Relation & Its Types | Engineering Mathematics - Engineering Mathematics is a part of the Engineering Mathematics Course Engineering Mathematics.
All you need of Engineering Mathematics at this link: Engineering Mathematics
|
65 videos|129 docs|94 tests
|
Related Searches





















