Group Theory | Engineering Mathematics - Civil Engineering (CE) PDF Download

Semigroup

A finite or infinite set ‘S′ with a binary operation ‘ο′ (Composition) is called semigroup if it holds following two conditions simultaneously −

• Closure − For every pair (a,b)∈S,(aοb) has to be present in the set S.
• Associative − For every element a,b,c∈S,(aοb)οc=aο(bοc) must hold.

Example

The set of positive integers (excluding zero) with addition operation is a semigroup. For example, S = {1,2,3,…}
Here closure property holds as for every pair (a,b)∈S,(a+b) is present in the set S. For example, 1+2=3∈S]
Associative property also holds for every element a,b,c∈S,(a+b)+c=a+(b+c). For example, (1+2)+3=1+(2+3)=5

Monoid

A monoid is a semigroup with an identity element. The identity element (denoted by e or E) of a set S is an element such that (aοe)=a, for every element a∈S. An identity element is also called a unit element. So, a monoid holds three properties simultaneously − Closure, Associative, Identity element.
Example
The set of positive integers (excluding zero) with multiplication operation is a monoid.
S={1,2,3,…}
Here closure property holds as for every pair (a,b)∈S,(a×b) is present in the set S.
[For example, 1×2=2∈S and so on]
Associative property also holds for every element a,b,c∈S,(a×b)×c=a×(b×c)
[For example, (1×2)×3=1×(2×3)=6 and so on]
Identity property also holds for every element a∈S,(a×e)=a
[For example, (2×1)=2,(3×1)=3 and so on]. Here identity element is 1.

Group

A group is a monoid with an inverse element. The inverse element (denoted by I) of a set S is an element such that (aοI)=(Iοa)=a, for each element a∈S. So, a group holds four properties simultaneously - i) Closure, ii) Associative, iii) Identity element, iv) Inverse element. The order of a group G is the number of elements in G and the order of an element in a group is the least positive integer n such that an is the identity element of that group G.

Examples
The set of N×N non-singular matrices form a group under matrix multiplication operation.
The product of two N×N non-singular matrices is also an N×N non-singular matrix which holds closure property.
Matrix multiplication itself is associative. Hence, associative property holds.
The set of N×N non-singular matrices contains the identity matrix holding the identity element property.
As all the matrices are non-singular they all have inverse elements which are also nonsingular matrices. Hence, inverse property also holds.

Clear all your Civil Engineering (CE) doubts with EduRev Join for Free

Join for Free

Abelian Group

An abelian group G is a group for which the element pair (a,b)∈G always holds commutative law. So, a group holds five properties simultaneously - i) Closure, ii) Associative, iii) Identity element, iv) Inverse element, v) Commutative.

Example
The set of positive integers (including zero) with addition operation is an abelian group.
G={0,1,2,3,…}
Here closure property holds as for every pair (a,b)∈S,(a+b) is present in the set S.
[For example, 1+2=2∈S and so on]
Associative property also holds for every element a,b,c∈S,(a+b)+c=a+(b+c)
[For example, (1+2)+3=1+(2+3)=6 and so on]
Identity property also holds for every element a∈S,(a×e)=a [For example, (2×1)=2,(3×1)=3 and so on]. Here, identity element is 1.
Commutative property also holds for every element a∈S,(a×b)=(b×a) [For example, (2×3)=(3×2)=3 and so on]

Cyclic Group and Subgroup

A cyclic group is a group that can be generated by a single element. Every element of a cyclic group is a power of some specific element which is called a generator. A cyclic group can be generated by a generator ‘g’, such that every other element of the group can be written as a power of the generator ‘g’.

Example
The set of complex numbers {1,−1,i,−i} under multiplication operation is a cyclic group.
There are two generators − i and –i as i¹=i, i²=−1, i³=−i, i⁴ = 1 and also (–i)¹=−i, (–i)²=−1, (–i)³=i,(–i)⁴=1 which covers all the elements of the group. Hence, it is a cyclic group.

Note: A cyclic group is always an abelian group but not every abelian group is a cyclic group. The rational numbers under addition is not cyclic but is abelian.
A subgroup H is a subset of a group G (denoted by H≤G) if it satisfies the four properties simultaneously − Closure, Associative, Identity element, and Inverse.
A subgroup H of a group G that does not include the whole group G is called a proper subgroup (Denoted by H<G). A subgroup of a cyclic group is cyclic and a abelian subgroup is also abelian.
Example
Let a group G={1,i,−1,−i}
Then some subgroups are H₁={1}, H₂={1,−1},

This is not a subgroup − H₃={1,i} because that (i)⁻¹=−i is not in H₃

Partially Ordered Set (POSET)

A partially ordered set consists of a set with a binary relation which is reflexive, antisymmetric and transitive. "Partially ordered set" is abbreviated as POSET.
Examples
The set of real numbers under binary operation less than or equal to (≤) is a poset.
Let the set S={1,2,3} and the operation is ≤
The relations will be {(1,1), (2,2), (3,3), (1,2), (1,3), (2,3)}

This relation R is reflexive as {(1,1), (2,2), (3,3)} ∈ R
This relation R is anti-symmetric, as
{(1,2), (1,3), (2,3)} ∈ R and {(1,2), (1,3), (2,3)} ∉ R
This relation R is also transitive as {(1,2), (2,3), (1,3)}∈R.
Hence, it is a poset.

The vertex set of a directed acyclic graph under the operation ‘reachability’ is a poset.

Download the notes Group Theory

Download as PDF

Download as PDF

Hasse Diagram

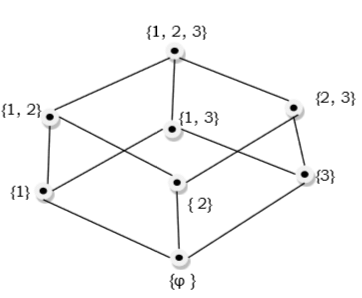
The Hasse diagram of a poset is the directed graph whose vertices are the element of that poset and the arcs covers the pairs (x, y) in the poset. If in the poset x<y, then the point x appears lower than the point y in the Hasse diagram. If x<y<z in the poset, then the arrow is not shown between x and z as it is implicit.

Example

The poset of subsets of {1,2,3}={∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}} is shown by the following Hasse diagram −

Linearly Ordered Set

A Linearly ordered set or Total ordered set is a partial order set in which every pair of element is comparable. The elements a, b ∈ S are said to be comparable if either a ≤ b or b ≤ a holds. Trichotomy law defines this total ordered set. A totally ordered set can be defined as a distributive lattice having the property {a∨b, a∧b}={a, b} for all values of a and b in set S.
Example
The powerset of {a,b} ordered by subseteq is a totally ordered set as all the elements of the power set P={∅,{a},{b},{a,b}} are comparable.
Example of non-total order set
A set S={1,2,3,4,5,6} under operation x divides y is not a total ordered set.
Here, for all (x,y)∈S, x|y have to hold but it is not true that 2 | 3, as 2 does not divide 3 or 3 does not divide 2. Hence, it is not a total ordered set.

Take a Practice Test Test yourself on topics from Civil Engineering (CE) exam

Practice Now

Practice Now

Lattice

A lattice is a poset (L,≤) for which every pair {a,b} ∈ L has a least upper bound (denoted by a∨b) and a greatest lower bound (denoted by a∧b). LUB ({a,b}) is called the join of a and b. GLB ({a,b}) is called the meet of a and b.

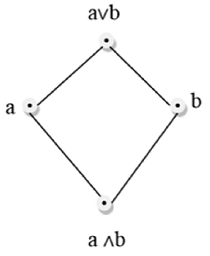
Example

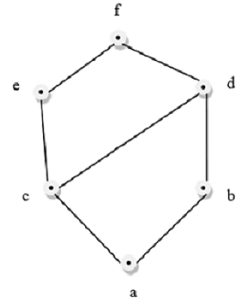
This above figure is a lattice because for every pair {a,b} ∈ L, a GLB and a LUB exists.

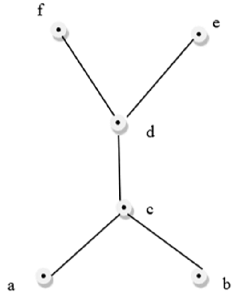
This above figure is a not a lattice because GLB(a,b) and LUB(e,f) does not exist.

Some other lattices are discussed below −

Bounded Lattice
A lattice L becomes a bounded lattice if it has a greatest element 1 and a least element 0.

Complemented Lattice
A lattice L becomes a complemented lattice if it is a bounded lattice and if every element in the lattice has a complement. An element x has a complement x’ if ∃x(x∧x′=0andx∨x′=1)

Distributive Lattice
If a lattice satisfies the following two distribute properties, it is called a distributive lattice.

• a∨(b∧c)=(a∨b)∧(a∨c)
• a∧(b∨c)=(a∧b)∨(a∧c)

Modular Lattice
If a lattice satisfies the following property, it is called modular lattice.
a∧(b∨(a∧d))=(a∧b)∨(a∧d)

Properties of Lattices

1. Idempotent Properties

• a∨a=a
• a∧a=a

2. Absorption Properties

• a∨(a∧b)=a
• a∧(a∨b)=a

3. Commutative Properties

• a∨b=b∨a
• a∧b=b∧a

4. Associative Properties

• a∨(b∨c)=(a∨b)∨c
• a∧(b∧c)=(a∧b)∧c

Dual of a Lattice
The dual of a lattice is obtained by interchanging the '∨' and '∧' operations.
Example
The dual of [a∨(b∧c)] is [a∧(b∨c)]