Havel's Hakimi Algorithm | Engineering Mathematics - Engineering Mathematics PDF Download
Introduction
In graph theory, the degree of a vertex is the number of connections it has. For example, the vertices of the below graph have degrees (3, 2, 2, 1).
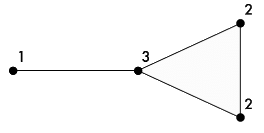
It is easy to determine the degrees of a graph’s vertices (i.e. its degree sequence), but what about the reverse problem? Given a list of integers, how can we construct a simple graph that has them as its vertex degrees? Does such a graph even exist? This blog post deals with a special case of this problem: constructing connected simple graphs with a given degree sequence using a simple and straightforward algorithm.
The Havel–Hakimi algorithm
If you are already familiar with this topic, feel free to skip ahead to the algorithm for building connected graphs.
Building a graph that realizes a certain degree sequence is usually done using the well-known Havel–Hakimi algorithm (HH). The algorithm can be understood most easily by imagining each vertex to have as many stubs as its degree. We then need to connect up all these stubs to form a graph.
For example, the degree sequence (3, 3, 2, 2, 1, 1) would be drawn like this:
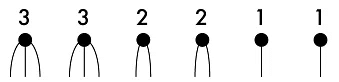 The numbers show how many unconnected stubs each vertex has.
The numbers show how many unconnected stubs each vertex has.
The HH algorithm proceeds by selecting an arbitrary vertex, and connecting up all of its stubs to the other vertices that have the most free stubs. This is repeated until no unconnected stubs are left. The procedure for the above degree sequence is illustrated below: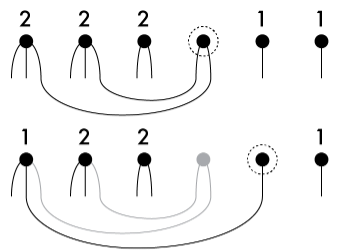
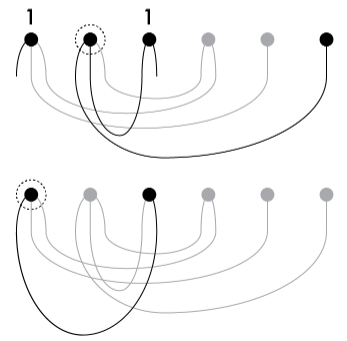
The vertex selected in each step is marked by the dotted circle. Some presentations of the HH algorithm, such as the one currently in Wikipedia, always select the vertex with the highest remaining degree. It is important to note that this is not necessary. Any vertex can be selected in each step, for as long as all of its stubs are connected up to the other vertices with the highest remaining degrees.
A degree sequence is said to be graphical if there exists a simple graph having it as its vertex degrees. The Havel–Hakimi theorem states that if the starting degree sequence is graphical, then the algorithm will succeed in connecting up all stubs without creating any self-loops.
A different formulation of the HH theorem is as follows:
Theorem: Let us order the degrees decreasingly with the exception of one vertex, and write the degree sequence as $d_1, \; d_2 \ge d_3 \ge \cdots \ge d_n$. This degree sequence is graphical if and only if $d_2 - 1, d_3 - 1, \ldots, d_{d_1 + 1} - 1, d_{d_1 + 2}, \ldots, d_n$ is also graphical.
In this view, a HH step takes a degree sequence, and reduces it to another, shorter one.
Building connected graphs
What if we are looking to build a connected graph with a given degree sequence? Not every degree sequence has a connected realization. Those that do are called potentially connected degree sequence.
The general Havel–Hakimi procedure does not always build connected graphs, even if the starting degree sequence was potentially connected. However, in each step of the algorithm, we have the freedom to select any vertex we like (and connect up all its stubs). It turns out that there is a special selection rule that guarantees that the result will be connected (provided that the starting degree sequence was potentially connected): always select the vertex with the smallest remaining degree. Let us refer to a HH step with this choice as a HH* step.
- Theorem: The smallest-first Havel–Hakimi algorithm (i.e. HH*) will produce a connected graph if and only if the starting degree sequence is potentially connected.
- Proof: The key to the proof is to show that if the starting degree sequence is potentially connected, then every HH* step reduces the number of vertices with non-zero remaining degree precisely by one. Reversing the order of the steps would then correspond to building a graph by adding one vertex at a time and connecting it to some existing vertices. This clearly results in a connected graph.
Let us think about what kind of degree sequence we need to start with in order for a HH* step to reduce the number of vertices by more than one. The selected vertex is always removed. Additional vertices will only be removed if they only had one remaining stub (i.e. they had degree 1), which was then connected up to the selected vertex. Since we always select a smallest-degree vertex, and connect it to other vertices with the highest degrees, this situation is only possible when both the smallest and largest degree is 1, i.e. the degree sequence contains only 1s. For example, the degree sequence $(1,1,1,1)$ is transformed to $(1,1)$ after one HH* step, i.e. it decreases in size by 2.
Except for $(1,1)$, such degree sequences are not potentially connected. Thus to show that the HH* algorithm never arrives to such a degree sequence, it is sufficient to show one HH* step transforms any potentially connected degree sequence to another potentially connected one. We invoke the following lemma: - Lemma: A degree sequence $d_i, i=1..n$ is potentially connected if and only if $d_i \ge 1, \forall i$ and $\sum_{i=1}^n d_i \ge 2(n-1)$ (in other words, the number of edges is at least $n-1$).
[This can be shown by recalling that trees (i.e. cycle-free connected graphs) have precisely $n-1$ edges. Thus one component of a non-connected graph with at least $n-1$ edges must have a cycle, and there exists a degree-sequence-preserving edge swap that will connect it to another component.]
After one HH* step, the right-hand-side of this inequality becomes $2(n-2) = 2(n-1)-2$, i.e. decreases by 2. What about left-hand-side?
If the selected vertex had degree 1, then the left-hand-side also decreases by 2, thus the inequality is maintained.
If the selected smallest-degree vertex had degree $k\ge2$, then the sum of degrees is at least $nk$, $\sum_{i=1}^n d_i \ge nk$. After one HH* step, the sum of degrees decreases by $2k$, thus we only need to show that $nk - 2k \ge 2(n-2)$, which is obviously true for $k \ge 2$. The inequality is maintained again. $\blacksquare$
Conclusion
- Realizing degree sequences as connected graphs is sometimes done by first building an arbitrary (not necessarily connected) realization, then merging the components with appropriate degree-sequence-preserving edge swaps (see e.g. Viger & Latapy). This method is complicated and difficult to program. The smallest-first version of Havel–Hakimi algorithm that I offer here is a much simpler procedure to obtain a connected graph. I was unable to find a previsouly published version of this method for building connected graphs from a degree sequence, so I decided to share it through this blog post. If you are aware of a prior decription of this algorithm, please let me know.
- An implementation of this algorithm is available in the IGraph/M Mathematica package as the IGRealizeDegreeSequence function’s default "SmallestFirst" method, and eventually in the core igraph library as well.
As a demonstration, let us produce an arbitrary potentially connected degree sequence:
In[]= degseq = VertexDegree@First@ConnectedGraphComponents@RandomGraph[{50, 50}]
Out[]= {2, 3, 5, 3, 2, 3, 4, 4, 3, 4, 2, 1, 5, 3, 2, 2, 2, 4, 2, 6, 3, 2, 2, \
1, 1, 2, 2, 2, 2, 2, 3, 1, 1, 1, 1}
The usual largest-first implementation of the Havel–Hakimi algorithm typically produces disconnected graphs:
IGRealizeDegreeSequence[degseq, Method -> "LargestFirst"]
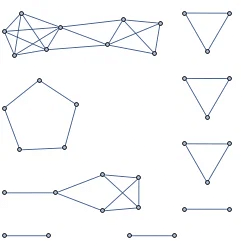
The default method of the IGRealizeDegreeSequence function (Method -> "SmallestFirst") guarantees a connected realization, if one exists.
IGRealizeDegreeSequence[degseq]
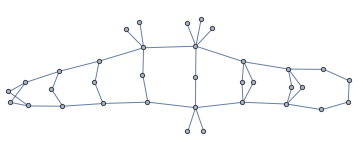
|
65 videos|129 docs|94 tests
|
















