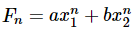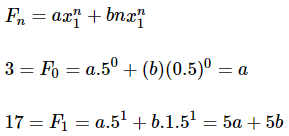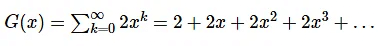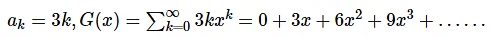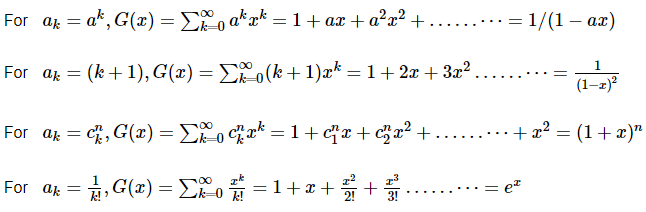Recurrence Relations | Engineering Mathematics - Civil Engineering (CE) PDF Download

Clear all your Civil Engineering (CE) doubts with EduRev Join for Free

Join for Free

Introduction

A recurrence relation is an equation that recursively defines a sequence where the next term is a function of the previous terms (Expressing F_n as some combination of F_i with i < n).
Example − Fibonacci series − F_n = F_n−1 + F_n−2, Tower of Hanoi − F_n = 2F_n−1 + 1

Linear Recurrence Relations

A linear recurrence equation of degree k or order k is a recurrence equation which is in the format x_n = A₁x_n−1 + A₂x_n−1 + A₃x_n−1 +…A_kx_n−k (A_n is a constant and A_k ≠ 0) on a sequence of numbers as a first-degree polynomial.
These are some examples of linear recurrence equations −

How to solve linear recurrence relation

Suppose, a two ordered linear recurrence relation is − F_n = AF_n−1 + BF_n−2 where A and B are real numbers.
The characteristic equation for the above recurrence relation is −
x² − Ax − B = 0

Three cases may occur while finding the roots −

• Case 1 − If this equation factors as (x − x₁)(x − x₁) = 0 and it produces two distinct real roots x₁ and x₂, then F_n = 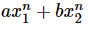 is the solution. [Here, a and b are constants]
• Case 2 − If this equation factors as (x - x₁)² = 0 and it produces single real root x₁, then F_n = 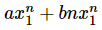 is the solution.
• Case 3 − If the equation produces two distinct complex roots, x₁ and x₂ in polar form x₁ = r ∠ θ and x₂ = r∠(−θ), then F_n = rⁿ(acos(nθ) + bsin(nθ)) is the solution.

Problem 1: Solve the recurrence relation F_n = 5F_n−1 − 6F_n−2 where F₀ = 1 and F₁ = 4

The characteristic equation of the recurrence relation is −

x² − 5x + 6 = 0,
So, (x−3)(x−2)=0
Hence, the roots are −
x₁ = 3 and x₂ = 2
The roots are real and distinct. So, this is in the form of case 1
Hence, the solution is −

Here, F_n = a3ⁿ + b2ⁿ (As x₁ = 3 and x₂ = 2)

Therefore,
1 = F₀ = a3⁰ + b2⁰ = a + b
4 = F₁ = a3¹ + b2¹ = 3a + 2b

Solving these two equations, we get a = 2 and b = −1
Hence, the final solution is −
F_n = 2.3ⁿ + (−1).2ⁿ = 2.3ⁿ − 2ⁿ

Problem 2: Solve the recurrence relation − F_n = 10F_n−1−25F_n−2 where F₀ = 3 and F₁ = 17

The characteristic equation of the recurrence relation is −
x² − 10x − 25 = 0
So (x−5)² = 0

Hence, there is single real root x₁ = 5
As there is single real valued root, this is in the form of case 2
Hence, the solution is −

Solving these two equations, we get a = 3 and b = 2/5
Hence, the final solution is − F_n = 3.5ⁿ + (2/5).n.2ⁿ

Problem 3: Solve the recurrence relation F_n = 2F_n−1−2F_n−2 where F₀ = 1 and F₁ = 3

The characteristic equation of the recurrence relation is −
x² − 2x − 2 = 0

Hence, the roots are −
x₁ = 1 + i and x₂ = 1 − i
In polar form,
x₁ = r∠θ and x₂ = r∠(−θ), where r = √2 and θ = π/4
The roots are imaginary. So, this is in the form of case 3.
Hence, the solution is −
F_n = (2–√)ⁿ(acos(n.⊓/4) + bsin(n.⊓/4))

1 = F₀ = (2–√)⁰(acos(0.⊓/4)+bsin(0.⊓/4)) = a

3 = F₁ = (2–√)¹(acos(1.⊓/4) + bsin(1.⊓/4)) = 2–√(a/2–√ + b/2–√)

Solving these two equations we get a=1 and b=2

Hence, the final solution is −
Fn = (√2)n(cos(n.π/4)+2sin(n.π/4))

Non-Homogeneous Recurrence Relation and Particular Solutions

A recurrence relation is called non-homogeneous if it is in the form
F_n = AF_n−1 + BF_n−2 + f(n) where f(n) ≠ 0

Its associated homogeneous recurrence relation is F_n = AF_n–1 + BF_n−2

The solution (a_n) of a non-homogeneous recurrence relation has two parts.
First part is the solution (a_h) of the associated homogeneous recurrence relation and the second part is the particular solution (a_t).
a_n = a_h + a_t

Solution to the first part is done using the procedures discussed in the previous section.
To find the particular solution, we find an appropriate trial solution.
Let f(n) = cxⁿ ; let x² = Ax+B be the characteristic equation of the associated homogeneous recurrence relation and let x₁ and x₂ be its roots.
If x ≠ x₁ and x ≠ x₂, then at = Axⁿ
If x = x₁, x ≠ x₂, then at = Anxⁿ
If x = x₁ = x₂, then at = An²xⁿ

Example

Let a non-homogeneous recurrence relation be F_n =  AF_n–1 + BF_n−2 +  f(n) with characteristic roots x₁ = 2 and x₂ = 5. Trial solutions for different possible values of f(n) are as follows −

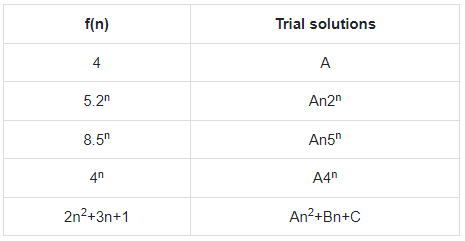
Problem: Solve the recurrence relation F_n = 3F_n−1 + 10F_n−2 + 7.5ⁿ where F₀ = 4 and F₁ = 3

This is a linear non-homogeneous relation, where the associated homogeneous equation is F_n = 3F_n−1 + 10F_n−2 and f(n) = 7.5ⁿ
The characteristic equation of its associated homogeneous relation is −
x² − 3x − 10 = 0
Or, (x − 5)(x + 2) = 0
Or, x₁ = 5 and x₂ = −2
Hence a_h = a.5ⁿ + b.(−2)ⁿ , where a and b are constants.
Since f(n) = 7.5ⁿ, i.e. of the form c.xⁿ, a reasonable trial solution of at will be Anxⁿ
at = Anx_n = An5ⁿ
After putting the solution in the recurrence relation, we get −
An5ⁿ = 3A(n–1)5ⁿ⁻¹ + 10A(n–2)5ⁿ⁻² + 7.5ⁿ

Dividing both sides by 5ⁿ⁻², we get
An5² = 3A(n−1)5 + 10A(n−2)5⁰ + 7.52

Or, 25An = 15An − 15A + 10An − 20A + 175
Or, 35A = 175
Or, A = 5
So, F_n = An5ⁿ = 5n5ⁿ = n5ⁿ⁺¹
The solution of the recurrence relation can be written as −
F_n = a_h + a_t
= a.5ⁿ + b.(−2)ⁿ + n5^{n + 1}

Putting values of F₀ = 4 and F₁ = 3, in the above equation, we get a = −2 and b = 6
Hence, the solution is −
Fn = n5ⁿ⁺¹ + 6.(−2)ⁿ⁻².5n

Generating Functions

Generating Functions represents sequences where each term of a sequence is expressed as a coefficient of a variable x in a formal power series.
Mathematically, for an infinite sequence, say a₀, a₁, a₂,…,ak,…, the generating function will be −

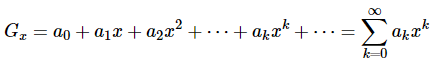
Some Areas of Application

Generating functions can be used for the following purposes −

• For solving a variety of counting problems. For example, the number of ways to make change for a Rs. 100 note with the notes of denominations Rs.1, Rs.2, Rs.5, Rs.10, Rs.20 and Rs.50
• For solving recurrence relations
• For proving some of the combinatorial identities
• For finding asymptotic formulae for terms of sequences

Problem 1:  What are the generating functions for the sequences {a_k} with a_k = 2 and a_k = 3k?

When a_k = 2, generating function,  

When

Problem 2: What is the generating function of the infinite series; 1,1,1,1,…?

Here, a_k = 1, for 0 ≤ k ≤ ∞
Hence, G(x) = 1 + x + x₂ + x₃ +…⋯ = 1/(1−x)

Some Useful Generating Functions

For ak=ak,G(x)=∑∞k=0akxk=1+ax+a2x2+……⋯=1/(1−ax)

For ak=(k+1),G(x)=∑∞k=0(k+1)xk=1+2x+3x2……⋯=1(1−x)2

For ak=cnk,G(x)=∑∞k=0cnkxk=1+cn1x+cn2x2+……⋯+x2=(1+x)n

For ak=1k!,G(x)=∑∞k=0xkk!=1+x+x22!+x33!……⋯=ex