Integer Representation | Digital Logic - Computer Science Engineering (CSE) PDF Download

Integers are whole numbers or fixed-point numbers with the radix point fixed after the least-significant bit. They are contrast to real numbers or floating-point numbers, where the position of the radix point varies. It is important to take note that integers and floating-point numbers are treated differently in computers. They have different representation and are processed differently (e.g., floating-point numbers are processed in a so-called floating-point processor). Floating-point numbers will be discussed later.
Computers use a fixed number of bits to represent an integer. The commonly-used bit-lengths for integers are 8-bit, 16-bit, 32-bit or 64-bit. Besides bit-lengths, there are two representation schemes for integers:

• Unsigned Integers: can represent zero and positive integers.
• Signed Integers: can represent zero, positive and negative integers. Three representation schemes had been proposed for signed integers:
  • Sign-Magnitude representation
  • 1's Complement representation
  • 2's Complement representation

You, as the programmer, need to decide on the bit-length and representation scheme for your integers, depending on your application's requirements. Suppose that you need a counter for counting a small quantity from 0 up to 200, you might choose the 8-bit unsigned integer scheme as there is no negative numbers involved.

n-bit Unsigned Integers

Example 1: Suppose that n = 8 and the binary pattern is 0100 0001B, the value of this unsigned integer is 1×2⁰ + 1×2⁶ = 65D.

Example 2: Suppose that n=16 and the binary pattern is 0001 0000 0000 1000B, the value of this unsigned integer is 1×2³ + 1×2¹² = 4104D.

Example 3: Suppose that n=16 and the binary pattern is 0000 0000 0000 0000B, the value of this unsigned integer is 0.

An n-bit pattern can represent 2ⁿ distinct integers. An n-bit unsigned integer can represent integers from 0 to (2ⁿ)-1, as tabulated below:

Signed Integers

• Sign-Magnitude representation
• 1's Complement representation
• 2's Complement representation

In all the above three schemes, the most-significant bit (msb) is called the sign bit. The sign bit is used to represent the sign of the integer - with 0 for positive integers and 1 for negative integers. The magnitude of the integer, however, is interpreted differently in different schemes.

n-bit Sign Integers in Sign-Magnitude Representation

In sign-magnitude representation:

• The most-significant bit (msb) is the sign bit, with value of 0 representing positive integer and 1 representing negative integer.
• The remaining n-1 bits represents the magnitude (absolute value) of the integer. The absolute value of the integer is interpreted as "the magnitude of the (n-1)-bit binary pattern".

Example 1: Suppose that n=8 and the binary representation is 0 100 0001B.
Sign bit is 0 ⇒ positive
Absolute value is 100 0001B = 65D
Hence, the integer is +65D

Example 2: Suppose that n=8 and the binary representation is 1 000 0001B.
Sign bit is 1 ⇒ negative
Absolute value is 000 0001B = 1D
Hence, the integer is -1D

Example 3: Suppose that n=8 and the binary representation is 0 000 0000B.
Sign bit is 0 ⇒ positive
Absolute value is 000 0000B = 0D
Hence, the integer is +0D

Example 4: Suppose that n=8 and the binary representation is 1 000 0000B.
Sign bit is 1 ⇒ negative
Absolute value is 000 0000B = 0D
Hence, the integer is -0D

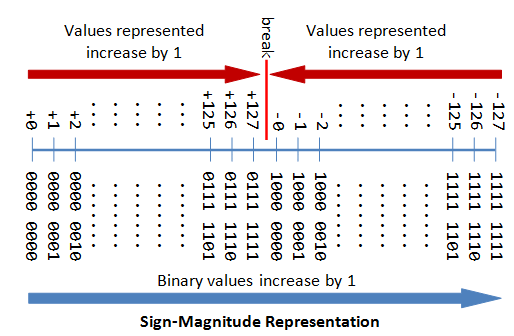
The drawbacks of sign-magnitude representation are:

• There are two representations (0000 0000B and 1000 0000B) for the number zero, which could lead to inefficiency and confusion.
• Positive and negative integers need to be processed separately.

n-bit Sign Integers in 1's Complement Representation

• Again, the most significant bit (msb) is the sign bit, with value of 0 representing positive integers and 1 representing negative integers.
• The remaining n-1 bits represents the magnitude of the integer, as follows:
  • for positive integers, the absolute value of the integer is equal to "the magnitude of the (n-1)-bit binary pattern".
  • for negative integers, the absolute value of the integer is equal to "the magnitude of the complement (inverse) of the (n-1)-bit binary pattern" (hence called 1's complement).

Example 1: Suppose that n=8 and the binary representation 0 100 0001B.
Sign bit is 0 ⇒ positive
Absolute value is 100 0001B = 65D
Hence, the integer is +65D

Example 2: Suppose that n=8 and the binary representation 1 000 0001B.
Sign bit is 1 ⇒ negative
Absolute value is the complement of 000 0001B, i.e., 111 1110B = 126D
Hence, the integer is -126D

Example 3: Suppose that n=8 and the binary representation 0 000 0000B.
Sign bit is 0 ⇒ positive
Absolute value is 000 0000B = 0D
Hence, the integer is +0D

Example 4: Suppose that n=8 and the binary representation 1 111 1111B.
Sign bit is 1 ⇒ negative
Absolute value is the complement of 111 1111B, i.e., 000 0000B = 0D
Hence, the integer is -0D

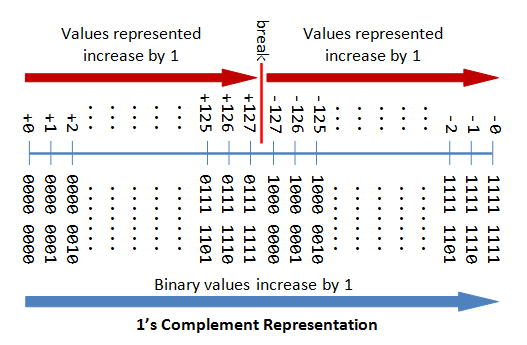
Again, the drawbacks are:

• There are two representations (0000 0000B and 1111 1111B) for zero.
• The positive integers and negative integers need to be processed separately.

n-bit Sign Integers in 2's Complement Representation

In 2's complement representation:

• Again, the most significant bit (msb) is the sign bit, with value of 0 representing positive integers and 1 representing negative integers.
• The remaining n-1 bits represents the magnitude of the integer, as follows:
  • for positive integers, the absolute value of the integer is equal to "the magnitude of the (n-1)-bit binary pattern".
  • for negative integers, the absolute value of the integer is equal to "the magnitude of the complement of the (n-1)-bit binary pattern plus one" (hence called 2's complement).

Example 1: Suppose that n=8 and the binary representation 0 100 0001B.
Sign bit is 0 ⇒ positive
Absolute value is 100 0001B = 65D
Hence, the integer is +65D

Example 2: Suppose that n=8 and the binary representation 1 000 0001B.
Sign bit is 1 ⇒ negative
Absolute value is the complement of 000 0001B plus 1, i.e., 111 1110B + 1B = 127D
Hence, the integer is -127D

Example 3: Suppose that n=8 and the binary representation 0 000 0000B.
Sign bit is 0 ⇒ positive
Absolute value is 000 0000B = 0D
Hence, the integer is +0D

Example 4: Suppose that n=8 and the binary representation 1 111 1111B.
Sign bit is 1 ⇒ negative
Absolute value is the complement of 111 1111B plus 1, i.e., 000 0000B + 1B = 1D
Hence, the integer is -1D

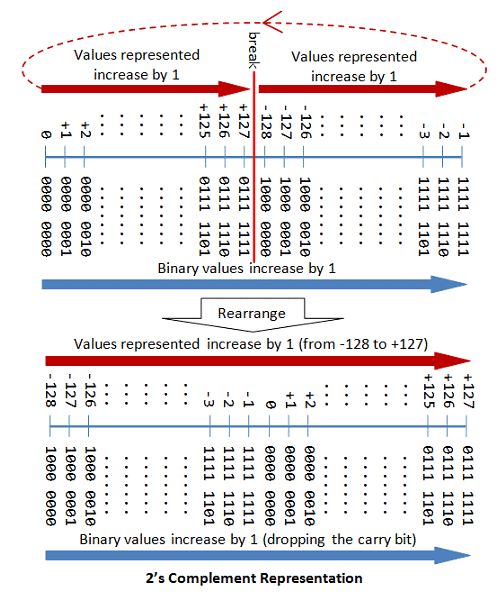
Computers use 2's Complement Representation for Signed Integers

We have discussed three representations for signed integers: signed-magnitude, 1's complement and 2's complement. Computers use 2's complement in representing signed integers. This is because:

• There is only one representation for the number zero in 2's complement, instead of two representations in sign-magnitude and 1's complement.
• Positive and negative integers can be treated together in addition and subtraction. Subtraction can be carried out using the "addition logic".

Example 1: Addition of Two Positive Integers: Suppose that n=8, 65D + 5D = 70D

65D →    0100 0001B

5D →    0000 0101B(+
0100 0110B    → 70D (OK)

Example 2: Subtraction is treated as Addition of a Positive and a Negative Integers: Suppose that n=8, 5D - 5D = 65D + (-5D) = 60D

65D →    0100 0001B

-5D →    1111 1011B(+

0011 1100B    → 60D (discard carry - OK)

Example 3: Addition of Two Negative Integers: Suppose that n=8, -65D - 5D = (-65D) + (-5D) = -70D

-65D →    1011 1111B

-5D →    1111 1011B(+

1011 1010B    → -70D (discard carry - OK)

Because of the fixed precision (i.e., fixed number of bits), an n-bit 2's complement signed integer has a certain range. For example, for n=8, the range of 2's complement signed integers is -128 to +127. During addition (and subtraction), it is important to check whether the result exceeds this range, in other words, whether overflow or underflow has occurred.

Example 4: Overflow: Suppose that n=8, 127D + 2D = 129D (overflow - beyond the range)

127D →    0111 1111B

 2D →    0000 0010B(+

1000 0001B    → -127D (wrong)

Example 5: Underflow: Suppose that n=8, -125D - 5D = -130D (underflow - below the range)

-125D →    1000 0011B

-5D →    1111 1011B(+

0111 1110B    → +126D (wrong)

The following diagram explains how the 2's complement works. By re-arranging the number line, values from -128 to +127 are represented contiguously by ignoring the carry bit.

Range of n-bit 2's Complement Signed Integers

An n-bit 2's complement signed integer can represent integers from -2^(n-1) to +2^(n-1)-1, as tabulated. Take note that the scheme can represent all the integers within the range, without any gap. In other words, there is no missing integers within the supported range.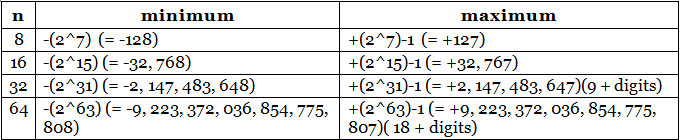

Decoding 2's Complement Numbers

• Check the sign bit (denoted as S).
• If S = 0, the number is positive and its absolute value is the binary value of the remaining n-1 bits.
• If S = 1, the number is negative. you could "invert the n-1 bits and plus 1" to get the absolute value of negative number.
  Alternatively, you could scan the remaining n-1 bits from the right (least-significant bit). Look for the first occurrence of 1. Flip all the bits to the left of that first occurrence of 1. The flipped pattern gives the absolute value. For example,

n = 8, bit pattern = 1 100 0100B

S = 1 → negative
Scanning from the right and flip all the bits to the left of the first occurrence of 1 ⇒ 011 1100B = 60D
Hence, the value is -60D

Big Endian vs. Little Endian

• Modern computers store one byte of data in each memory address or location, i.e., byte addressable memory. An 32-bit integer is, therefore, stored in 4 memory addresses.
• The term"Endian" refers to the order of storing bytes in computer memory. In "Big Endian" scheme, the most significant byte is stored first in the lowest memory address (or big in first), while "Little Endian" stores the least significant bytes in the lowest memory address.
• For example, the 32-bit integer 12345678H (30541989610) is stored as 12H 34H 56H 78H in big endian; and 78H 56H 34H 12H in little endian. An 16-bit integer 00H 01H is interpreted as 0001H in big endian, and 0100H as little endian.

Exercise (Integer Representation)

• What are the ranges of 8-bit, 16-bit, 32-bit and 64-bit integer, in "unsigned" and "signed" representation?

The range of unsigned n-bit integers is [0, 2^n - 1]. The range of n-bit 2's complement signed integer is [-2^(n-1), +2^(n-1)-1];

• Give the value of 88, 0, 1, 127, and 255 in 8-bit unsigned representation.

88 (0101 1000), 0 (0000 0000), 1 (0000 0001), 127 (0111 1111), 255 (1111 1111).

• Give the value of +88, -88 , -1, 0, +1, -128, and +127 in 8-bit 2's complement signed representation.

+88 (0101 1000), -88 (1010 1000), -1 (1111 1111), 0 (0000 0000), +1 (0000 0001), -128 (1000 0000), +127 (0111 1111).

• Give the value of +88, -88 , -1, 0, +1, -127, and +127 in 8-bit sign-magnitude representation.

+88 (0101 1000), -88 (1101 1000), -1 (1000 0001), 0 (0000 0000 or 1000 0000), +1 (0000 0001), -127 (1111 1111), +127 (0111 1111).

• Give the value of +88, -88 , -1, 0, +1, -127 and +127 in 8-bit 1's complement representation.

+88 (0101 1000), -88 (1010 0111), -1 (1111 1110), 0 (0000 0000 or 1111 1111), +1 (0000 0001), -127 (1000 0000), +127 (0111 1111).