Cheatsheet: Speed Time & Distance | General Aptitude for GATE - Mechanical Engineering PDF Download

Theory

The questions in this section can vary from being very easy to surprisingly difficult. This is a conceptual section and some of the questions can consume a lot of time. While solving, write down the equations as far as possible to avoid mistakes. The few extra seconds can help you avoid silly mistakes. Also, check if the units of distance, speed and time match up. So if you see yourself adding a unit of distance like m to a unit of speed m/s, you would realize you have missed a term. Choose to apply the concept of relative speed wherever possible as it can greatly reduce the complexity of the problem. Like speed and distance, in time and work while working with terms ensure that you convert all terms to consistent units like man-hours.

Formula

(i) Two objects travel the same distance (D) with different spee ds of S₁ and S₂. If the difference between the journey times is t then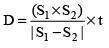

(ii) If an object travels a distance of D with a speed of S₁ and returns with a speed of S₂ taking a total time of 't', then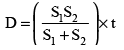

(iii) If two objects travel the same distance with speeds of S₁ and S₂ taking the journey times of t₁ and t₂ respectively, then S₁: S₂ = t₂ : t₁ OR  t₁ : t₂ = S₂ : S₁ 
(iv) Walking at p/qth of usual speed a man reaches his destination t-hours late (or early) then usual time to reach the office is given by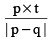
(v) If a person walks a distance D with a speed of S₁ kmph then he will be late (early) by t₁ hours. If he walks at S₂ kmph he will be late (early) by t₂ hours. Then the distance travelled by the person is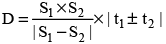
Note: Use (+) sign if the person is late in one case and early in the other case. Use (-) sign if he is late in both the cases or early in both the cases.
(vi) If an object travels different distances with different speeds during a journey then the entire journey can be represented by a single equivalent speed called Average Speed (S_A)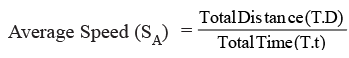

(vii) If an object travels a distance of D₁–km with S₁–kmph another D₂–km with a speed of S₂-kmph and D₃-km with a speed of S₃-kmph, then the average speed of the journey is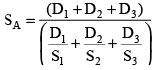

(viii) If an object travels with a speed of S₁-kmph for t₁-hours, next wi-th a speed of S₂ kmph for t₂-hours and with a speed of S₃-kmph for t₃–hours, then the average speed (S_A) for the whole journey is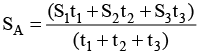

Tips

• In a journey travelled with different speeds, if the distance covered in each stage is constant, the average speed is the harmonic mean of the different speeds.
• In a journey travelled with different speeds, if the time travelled in each stage is constant, the average speed is the arithmetic mean of the different speeds.

Solved Example