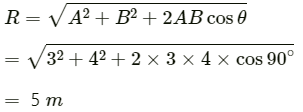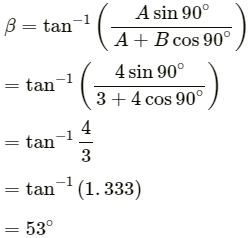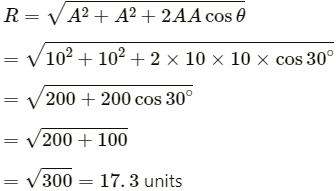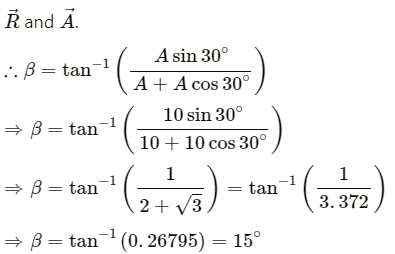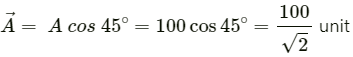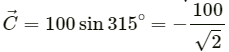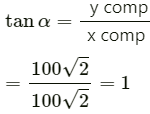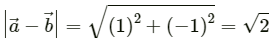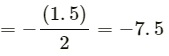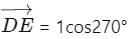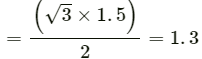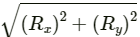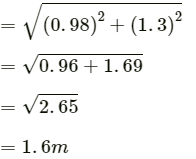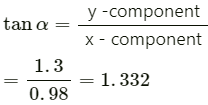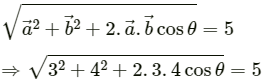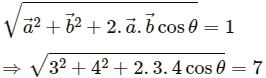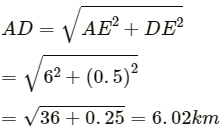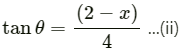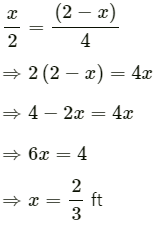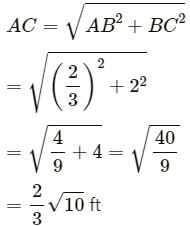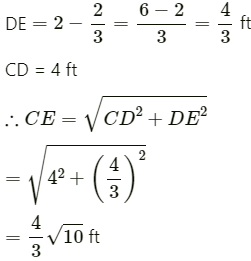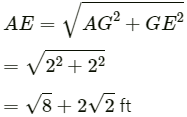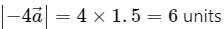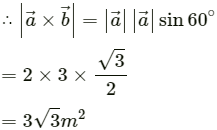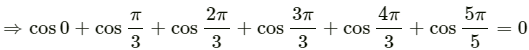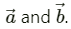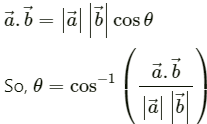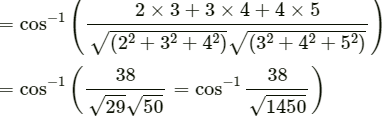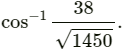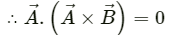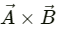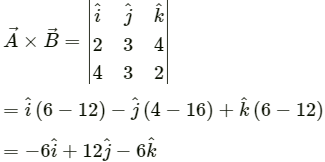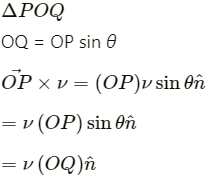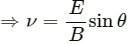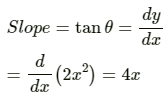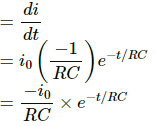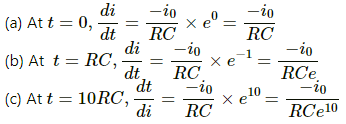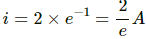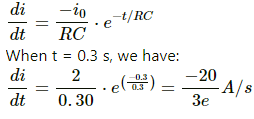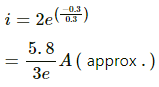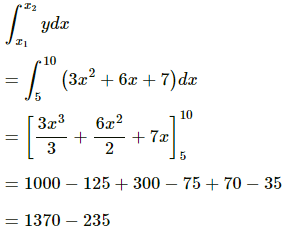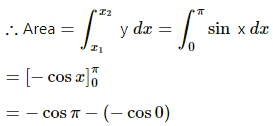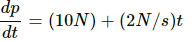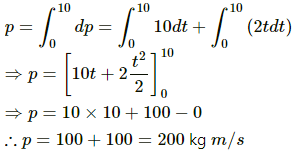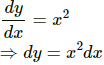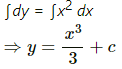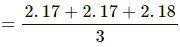HC Verma Questions and Solutions: Chapter 2- Physics & Mathematics- 2 | HC Verma Solutions - JEE PDF Download
Exercise
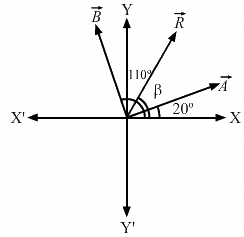
Q.1. A vector 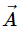 makes an angle of 20° and
makes an angle of 20° and  makes an angle of 110° with the X-axis. The magnitudes of these vectors are 3 m and 4 m respectively. Find the resultant.
makes an angle of 110° with the X-axis. The magnitudes of these vectors are 3 m and 4 m respectively. Find the resultant.
From the above figure, we have:
Angle between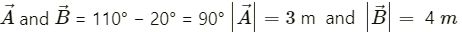
Magnitude of the resultant vector is given by
Let β be the angle between
Now, angle made by the resultant vector with the X-axis = 53° + 20° = 73°
∴ The resultantis 5 m and it makes an angle of 73° with the x-axis.
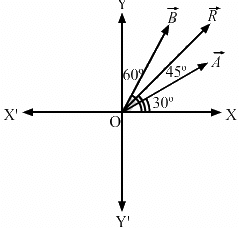
Q.2. Let 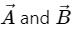 be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angle 30° and 60° respectively, find the resultant.
be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angle 30° and 60° respectively, find the resultant.
Angle between
θ = 60° − 30° = 30°
units
The magnitude of the resultant vector is given by
Let β be the angle between
Angle made by the resultant vector with the X-axis = 15° + 30° = 45°
∴ The magnitude of the resultant vector is 17.3 and it makes angle of 45° with the X-axis.
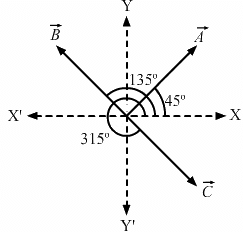
Q.3. Add vectors 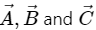 each having magnitude of 100 unit and inclined to the X-axis at angles 45°, 135° and 315° respectively.
each having magnitude of 100 unit and inclined to the X-axis at angles 45°, 135° and 315° respectively.
First, we will find the components of the vector along the x-axis and y-axis. Then we will find the resultant x and y-components.
x-component of
x-component of
x-component ofcos 315°
= 100 cos 315°
Resultant x-component =
Now, y-component of
y-component of
y-component of
Resultant y-component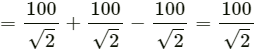
Magnitude of the resultant =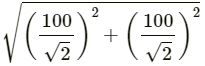
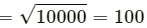
Angle made by the resultant vector with the x-axis is given by
⇒ α = tan−1 (1) = 45°
∴ The magnitude of the resultant vector is 100 units and it makes an angle of 45° with the x-axis.
Q.4. Let 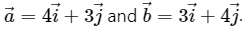 Find the magnitudes of (a)
Find the magnitudes of (a) 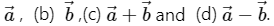
Given:
(a) Magnitude ofis given by
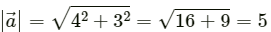
Magnitude ofis given by
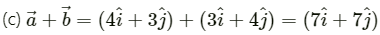
∴ Magnitude of vectoris given by
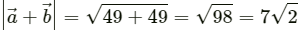
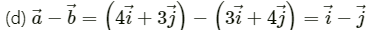
∴ Magnitude of vectoris given by
Q.5. Refer to figure (2-E1). Find (a) the magnitude, (b) x and y component and (c) the angle with the X-axis of the resultant of 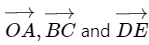
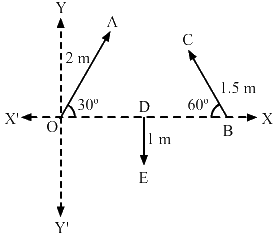
First, let us find the components of the vectors along the x and y-axes. Then we will find the resultant x and y-components.
x-component of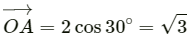
x-component of= 1.5cos120°
x-component of
= 1 × 0 = 0 m
y-component of= 2 sin 30° = 1
y-component of= 1.5 sin 120°
y-component of= 1 sin 270° = −1
x-component of resultant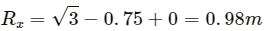
y-component of resultant Ry = 1 + 1.3 − 1 = 1.3 m
∴ Resultant, R =
If it makes an angle α with the positive x-axis, then
∴ α = tan−1 (1.32).
Q.6. Two vectors have magnitudes 2 unit and 4 unit respectively. What should be the angle between them if the magnitude of the resultant is (a) 1 unit, (b) 5 unit and (c) 7 unit.
Let the two vectors be
Now,
(a) If the resultant vector is 1 unit, then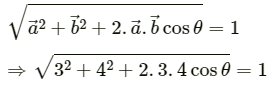
Squaring both sides, we get:
Hence, the angle between them is 180°.
(b) If the resultant vector is 5 units, then
Squaring both sides, we get:
25 + 24 cos θ = 25
⇒ 24 cos θ = 0
⇒ cos θ = 90°
Hence, the angle between them is 90°.
(c) If the resultant vector is 7 units, then
Squaring both sides, we get:
25 + 24 cos θ = 49,
⇒ 24 cos θ = 24
⇒ cos θ = 1
⇒ θ = cos−1 1 = 0°
Hence, the angle between them is 0°.
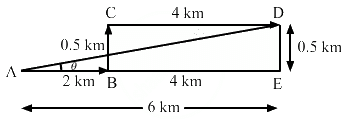
Q.7. A spy report about a suspected car reads as follows. "The car moved 2.00 km towards east, made a perpendicular left turn, ran for 500 m, made a perpendicular right turn, ran for 4.00 km and stopped". Find the displacement of the car.
The displacement of the car is represented by
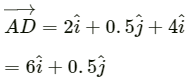
Magnitude ofis given by
Now,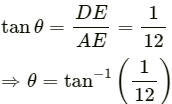
Hence, the displacement of the car is 6.02 km along the directionwith positive the x-axis.
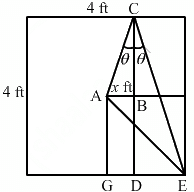
Q.8. A carrom board (4 ft × 4 ft square) has the queen at the centre. The queen, hit by the striker moves to the from edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen (a) from the centre to the front edge, (b) from the front edge to the hole and (c) from the centre to the hole.
Consider that the queen is initially at point A as shown in the figure.
Let AB be x ft.
So, DE = (2 − x) ft
In ∆ABC, we have: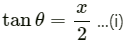
Also, in ∆DCE, we have:
From (i) and (ii), we get:
(a) In ∆ABC, we have:
(b) In ∆CDE, we have:
(c) In ∆AGE, we have:
Q.9. A mosquito net over a 7 ft × 4 ft bed is 3 ft high. The net has a hole at one corner of the bed through which a mosquito enters the net. It flies and sits at the diagonally opposite upper corner of the net. (a) Find the magnitude of the displacement of the mosquito. (b) Taking the hole as the origin, the length of the bed as the X-axis, it width as the Y axis, and vertically up as the Z-axis, write the components of the displacement vector.
Displacement vector of the mosquito,
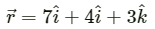
(a) Magnitude of displacement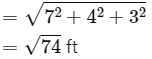
(b) The components of the displacement vector are 7 ft, 4 ft and 3 ft along the X, Y and Z-axes, respectively.
Q.10. Suppose 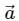 is a vector of magnitude 4.5 units due north. What is the vector (a)
is a vector of magnitude 4.5 units due north. What is the vector (a) 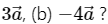
Given:
is a vector of magnitude 4.5 units due north.
Case (a):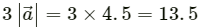
is a vector of magnitude 13.5 units due north.
Case (b):is a vector of magnitude 6 units due south.
Q.11. Two vectors have magnitudes 2 m and 3m. The angle between them is 60°. Find (a) the scalar product of the two vectors, (b) the magnitude of their vector product.
Let the two vectors be

Angle between the vectors, θ = 60°
(a) The scalar product of two vectors is given by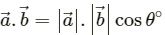
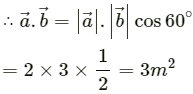
(b) The vector product of two vectors is given by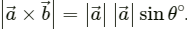
Q.12. Let A1 A2 A3 A4 A5 A6 A1 be a regular hexagon. Write the x-components of the vectors represented by the six sides taken in order. Use the fact the resultant of these six vectors is zero, to prove that cos 0 + cos π/3 + cos 2π/3 + cos 3π/3 + cos 4π/3 + cos 5π/3 = 0. Use the known cosine values to verify the result.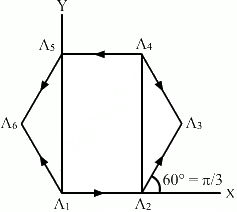
According to the polygon law of vector addition, the resultant of these six vectors is zero.
Here, a = b = c = d = e = f (magnitudes), as it is a regular hexagon. A regular polygon has all sides equal to each other.
So,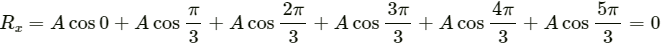
[As the resultant is zero, the x-component of resultant Rx is zero]Note: Similarly, it can be proven that
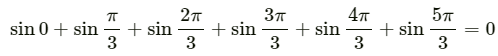
Q.13. Let 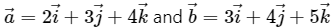 Find the angle between them.
Find the angle between them.
We have:
Using scalar product, we can find the angle between vectors
i.e.,
∴ The required angle is
Q.14. Prove that 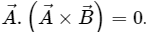
To prove:
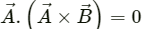
Proof: Vector product is given by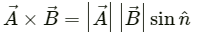
is a vector which is perpendicular to the plane containing
This implies that it is also perpendicular to
We know that the dot product of two perpendicular vectors is zero.
Hence, proved.
Q.15. If 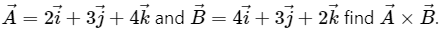
Given:
The vector product of
can be obtained as follows:
Q.16. If 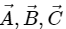 are mutually perpendicular, show that
are mutually perpendicular, show that 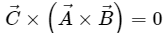 Is the converse true?
Is the converse true?
Given:
are mutually perpendicular.
is a vector with its direction perpendicular to the plane containing
∴ The angle betweenis either 0° or 180°.
i.e.,However, the converse is not true. For example, if two of the vectors are parallel, then also,

So, they need not be mutually perpendicular.
Q.17. A particle moves on a given straight line with a constant speed ν. At a certain time it is at a point P on its straight line path. O is a fixed point. Show that 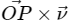 is independent of the position P.
is independent of the position P.
The particle moves on the straight line XX' at a uniform speed ν.
In
This product is always equal to the perpendicular distance from point O. Also, the direction of this product remains constant.
So, irrespective of the the position of the particle, the magnitude and direction ofremain constant.
is independent of the position P.
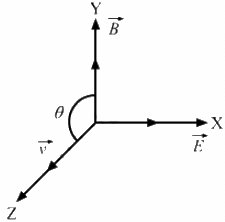
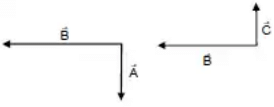
Q.18. The force on a charged particle due to electric and magnetic fields is given by 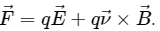 Suppose
Suppose 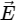 is along the X-axis and
is along the X-axis and 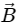 along the Y-axis. In what direction and with what minimum speed ν should a positively charged particle be sent so that the net force on it is zero?
along the Y-axis. In what direction and with what minimum speed ν should a positively charged particle be sent so that the net force on it is zero?
According to the problem, the net electric and magnetic forces on the particle should be zero.
i.e.,
So, the direction ofshould be opposite to the direction of
should be along the positive z-direction.
Again, E = νB sin θ
For ν to be minimum,
So, the particle must be projected at a minimum speed of E/B along the z-axis.
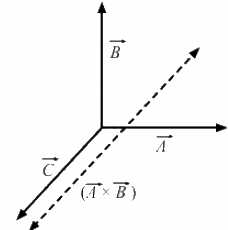
Q.19. Give an example for which 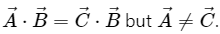
For example, as shown in the figure,

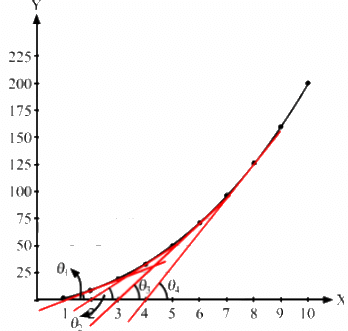
Q.20. Draw a graph from the following data. Draw tangents at x = 2, 4, 6 and 8. Find the slopes of these tangents. Verify that the curve draw is y = 2x2 and the slope of tangent is 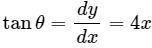
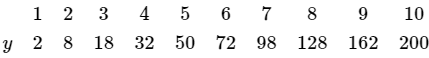
Note: Students should draw the graph y = 2x2 on a graph paper for results.
To find a slope at any point, draw a tangent at the point and extend the line to meet the x-axis. Then find tan θ as shown in the figure.
The above can be checked as follows:
Here, x = x-coordinate of the point where the slope is to be measured.
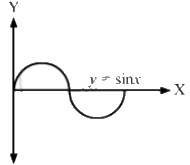
Q.21. A curve is represented by y = sin x. If x is changed from 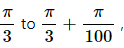 find approximately the change in y.
find approximately the change in y.
y = sin x ...(i)
Now, consider a small increment ∆x in x.
Then y + ∆y = sin (x + ∆x) ...(ii)
Here, ∆y is the small change in y.
Subtracting (ii) from (i), we get:
∆y = sin (x + ∆x) − sin x
= 0.0157
Q.22. The electric current in a charging R−C circuit is given by i = i0 e−t/RC where i0, R and C are constant parameters of the circuit and t is time. Find the rate of change of current at (a) t = 0, (b) t = RC, (c) t = 10 RC.
Given: i = i0 e−t/RC
∴ Rate of change of current
On applying the conditions given in the questions, we get:
Q.23. The electric current in a discharging R−C circuit is given by i = i0 e−t/RC where i0, R and C are constant parameters and t is time. Let i0 = 2⋅00 A, R = 6⋅00 × 105 Ω and C = 0⋅500 μF. (a) Find the current at t = 0⋅3 s. (b) Find the rate of change of current at at 0⋅3 s. (c) Find approximately the current at t = 0⋅31 s.
Electric current in a discharging R-C circuit is given by the below equation:
i = i0 ⋅ e−t/RC ...(i)
Here, i0 = 2.00 A
R = 6 × 105 Ω
C = 0.0500 × 10−6 F
= 5 × 10−7 F
On substituting the values of R, C and i0 in equation (i), we get:
i = 2.0 e−t/0.3 ...(ii)
According to the question, we have:
(a) current at t = 0.3 s
(b) rate of change of current at t = 0.3 s
(c) approximate current at t = 0.31 s
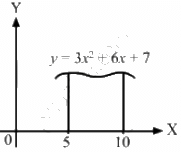
Q.24. Find the area bounded under the curve y = 3x2 + 6x + 7 and the X-axis with the ordinates at x = 5 and x = 10.
The given equation of the curve is y = 3x2 + 6x + 7.
The area bounded by the curve and the X-axis with coordinates x1 = 5 and x2 = 10 is given by
= 1135 sq. units.
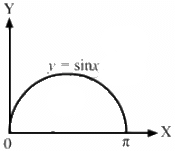
Q.25. Find the area enclosed by the curve y = sin x and the X-axis between x = 0 and x = π.
The given equation of the curve is y = sin x.
The required area can found by integrating y w.r.t x within the proper limits.
= 1 + 1 = 2 sq. unit
Q.26. Find the area bounded by the curve y = e−x, the X-axis and the Y-axis.
The given function is y = e−x.
When x = 0, y = e−0 = 1
When x increases, the value of y decrease. Also, only when x = ∞, y = 0
So, the required area can be determined by integrating the function from 0 to ∞.
Q.27. A rod of length L is placed along the X-axis between x = 0 and x = L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρ = a + bx. (a) Find the SI units of a and b. (b) Find the mass of the rod in terms of a, b and L.
ρ = mass/length = a + bx
So, the SI unit of ρ is kg/m.
(a)
SI unit of a = kg/m
SI unit of b = kg/m2
(From the principle of homogeneity of dimensions)
(b) Let us consider a small element of length dx at a distance x from the origin as shown in the figure given below:
dm = mass of the element
= ρdx
= (a + dx) dx
∴ Mass of the rod = ∫ dm
Q.28. The momentum p of a particle changes with time t according to the relation 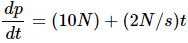 If the momentum is zero at t = 0, what will the momentum be at t = 10 s?
If the momentum is zero at t = 0, what will the momentum be at t = 10 s?
According to the question, we have:
Momentum is zero at time, t = 0
Now, dp = [(10 N) + (2 Ns−1)t]dt
On integrating the above equation, we get:
Q.29. The changes in a function y and the independent variable x are related as 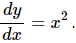 Find y as a function of x.
Find y as a function of x.
Changes in a function of y and the independent variable x are related as follows:
Integrating of both sides, we get:
where c is a constant
∴ y as a function of x is represented by.
Q.30. Write the number of significant digits in (a) 1001, (b) 100.1, (c) 100.10, (d) 0.001001.
(a) 1001
Number of significant digits = 4
(b) 100.1
Number of significant digits = 4
(c) 100.10
Number of significant digits = 5
(d) 0.001001
Number of significant digits = 4
Q.31. A metre scale is graduated at every millimetre. How many significant digits will be there in a length measurement with this scale?
The metre scale is graduated at every millimetre.
i.e., 1 m = 1000 mm
The minimum number of significant digits may be one (e.g., for measurements like 4 mm and 6 mm) and the maximum number of significant digits may be 4 (e.g., for measurements like 1000 mm). Hence, the number of significant digits may be 1, 2, 3 or 4.
Q.32. Round the following numbers to 2 significant digits.
(a) 3472, (b) 84.16. (c)2.55 and (d) 28.5
(a) In 3472, 7 comes after the digit 4. Its value is greater than 5. So, the next two digits are neglected and 4 is increased by one.
∴ The value becomes 3500.
(b) 84
(c) 2.6
(d) 29
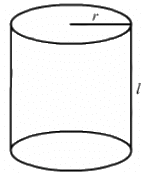
Q.33. The length and the radius of a cylinder measured with a slide callipers are found to be 4.54 cm and 1.75 cm respectively. Calculate the volume of the cylinder.
Length of the cylinder, l = 4.54 cm
Radius of the cylinder, r = 1.75 cm
Volume of the cylinder, V =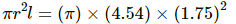
The minimum number of significant digits in a particular term is three. Therefore, the result should have three significant digits, while the other digits should be rounded off.
∴ Volume, V = πr2l
= (3.14) × (1.75) × (1.75) × (4.54)
= 43.6577 cm3
Since the volume is to be rounded off to 3 significant digits, we have:
V = 43.7 cm3
Q.34. The thickness of a glass plate is measured to be 2.17 mm, 2.17 mm and 2.18 mm at three different places. Find the average thickness of the plate from this data.
Average thickness
= 2 . 1733 mm
∴ Rounding off to three significant digits, the average thickness becomes 2.17 mm.
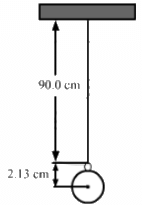
Q.35. The length of the string of a simple pendulum is measured with a metre scale to be 90.0 cm. The radius of the bod plus the length of the hook is calculated to be 2.13 cm using measurements with a slide callipers. What is the effective length of the pendulum? (The effective length is defined as the distance between the point of suspension and the centre of the bob.)
Consider the figure shown below:
Actual effective length = (90.0 + 2.13) cm
However, in the measurement 90.0 cm, the number of significant digits is only two.
So, the effective length should contain only two significant digits.
i.e., effective length = 90.0 + 2.13 = 92.1 cm.
|
134 docs
|