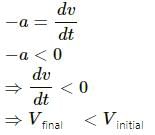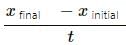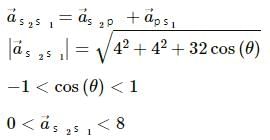Short Answers
Q.1. Galileo was punished by the Church for teaching that the sun is stationary and the earth moves around it. His opponents held the view that the earth is stationary and the sun moves around it. If the absolute motion has no meaning, are the two viewpoints not equally correct or equally wrong?
The absolute motion has no meaning. In the relative motion view, the two viewpoints are the same. Hence, both viewpoints are equally correct or equally wrong.
Q.2. When a particle moves with constant velocity, its average velocity, its instantaneous velocity and its speed are all equal. Comment on this statement.
Constant velocity means that a particle has the same direction and speed at every point. So, its average velocity and instantaneous velocity are equal. Its speed being a scalar quantity is equal in magnitude only.
Q.3. A car travels at a speed of 60 km/hr due north and the other at a speed of 60 km/hr due east. Are the velocities equal? If no, which one is greater? If you find any of the questions irrelevant, explain.
No, as the directions of the cars are different, their velocities are not equal, as velocity is a vector quantity.
We cannot compare velocities on the basis of direction only, so the question is irrelevant.
Q.4. A ball is thrown vertically upward with a speed of 20 m/s. Draw a graph showing the velocity of the ball as a function of time as it goes up and then comes back.

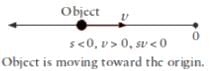
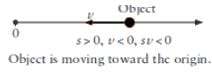
Q.5. The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion.
Motion of a projectile at the highest point of its path: Because at this point, the projectile has only horizontal component of velocity. So, it can have velocity towards west and acceleration in the vertically downward direction.
Q.6. At which point on its path a projectile has the smallest speed?
A projectile has the lowest speed at the highest point of its path because the vertical component of velocity is zero at this point.
Q.7. Two particles A and B start from rest and move for equal time on a straight line. The particle A has an acceleration a for the first half of the total time and 2a for the second half. The particle B has an acceleration 2a for the first and a for the second half. Which particle has covered larger distance?
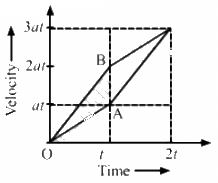
From the velocity–time graph, we have:
Distance covered by A = 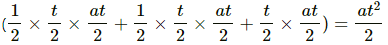
Distance covered by B = 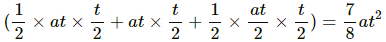
∴ Distance covered by A < Distance covered by B
Q.8. If a particle is accelerating, it is either speeding up or speeding down. Do you agree with this statement?
Acceleration does not mean speeding up or speeding down. It means the change of velocity either in direction or in magnitude.
Q.9. A food packet is dropped from a plane going at an altitude of 100 m. What is the path of the packet as seen from the plane? What is the path as seen from the ground ? If someone asks "what is the actual path", what will you answer?
The path of the packet (as seen from the plane) is a vertically downward straight line, as the horizontal velocity of the packet and the plane is the same.
As seen from the ground, the path of the packet is a parabola.
The path is defined with respect to some reference frame. As there is no absolute reference frame, no actual path is defined.
Q.10.1. Give example where the velocity of a particle is zero but its acceleration is not zero.
At the highest point when a particle is thrown vertically upwards.
Q.10.2. Give example where the velocity is opposite in direction to the acceleration.
While going up when a particle is thrown vertically upwards.
Q.10.3. Give example where the velocity is perpendicular to the acceleration.
At the highest point of a full projectile.
Q.11. In figure shows the x coordinate of a particle as a function of time. Find the sings of vx and ax at t = t1, t = t2 and t = t3.
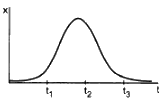
Slope of the x–t graph gives the velocity and change in the slope gives the acceleration.
At t = t1,
Slope = Positive ⇒ Velocity = Positive
Slope is increasing ⇒ Acceleration = Positive
At t = t2,
Slope = Constant ⇒ Velocity = Zero
Slope is constant ⇒ Acceleration = Negative
At t = t3,
Slope = Negative ⇒ Velocity = Negative
Slope is increasing ⇒ Acceleration = Negative
Q.12. A player hits a baseball at some angle. The ball goes high up in space. The player runs and catches the ball before it hits the ground. Which of the two (the player or the ball) has greater displacement?
The displacement of the ball and the player is the same, as the initial and final points are the same.
Q.13. The increase in the speed of a car is proportional to the additional petrol put into the engine. Is it possible to accelerate a car without putting more petrol or less petrol into the engine?
Yes, it is possible to accelerate a car without putting more petrol or less petrol in the engine. This can be done by driving the car on a circular or curved track at a uniform speed.
Q.14. Rain is falling vertically. A man running on the road keeps his umbrella tilted but a man standing on the street keeps his umbrella vertical to protect himself from the rain. But both of them keep their umbrella vertical to avoid the vertical sun-rays. Explain.
The speed of rain is less, so as we run, the direction of the relative velocity of the rain changes. But as the speed of light is very high, there is a measurable change in the relative velocity of light w.r.t. a person due to the relative motion between the sunrays and the person.
Multiple Choice Questions
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
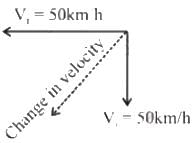
Try yourself:A motor car is going due north at a speed of 50 km/h. It makes a 90° left turn without changing the speed. The change in the velocity of the car is about
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:In figure shows the displacement-time graph of a particle moving on the X-axis.
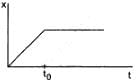
Explanation
The slope of the x–t graph gives the velocity. In the graph, the slope is constant from t = 0 to t = t0, so the velocity is constant. After t = t0, the displacement is zero; i.e., the particle stops.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:A particle has a velocity u towards east at t = 0. Its acceleration is towards west and is constant. Let xA and xB be the magnitude of displacements in the first 10 seconds and the next 10 seconds
Explanation
As velocity and acceleration are in opposite directions, velocity will become zero after some time (t) and the particle will return.
Because the value of acceleration is not given, we cannot say that the particle will return after/before 10 seconds.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
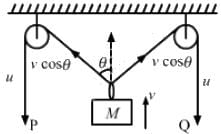
Try yourself:In the arrangement shown in figure the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass M moves upwards with a speed
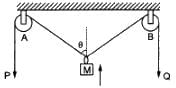
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:A person travelling on a straight line moves with a uniform velocity v1 for some time and with uniform velocity v2 for the next equal time. The average velocity v is given by
Explanation
Velocity is uniform in both cases; that is, acceleration is zero.
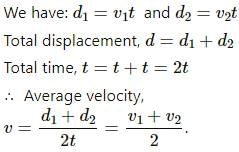
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:A person travelling on a straight line moves with a uniform velocity v1 for a distance x and with a uniform velocity v2 for the next equal distance. The average velocity v is given by
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:A stone is released from an elevator going up with an acceleration a. The acceleration of the stone after the release is
Explanation
Gravity is the only force acting on the stone when it is released. And, we know that gravity is always in the downward direction.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:A person standing near the edge of the top of a building throws two balls A and B. the ball A is thrown vertically upward and B is thrown vertically downward with the same speed. The ball A hits the ground with a speed vA and the ball B this the ground with a speed vB. We have
Explanation
Total energy of any particle = 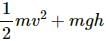
Both the particles were at the same height and thrown with equal initial velocities, so their initial total energies are equal. By the law of conservation of energy, their final energies are equal.
At the ground, they are at the same height. So, their P.E. are also equal; this implies that their K.E. should also be equal. In other words, their final velocities are equal.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:In a projectile motion the velocity
Explanation
In projectile motion, velocity is perpendicular to acceleration only at the highest point. Here, velocity is along the horizontal direction and acceleration is along the vertically downward direction.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:Two bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit he ground first?
Explanation
Because the downward acceleration and the initial velocity in downward direction of the two bullets are the same, they will take the same time to hit the ground and for a half projectile.
Time of flight = T = 
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:The range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be
Explanation
For the same u range, 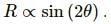
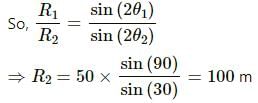
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:Two projectiles A and B are projected with angle of projection 15° for the projectile A and 45° for the projectile B. If RA and RB be the horizontal range for the two projectiles, then
Explanation
Horizontal range for the projectile, 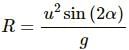 Information of the initial velocity is not given in the question
Information of the initial velocity is not given in the question
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:A river is flowing from west to east at a speed of 5 metres per minute. A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction.
Explanation
If the man swims at any angle east to the north direction, although his relative speed will increase, he will have to travel a larger distance. So, he will take more time.
If the man swims at any angle west to the north direction, his relative speed will decrease. So, he will take more time.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:Consider the motion of the tip of the minute hand of a clock. In one hour
Explanation
(a) the displacement is zero
(d) the average velocity is zero
Displacement is zero because the initial and final positions are the same.
Average velocity = Displacement/Total time = 0
Distance covered = 2πr ≠ 0
Average speed = Distance travelled/Total time taken ≠ 0
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:A particle moves along the X-axis as x = u (t − 2 s) + a (t − 2 s)2.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:Pick the correct statements:
Explanation
(a) Average speed of a particle in a given time is never less than the magnitude of the average velocity.
(b) It is possible to have a situation in which 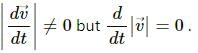
(c) The average velocity of a particle is zero in a time interval. It is possible that the instantaneous velocity is never zero in the interval, for example, the motion of a particle on a circular track with a constant speed.
Average velocity = Displacement/ Total time
Displacement ≤ Distance
∴ Average velocity ≤ Average speed In uniform circular motion, speed is constant but velocity is not.
i.e., 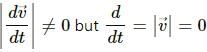 which proves case (b)
which proves case (b)
(d) In one complete circle of uniform motion, average velocity is zero. Instantaneous velocity is never zero in the interval.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:An object may have
Explanation
(b) varying velocity without having varying speed
(d) nonzero acceleration without having varying speed
Velocity and acceleration are vector quantities that can be changed by changing direction only (keeping magnitude constant).
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:Mark the correct statements for a particle going on a straight line:
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:The velocity of a particle is zero at t = 0.
Explanation
(b) The acceleration at t = 0 may be zero.
(c) If the acceleration is zero from t = 0 s to t = 10 s, the speed is also zero in this interval.
(d) If the speed is zero from t = 0 s to t = 10 s, the acceleration is also zero in this interval.
(b) Acceleration will be zero only when the change in velocity is zero.
(c) Since the acceleration is zero from t = 0 s to t = 10 s, change in velocity is 0.
Velocity in this interval = Initial velocity = 0
Also,
Speed in this interval = Initial speed = 0
(d) From t = 0 s to t = 10 s, speed is zero.
Here, velocity is zero and initial velocity is zero.
So, the change in velocity is zero; i.e., acceleration is zero.
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:Mark the correct statements:
Explanation
The magnitude of the velocity of a particle is equal to its speed.
(a) Velocity being a vector quantity has magnitude as well as direction, and magnitude of velocity is called speed.
(b) Average velocity = Total displacement/Total time taken
Average speed = Total distance travelled/Total time taken
Distance ≥ Displacement
∴ Average speed ≥ Average velocity
The magnitude of average velocity in an interval is not always equal to its average speed in that interval.
(c) If speed is always zero, then the distance travelled is always zero. Hence, the total distance travelled and the average speed will be zero.
(d) If the speed of a particle is never zero, the distance travelled by the particle is never zero. Hence, the average speed will not be zero.
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
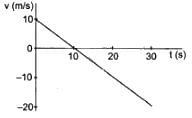
Try yourself:The velocity-time plot for a particle moving on a straight line is shown in the figure.
Explanation
(a) The particle has a constant acceleration.
(d) The average speed in the interval 0 s to 10 s is the same as the average speed in the interval 10 s to 20 s.
Explanation:
(a) The slope of the v–t graph gives the acceleration. For the given graph, the slope is constant. So, acceleration is constant.
(b) From 0 to 10 seconds, velocity is in positive direction and then in negative direction. This means that the particle turns around at t = 10 s.
(c) Area in the v–t curve gives the distance travelled by the particle.
Distance travelled in positive direction ≠ Distance travelled in negative direction
∴ Displacement ≠ Zero
(d) The area of the v–t graph from t = 0 s to t = 10 s is the same as that from t = 10 s to t= 20 s. So, the distance covered is the same. Hence, the average speed is the same.
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:In figure shows the position of a particle moving on the X-axis as a function of time.

Explanation
The particle has come to rest 6 times.
Explanation:
(a) The slope of the x–t graph gives the velocity. Here, 6 times the slope is zero. So, the particle has come to rest 6 times.
(b) As the slope is not maximum at t = 6 s, the maximum speed is not at t = 6 s.
(c) As the slope is not positive from t = 0 s to t = 6s, the velocity does not remain positive.
(d) Average velocity = Total displacement/Total time taken
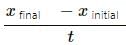
For the shown time (t = 6 s), the displacement of the particle is positive. Therefore, the average velocity is positive.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 3- Rest and Motion: Kinematics- 1
Try yourself:The accelerations of a particle as seen from two frames S1 and S2 have equal magnitude 4 m/s2.
Explanation
The acceleration of S2 with respect to S1 may be anything between zero and 8 m/s2.
Explanation:
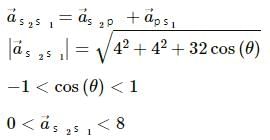
Report a problem













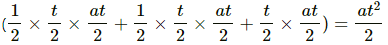
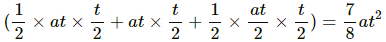
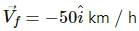 Initial velocity,
Initial velocity, 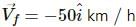 Change in velocity,
Change in velocity, 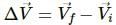
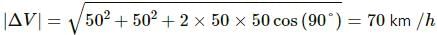
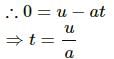
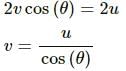
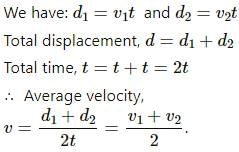
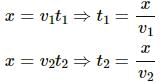
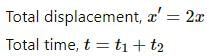
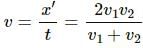
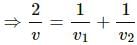
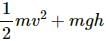

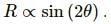
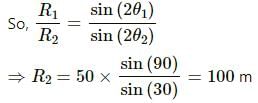
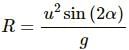 Information of the initial velocity is not given in the question
Information of the initial velocity is not given in the question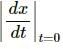
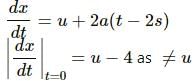
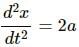
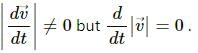
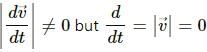 which proves case (b)
which proves case (b)