Notes: Sphere | Mathematics for Grade 10 PDF Download
| Table of contents |

|
| Introduction |

|
| What is a Sphere? |

|
| Shape of Sphere |

|
| Properties of a Sphere |

|
| Equation of a Sphere |

|
| Sphere Formulas |

|
| Surface Area of a Sphere |

|
| Volume of a Sphere |

|
Introduction
A sphere is a three-dimensional object that is round in shape. The sphere is defined in three axes, i.e., x-axis, y-axis and z-axis. This is the main difference between circle and sphere. A sphere does not have any edges or vertices, like other 3D shapes.
The points on the surface of the sphere are equidistant from the center. Hence, the distance between the center and the surface of the sphere are equal at any point. This distance is called the radius of the sphere. Examples of spheres are a ball, a globe, the planets, etc.
What is a Sphere?
As discussed in the introduction, the sphere is a geometrical figure that is round in shape. The sphere is defined in a three-dimensional space. The sphere is three dimensional solid, that has surface area and volume. Just like a circle, each point of the sphere is at an equal distance from the center.
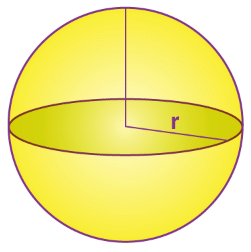 In the above figure, we can see, a sphere with radius ‘r’.
In the above figure, we can see, a sphere with radius ‘r’.
Unlike a circle, which is a plane shape or flat shape, defined in XY plane, a sphere is defined in three dimensions, i.e. x-axis, y-axis and z-axis.
Important Facts on Sphere
- A sphere is a symmetrical object
- All the surface points of the sphere are equidistant from center
- A sphere has an only a curved surface, no flat surface, no edges and no vertices
Shape of Sphere
The shape of a sphere is round and it does not have any faces. The sphere is a geometrical three-dimensional solid having a curved surface. Like other solids, such as cube, cuboid, cone and cylinder, a sphere does not have any flat surface or a vertex or an edge.
The real-life examples of the sphere are:
- Basketballs
- World Globe
- Marbles
- Planets
- Moon
Properties of a Sphere
The important properties of the sphere are given below. These properties are also called attributes of the sphere.
- A sphere is perfectly symmetrical
- A sphere is not a polyhedron
- All the points on the surface are equidistant from the center
- A sphere does not have a surface of centers
- A sphere has constant mean curvature
- A sphere has a constant width and circumference.
Equation of a Sphere
In analytical geometry, if “r” is the radius, (x, y, z) is the locus of all points and (x0, y0, z0) is the center of a sphere, then the equation of a sphere is given by:
(x -x0)2 + (y – y0)2 + (z-z0)2 = r2
Sphere Formulas
The common formulas of the sphere are:
- Surface area
- Volume
Diameter of sphere D = 2r, where r is the radius
Surface area of sphere SA = 4πr2 Square units
Volume of sphere V = 4/3 πr3 Cubic Units
Surface Area of a Sphere
The surface area of a sphere is the total area covered by the surface of a sphere in a three-dimensional space. The formula of surface are is given by:
The Surface Area of a Sphere(SA) = 4πr2 Square units
Where “r” is the radius of the sphere.
Volume of a Sphere
The amount of space occupied by the object three-dimensional object called a sphere is known as the volume of the sphere.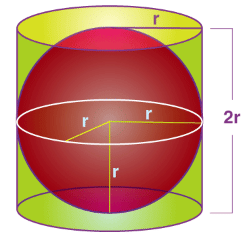
According to the Archimedes Principle, the volume of a sphere is given as,
The volume of Sphere(V) = 4/3 πr3 Cubic Units
Difference Between a Sphere and a Circle
A circle and a sphere are shapes in geometry, that appear the same, but are different in properties. The key differences between the two shapes are listed below in the table.
Solved Example
Example 1: Find the volume of the sphere that has a diameter of 10 cm?
Given, Diameter, d = 10 cm
We know that D = 2 r units
Therefore, the radius of a sphere, r = d / 2 = 10 / 2 = 5 cm
To find the volume:
The volume of sphere = 4/3 πr3 Cubic Units
V = (4/3)× (22/7) × 53
Therefore, the volume of sphere, V = 522 cubic units
Example 2: Determine the surface area of a sphere having a radius of 7 cm.
Given radius = 7 cm
The Surface Area of a Sphere(SA) = 4πr2 Square units
SA = 4× (22/7)× 72
SA = 4 × 22 × 7
SA = 616 cm2
Therefore, the surface area of a sphere = 616 square units.
Example 3: Find the volume of a sphere in terms of π, if the radius is 9 cm?
Given: Radius, r = 9 cm.
We know that the volume of a sphere is 4/3 πr3 Cubic Units
Now, substitute r = 9 in the formula, we get
V = (4/3)× π × 9 × 9 × 9 cm3
V = 4 × π × 3 × 9 × 9 cm3
V = 972 π cm3
Hence, the volume of a sphere is 972 cubic centimeters, if the radius is 9 cm.
|
137 videos|83 docs|44 tests
|















