Reflection, Rotation & Translation | Mathematics for Grade 10 PDF Download
| Table of contents |

|
| Reflection |

|
| The Equation of the Line of Symmetry |

|
| Rotation |

|
| Different Centres of Rotation |

|
| Translation |

|
| Describing Translations |

|
Reflection
- A shape can be reflected across a line of reflection to create an image.
- The line of reflection is also called the mirror line.
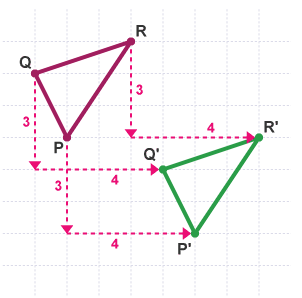
- The triangle PQR has been reflected in the mirror line to create the image P'Q'R'.
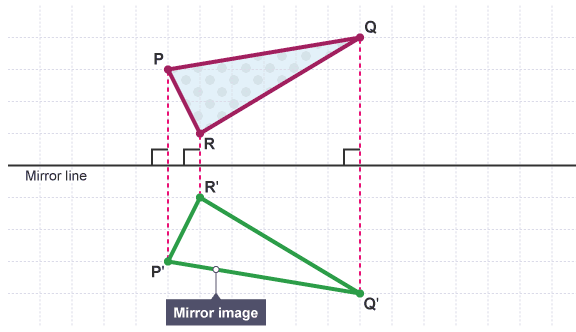
- Reflection is an example of a transformation. A transformation is a way of changing the size or position of a shape.
- Every point in the image is the same distance from the mirror line as the original shape.
- The line joining a point on the original shape to the same point on the image is perpendicular to the mirror line.
For example, the line between R and R' is perpendicular to the mirror line.
The Equation of the Line of Symmetry
To describe a reflection on a grid, the equation of the mirror line is needed.
Example:
Reflect the shape in the line x = -1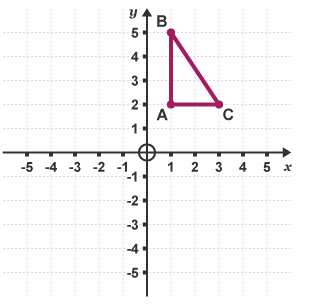
The line x = -1 is a vertical line which passes through -1 on the x-axis.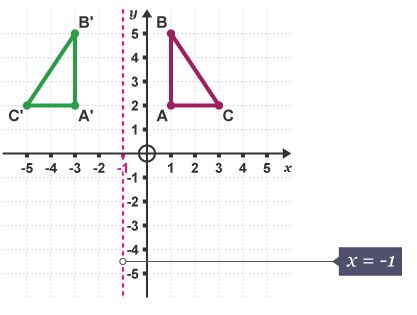
Solved Example
Example 1: Describe the transformation of the shape ABC.
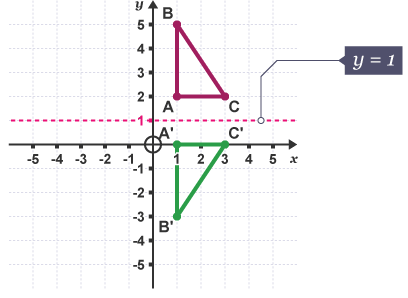
The line y = 1 is a horizontal line which passes through 1 on the y-axis.
The shape is a reflection in the line y = 1.
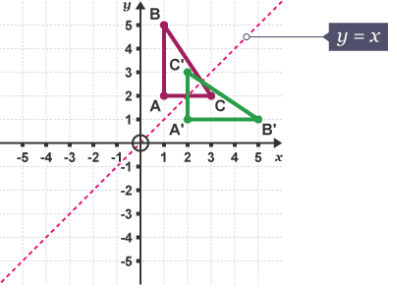
Example 2: Reflect the shape in the line y = x.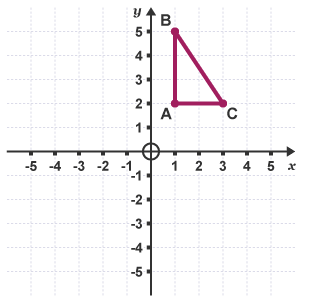
The equation of a straight line graph has the form y = mx + c, where m is the gradient and is where the line crosses the y-axis.
The line y = x passes through points that have the same and coordinates, eg (0, 0), (1, 1), (2, 2).
Example 3: Describe the transformation of the shape ABC.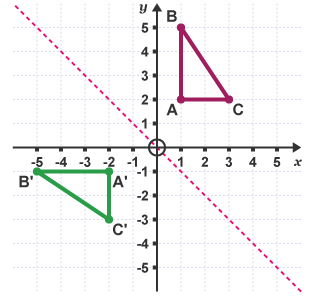
The mirror line has a gradient of -1 and crosses the y-axis at (0,0).
The shape is a reflection in the line.
Note: The equation of the mirror line is needed to fully describe a reflection.
Rotation
Rotation turns a shape around a fixed point called the centre of rotation.
Rotation is an example of a transformation. A transformation is a way of changing the size or position of a shape.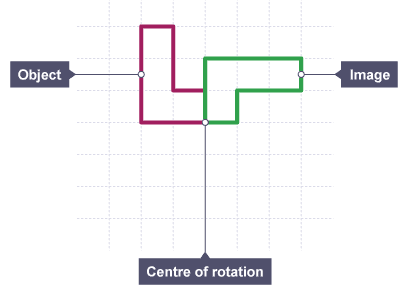
The shape has been rotated 90° (a quarter turn) clockwise about the centre of rotation
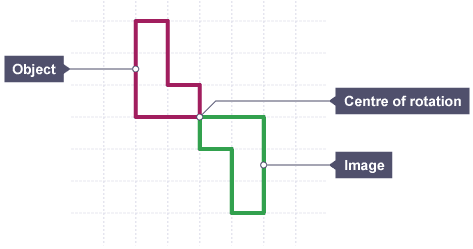
The shape has been rotated 180° (a half-turn) about the centre of rotation

The shape has been rotated 90° (a quarter turn) anticlockwise about the centre of rotation
Three pieces of information are needed to rotate a shape:
- the centre of rotation
- the angle of rotation
- the direction of rotation
The triangle PQR has been rotated 90° anticlockwise about the origin O to create the image P'Q'R'.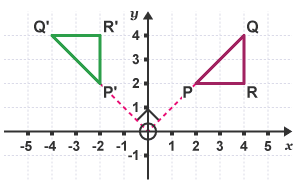
Example:
Rotate the triangle PQR 90° anticlockwise about the origin. Tracing paper can be used to rotate a shape.
Tracing paper can be used to rotate a shape.
Trace the shape and the centre of rotation.
Hold down the tracing paper with a pencil on the centre of rotation.
Rotate the tracing paper and copy the image.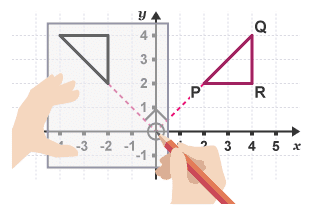
Solved Example
Example 1: Describe the transformation of the rectangle ABCD.
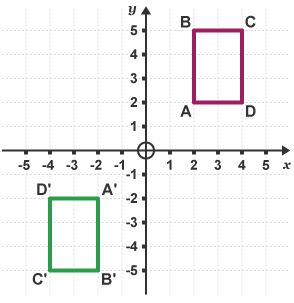
Each vertex of the image A'B'C'D' is the same distance from the origin as the original shape. The origin is the centre of rotation.
The rectangle ABCD has been rotated 180° about the origin (the direction is not required because it can be either clockwise or anticlockwise).
Different Centres of Rotation
The centre of rotation may not be at the origin.
Example:
Rotate the rectangle ABCD 90° clockwise about the point (0,-1).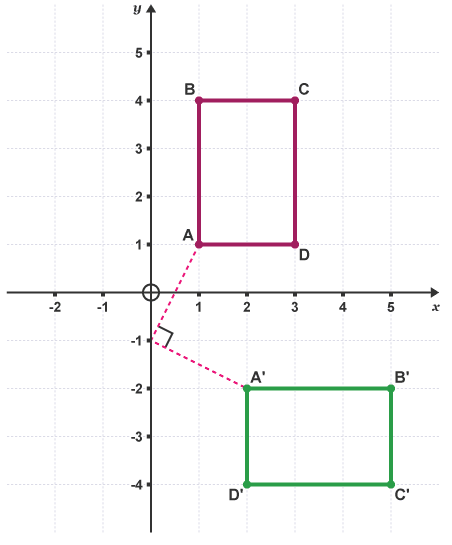
Each corner of the image A'B'C'D' is the same distance from the centre of rotation as the original shape.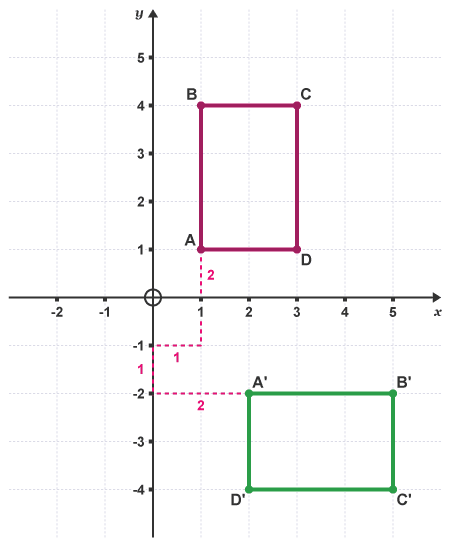
Translation
- A translation moves a shape up, down or from side to side but it does not change its appearance in any other way.
- Translation is an example of a transformation. A transformation is a way of changing the size or position of a shape.
- Every point in the shape is translated the same distance in the same direction.
Describing Translations
Column vectors are used to describe translations.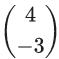 means translate the shape 4 squares to the right and 3 squares down.
means translate the shape 4 squares to the right and 3 squares down.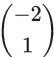 means translate the shape 2 squares to the left and 1 square up.
means translate the shape 2 squares to the left and 1 square up.
Vectors are given in the form
where x is the movement horizontally and y is the movement vertically. A positive value of x means a movement to the right and a negative value of x means a movement to the left. A positive value of y means a movement upwards and a negative value of y means a movement downwards.
Example: Describe the transformation of the shape DEFG.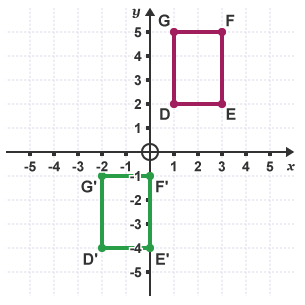
The shape has been translated by the vector 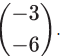 The shape has moved three units to the left and six units down.
The shape has moved three units to the left and six units down.
|
137 videos|83 docs|44 tests
|