Notes: Congurent & Similar Shapes | Mathematics for Grade 10 PDF Download
| Table of contents |

|
| Congruent Shapes |

|
| Congruent Triangles |

|
| Similar Shapes |

|
| Similar Triangles |

|
| Lengths, Areas and Volumes of Similar Shapes - Higher |

|
| Ratio of Volumes |

|
Congruent Shapes
Two shapes that are the same size and the same shape are congruent.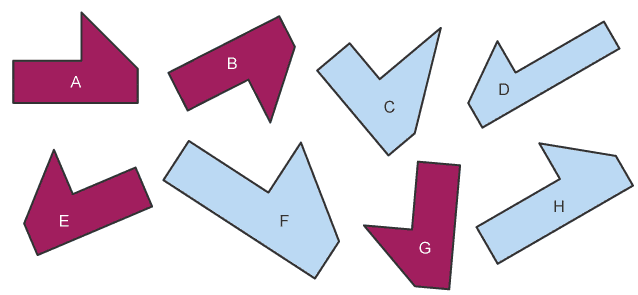
Shapes A, B, E and G are congruent. They are identical in size and shape.
Congruent Triangles
For two triangles to be congruent, one of 4 criteria need to be met.
The three sides are equal (SSS: side, side, side) Two angles are the same and a corresponding side is the same (AA corr S: angle, angle, corresponding side)
Two angles are the same and a corresponding side is the same (AA corr S: angle, angle, corresponding side)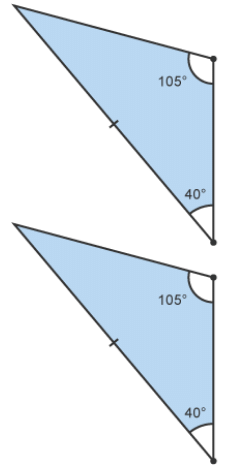 Two sides are equal and the angle between the two sides is equal (SAS: side, angle, side)
Two sides are equal and the angle between the two sides is equal (SAS: side, angle, side)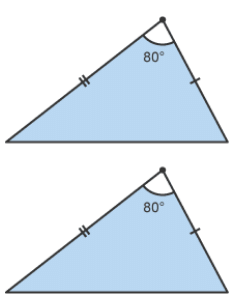
A right angle, the hypotenuse and a corresponding side are equal (RHS, right angle, hypotenuse, side)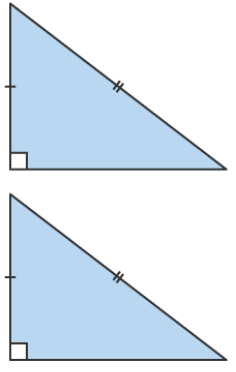
Example 1: State whether the two triangles are congruent. Give a reason to support your answer.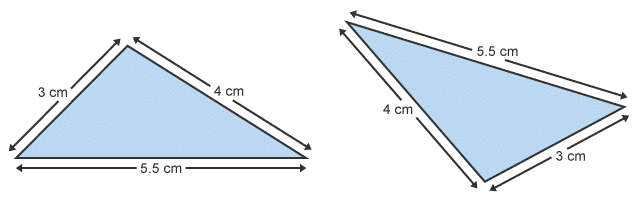
Yes - SSS, the three sides are equal.
Example 2: State whether the two triangles are congruent. Give a reason to support your answer.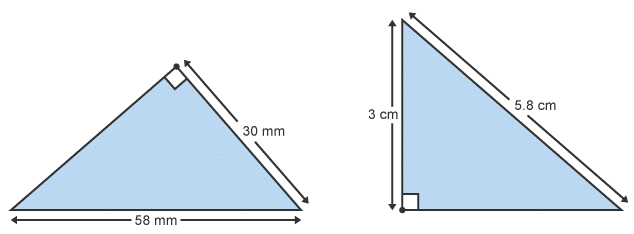
Yes - RHS.
Solved Example
Example 1: State whether the two triangles are congruent. Give a reason to support your answer.
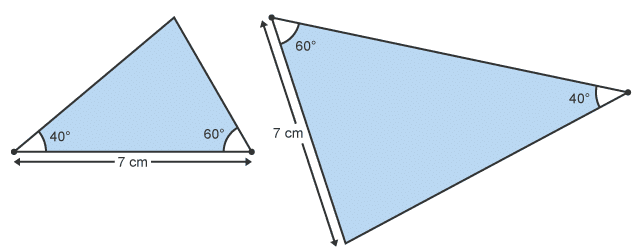
No - in the left hand diagram the 7 cm length is between the angles 40° and 60°. In the right hand diagram it is not.
Similar Shapes
When a shape is enlarged, the image is similar to the original shape. It is the same shape but a different size.
These two shapes are similar as they are both rectangles but one is an enlargement of the other.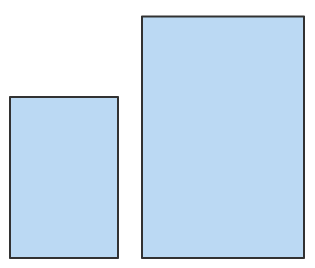
Similar Triangles
Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. Either of these conditions will prove two triangles are similar.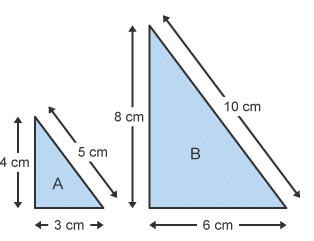
Triangle B is an enlargement of triangle A by a scale factor of 2. Each length in triangle B is twice as long as in triangle A.
The two triangles are similar.
Example 1: State whether the two triangles are similar. Give a reason to support your answer.
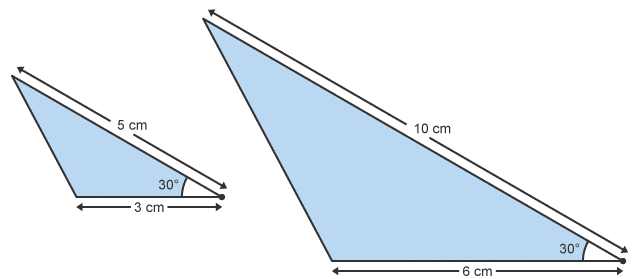
Yes, they are similar. The two lengths have been increased by a scale factor of 2. The corresponding angle is the same.
Example 2: State whether the two triangles are similar. Give a reason to support your answer.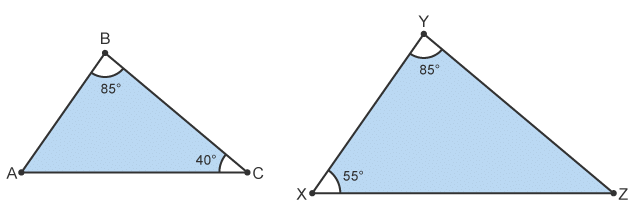
To decide whether the two triangles are similar, calculate the missing angles.
Remember angles in a triangle add up to 180°.
Angle BAC = 180° - 85° - 40° = 55°
Angle YZX = 180° - 85° - 40° = 40°
Yes, they are similar. The three angles are the same.
Example 3: State whether the two triangles are similar. Give a reason to support your answer.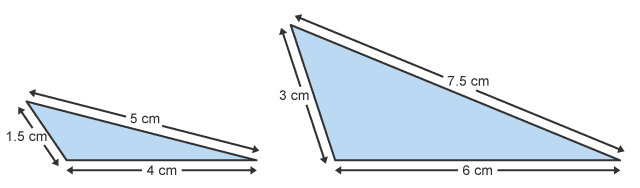 No. The two sides of the triangle are increased by a scale factor of 1.5. The other side has been increased by a scale factor of 2.
No. The two sides of the triangle are increased by a scale factor of 1.5. The other side has been increased by a scale factor of 2.
Calculating lengths and angles in similar shapes
In similar shapes, the corresponding lengths are in the same ratio. This fact can be used to calculate lengths.
Example: Calculate the length PS.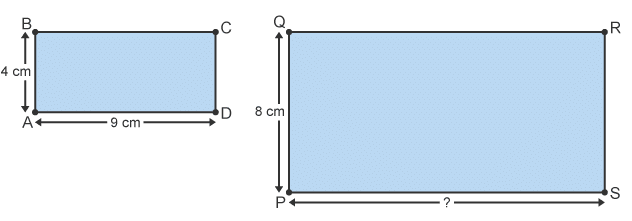 The scale factor of enlargement is 2.
The scale factor of enlargement is 2.
Length PS is twice as long as length AD.
PS = 9 x 2 = 18 cm
Similar shapes may be inside one another.
Solved Example
Example 1: Show that triangles ABC and DBE are similar and calculate the length DE.
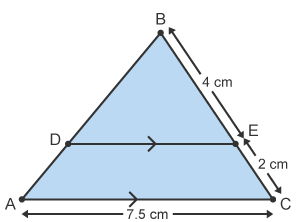
Angle BCA = angle BED because of corresponding angles in parallel lines.
Angle BAC = angle BDE because of corresponding angles in parallel lines.
Angle DBE = angle ABC because both triangles share the same angle.
All three angles are the same in both triangles so they are similar.
To calculate a missing length, draw the two triangles separately and label the lengths.
To calculate the scale factor, divide the two corresponding lengths.
6/4 = 1.5
The scale factor of enlargement is 1.5.
DE = 7.5 ÷ 1.5 = 5 cm
Example 2: Triangles QST and QPR are similar.
Calculate the length TR.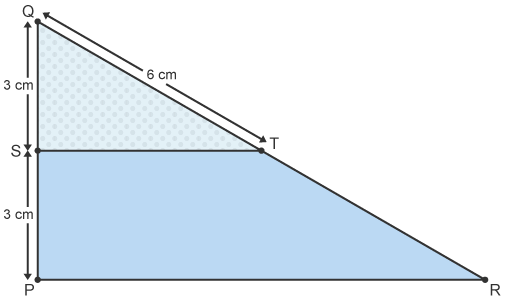
To calculate a missing length, draw the two triangles separately and label the lengths.
The scale factor is 6/3 = 2
To calculate TR, first find QR.
QR = 6 x 2 = 12 cm
QR = QT + TR
TR = QR - QT
TR = 12 - 6 = 6 cm
Lengths, Areas and Volumes of Similar Shapes - Higher
Ratio of Areas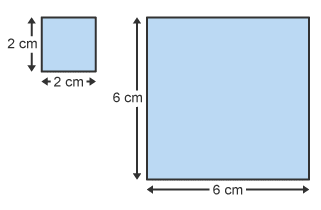
The lengths of the larger square are 3 times the lengths of the smaller square.
The scale factor is 3.
The area of the smaller square is 4 cm2. The area of the larger square is 36 cm2.
The area of the larger square is 9 times larger than the area of the smaller square.
The ratio of areas is . This is 1 : 9. This is 1 : 32
If the scale factor is k, the ratio of areas is k2.
Example: These two clocks are similar. The area of the small clock face is approximately 28.3 cm2. Calculate the area of the face of the larger clock.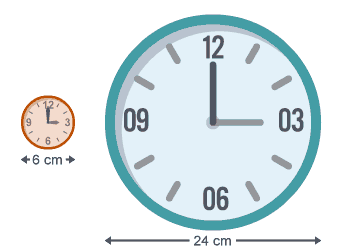 The scale factor = 24/6 = 4
The scale factor = 24/6 = 4
The ratio of areas is = 1 : 42 = 1 : 16
28.3 x 16 = 452.8
The area of the large clock face is approximately 452.8 cm2.
Solved Example
Example: These two pieces of paper are similar. The area of an A3 piece of paper is double the area of an A4 piece of paper. Calculate the width of the smaller piece of paper.
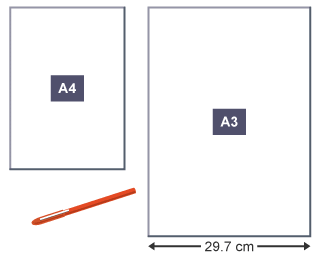
The ratio of areas is 1 : 2. The ratio of lengths is 1 : √2
In this case, the scale factor is √2.
Smaller length = larger length ÷ √2
29.7 ÷ √2 = 21 cm
Ratio of Volumes
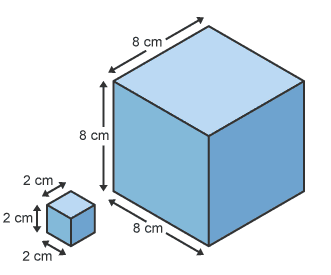
The lengths of the larger square are 4 times the lengths of the smaller square.
The scale factor is 4.
The volume of the smaller cube is 8 cm3.
The volume of the larger cube is 512 cm3.
The ratio of volumes is 8 : 512 = 1 : 64. This is 1 : 43
If the scale factor is k, the ratio of volumes is k3.
Example: These two tins of soup are similar. Calculate the diameter of the larger tin of soup.
The ratio of volumes is 125 : 500 = 1 : 4
The ratio of lengths is 1 : ∛4
The scale factor is: ∛4
Larger diameter = smaller diameter x ∛4
5 x ∛4 = 7.9 cm (1 dp)
|
138 videos|100 docs|44 tests
|



















